Random Processes (2)

뿌아송~

• 오늘 배울 것은 Poisson process로 BP에서 Continous한 상황을 생각한 방식이다.

Poisson Processes : Poisson RV and Basic Idea

Background : Poisson rv X with parameter λ (1)

• 예전에 배웠던 Binomial RV에 대해 생각해보면 이 놈의 정의는 다음과 같다.
  → n번의 독립적인 시도에서 성공확률 p를 가질 때, 성공 개수
  → Models the number of successes in a given number n of independent trials with success probability p.

• 공식은 다음과 같다.
  

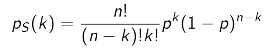
• 여기서 우리는 궁금해진 것이 있다.
  → 매우매우 큰 n과 매우 작은 p를 가지고 np = λ로 정했을 때, 어떤 일이 발생할까?
  → 즉, np = λ를 가정하고 n이 무한대로 갈 때 어떻게 될까?

  • 여기서 np = λ는 쉽게 생각하면 된다.
    1. n = 1일 때, p = λ
    2. n = 2일 때, p = λ/2
    3. n = n일 때, p = λ/n

• 앞서 나온 공식을 np = λ를 적용해서 lim하기 쉽게 풀게 되면
  
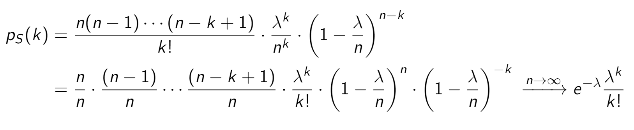
  → 요놈이 Poisson rv이다.
  

  
  

Background : Poisson rv X with parameter λ (2)

• 앞서 찾아낸 Poisson rv의 공식은 다음과 같다.
  

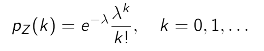
  1. 기본적으로 Binomail을 표방했기 때문에, λ는 nonnegative integer value를 갖는다.
  2. Infinitely many slots(n) with the infinitely small slot duration

• Poisson rv의 Expectation과 var은 다음과 같다.
  
  

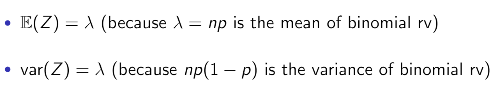
  → 여기서 Expectation은 mean # of arrivals이다.
  → var을 구할 때, np(1-p)에서 n이 무한대로 갈 때를 생각하며 된다.
  
  

Example : Poisson Approximation

• Limit을 취하기 때문에 Approximation이라고 하기도 한다.

• 요놈자식이 어디에 쓰이는지 하나의 예제를 살펴보자.

  A packet consisting of a string of n symbols is transmitted over a noisy channel.

  Each symbol has errorneous transmission with prob. of 0.0001, independent of other symbols.

  Incorrect transmission is when at least one symbol is in error.

  
  Question. How small should n be in order for the prob. of incorrect transmission to be less than 0.001?

• 에러 확률은 아주 낮다. 그리고 패킷의 길이가 꽤나 크다.
  → Poisson approximation을 사용하자!

• 간단하다.
  

  

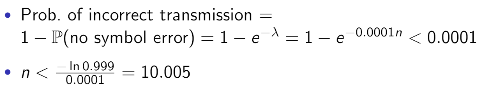
Design of Continuous Analogue of Bernoulli Process

• Remind
  • Geometric vs. Exponential
  • Two rvs with memoryless property
  • conitnuous system is discrete system with infinitely many slots whose duration is infinitely small.
• Independence between what happens in a different time region.
• Memoryless and fresh-start property
• Key Idea : Making it as a limit of a sequence of Bernoulli processes.

Key design idea to develop a Continuous Twin (1)

• Continuous twin

  • Key point : Understand the number of arrivals over a given interval [0, 𝛕]

  • Assume that it has some arrival rate λ.
    

    → Bern Process에서 하나의 슬롯에서의 성공확률 p를 모방한 것
    → # of arrivals / unit time

  • 우리는 discrete time slots의 BP를 다룰 줄 안다.

• Limit을 해준다고 했으니 일단은 [0, 𝛕] 구간을 δ의 길이를 갖도록 쪼개주자.
  → Then, n = # of slots = 𝛕 / δ

• 그럼, 여기서 δ를 무한대로 보내버리면 continuous 상황을 만들 수 있을 것이다!

Key design idea to develop a Continuous Twin (2)

• 우리가 갖고 있는 아이디어는 : during one time slot of length δ
• 그럼 모델링을 위해 여기서 3가지의 상황을 생각해보자.
  1. 슬롯에 하나의 도착이 있을 확률
     → arrival rate와 slot length가 관련이 있을 것이다.
     → arrival rate가 높아지면 확률 상승, 반대면 반대 (slog length도 비슷)
  2. 슬롯에 두 개 이상의 도착이 있을 확률
     → 슬롯이 매우 작아지면 거의 없을 법한 확률이다.
  3. 슬롯에 도착이 없을 확률
     → 전체 확률(1)에서 [1]과 [2]의 확률을 빼주면 된다~!
• 수학적으로 이제 생각해보자.
  1. arrival rate와 slot length가 [1]의 확률에 영향을 끼치니
     → λδ
  2. 거의 없을 법한 확률이니까
     → 0
  3. 이건 [1]과 [2]를 빼면 되니까
     → 1 - λδ - 0
• 근데.. 없을 법한 확률이지 완전히 0은 아니다. 따라서 다음과 같이 수정을 해준다.
  1. λδ + o(δ)
  2. 0 + o(δ)
  3. 1 - λδ + o(δ)
• 여기서 o(δ)의 정의는 다음과 같다.
  → Some function that goes to zero faster than delta.
  → Thus, for very small delta, o(δ) becomes negligible, compared to δ.

Key design idea to develop a Continuous Twin (3)

• 지금까지 우리가 생각한 아이디어는 다음과 같다.

  • Given small δ,
    → # of arrivals : ~ Bin(n, p) where n = 𝛕 / δ and p = λδ

  • 그럼 여기서, δ → 0라고 한다면, np = 𝛕 / δ * λδ = λ𝛕
    → Oh! 어디서 봤던 것이다! 바로 Poisson rv!
    

    → [ δ → 0 ] == [ n → INF ]

  • 따라서, 다음이 성립되게 된다.
    
    

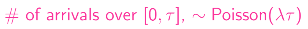
    → Expectation = λ𝛕 : mean # of arrivals * time