Algoritm Week 10

알고리즘 10주차 정리

최소 신장 트리 (최소 비용 트리, Minimum Spanning Trees)

• Tree
  • Cycle이 없는 연결 그래프
  • n 개의 정점을 가진 트리는 항상 n-1 개의 간선을 갖는다.
• 그래프 G의 신장 트리
  • G의 정점들과 간선들로만 구성된 트리
  • 한 그래프의 모든 노드들을 연결하기 위한 최소한의 간선들을 채택한 트리
  • 하나의 트리가 여러 개의 신장 트리를 가질 수 있음
• 그래프 G의 최소 신장 트리
  • G의 신장 트리들 중 간선의 합이 최소인 신장 트리

- 최소 신장 트리의 정의

• 무방향 가중치 그래프 G = (V, E)
• 각 Edge의 가중치 w(u, v)
• 문제 : 아래의 조건을 만족하는 Edge들의 부분 집합 T를 찾는 것
  1. T에 속한 Edge들에 의해 그래프의 모든 노드들이 서로 연결될 수 있다.
  2. 가중치의 합이 최소가 된다.
• 이를 만들 수 있는 알고리즘 두 가지
  1. 크루스칼 알고리즘 (Kruskal Algorithm)
  2. 프림 알고리즘 (Prim Alogorithm)

- Kruskal Algorithm

• 최소 신장 트리를 만들기 위한 알고리즘 중 하나
• Edge들을 가중치의 오름 차순으로 정렬
• 정렬된 Edge들을 순서대로 하나씩 선택
  • 단, 이미 선택된 Edge들과 Cycle을 형성하면 선택하지 않음
  • 동일한 값은 아무거나 선택해도 됨, (Cycle이 형성되지만 않는다면)
• n-1개의 Edge가 선택되면 종료
  → n개의 노드가 있는 트리는 항상 최소 n-1개의 간선을 갖는다.
  

- Pseudo Code

Kruskal(G, r)
1.  T ← Ф;	
2.	단 하나의 정점만으로 이루어진 n개의 집합을 초기화한다. → Connected Component
3.	간선 집합 Q(=E)를 가중치가 작은 순으로 정렬한다.
4.	while(T의 간선 수 < n-1)
5.		E에서 최소비용 간선 (u, v)를 제거한다
6.		정점 u와 정점 v가 서로 다른 집합에 속한다면
7.  		두 집합을 하나로 합친다.
8.  		T ← T∪{(u,v)}

1. T는 신장 트리를 의미
2. A, B, C, D 노드로 구성된 트리일 경우 A, B, C, D로 바꿈
   → 나중에, A와 B가 연결되면 (A, B), C, D가 됨
   → A와 B를 Connected Component라고 함
   

- Prim Algorithm

• 임의의 노드를 출발 노드{S}로 선택
• 매 단계에서 이미 트리에 포함된 노드와 포함되지 않은 노드를 연결하는 Edge들 중 가중치가 가장 작은 Edge를 선택하는 방식으로 Tree를 확장
  1. 모든 노드의 값을 무한대로 치환한다. 출발점은 0으로 한다.
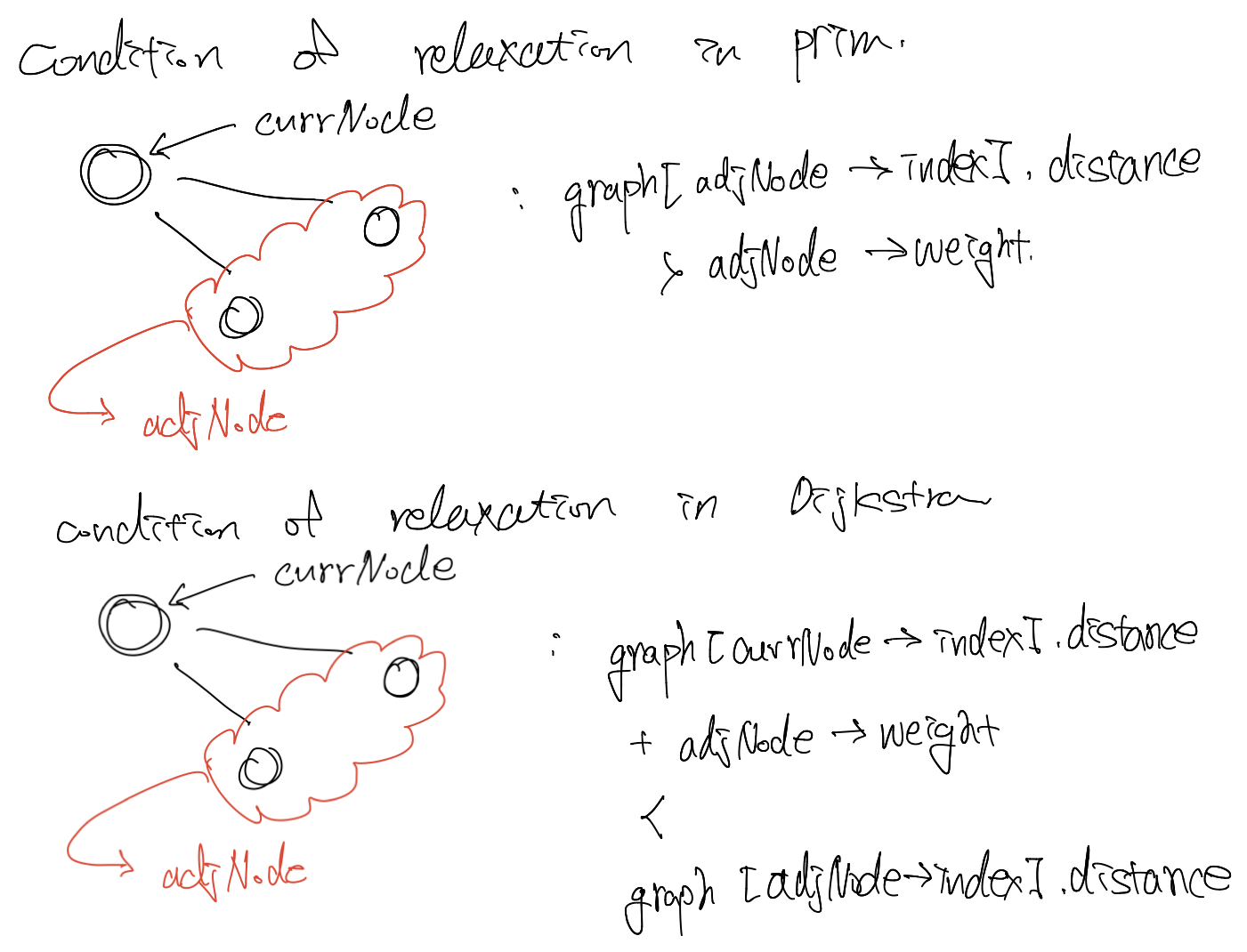
  2. 먼저, 현재 노드에서 연결된 노드에 대한 relaxation(이완) 진행
  3. S에 포함된 노드들에서 연결된 간선 중 최소 값 선택
  4. 그 간선에 연결된 노드를 S에 포함시킴
• 한 번 바뀐 S는 믿음이 된다. 추가만 해라.💩

- Pseudo Code

최단 경로 알고리즘

- Dijkstra Algorithm

• 조건
  • 간선 가중치가 있는 유향 그래프
  • 무향 그래프는 각 간선에 대해 양쪽으로 유향 간선이 있는 유향 그래프로 생각할 수 있다.
    → 즉, 무향 간선 (u, v)는 유향 간선 (u, v)와 (v, u)를 의미한다고 가정하면 된다.
• 두 정점 사이의 최단 경로
  • 두 정점 사이의 경로들 중 간선의 가중치 합이 최소인 경로
  • 간선 가중치의 합이 음인 Cycle이 존재한다면 문제가 정의되지 않는다.

- Pseudo Code

→ Prim Algorithm과 같다.
→ Relaxation 부분이 다르다!