Algoritm Week 14

Algorithm Week 14

Direct Addressing Table

• 두 개의 자료 구조 집합인 U와 T를 갖는 자료 구조
  → U : Universe of keys, key를 저장하고 있는 집합, 이 중 실제 사용되는 집합을 K(actual keys)라고 한다.
  → T : Table, | U |개의 slot으로 이루어져 있고, 각 slot은 Key와 Satellite data의 쌍으로 구성되어 있다.
  → key k → slot k
• T에서의 slot은 | U |개의 key를 포함할 수 있는 만큼의 메모리 구조를 미리 할당 받음
  → 따라서, 데이터 충돌은 일어날 수 없음.
  → 서로 다른 원소는 동일한 key를 갖지 않는다.
• 단순한 구조를 갖고 있기 떄문에, Search, Insert, Delete 연산에서 O(1)의 수행 시간을 갖는다.
  
• | U |개의 slot을 생성해야 하기 때문에, 메모리 공간 소비가 상당함
  → 실용적이지 않음, 컴퓨터 메모리의 한계
• 실제로 이용하고 있는 key들의 집합을 K라고 했을 때, | U |에 비해 | K |는 너무 작음
  → 수행 시간 O(1)을 유지하면서, 메모리 공간을 보다 효율적으로 이용할 방법을 찾게 됨
  
  

Hash Table

Hash Function

• 해시 함수 : 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수

  • 해시 함수에 의해 얻어지는 값 : 해시 값, 해시 코드, 해시 체크섬, 해시
  • 해시 테이블에 이용되는 함수 → 매우 빠른 데이터 검색 가능
  • 전송된 데이터의 무결성을 확인해주는 데 사용 → 블록체인
    

  
  

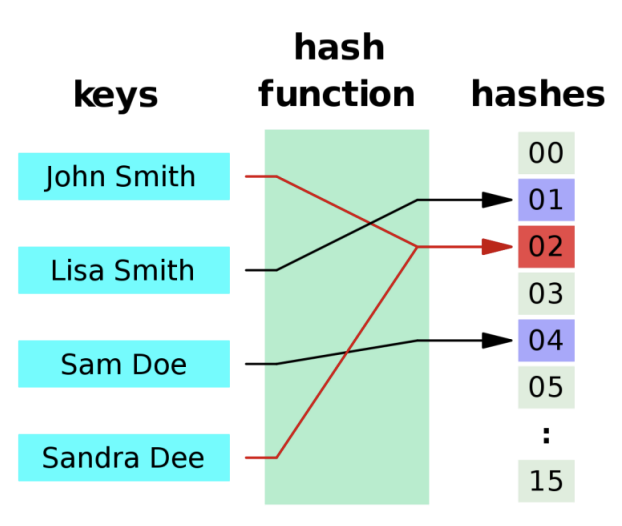
Hash Table

• 해시 함수를 사용하여 Key를 hash value로 매핑하며, 해당 값을 배열의 index로 이용하여 slot에 접근하는 자료구조
• 원소가 저장될 자리가 원소의 값에 의해 결정되는 자료 구조
  
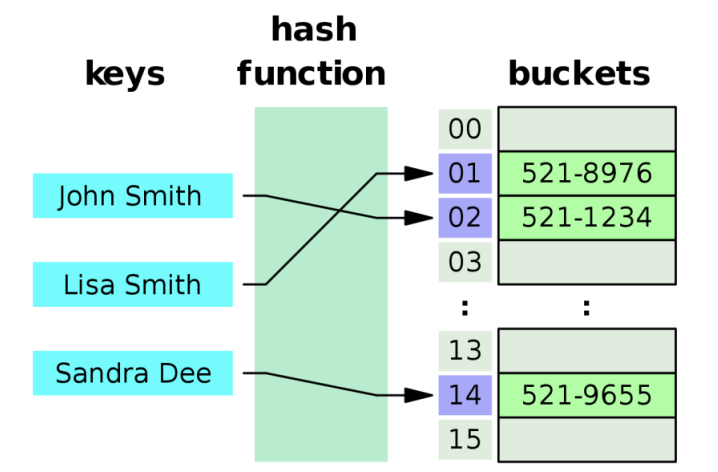
• Key k를 갖는 원소는 slot h(k)에 저장
  → h : hash function
• key k 가 h(k)로 “해싱 되었다”라고 표현
  
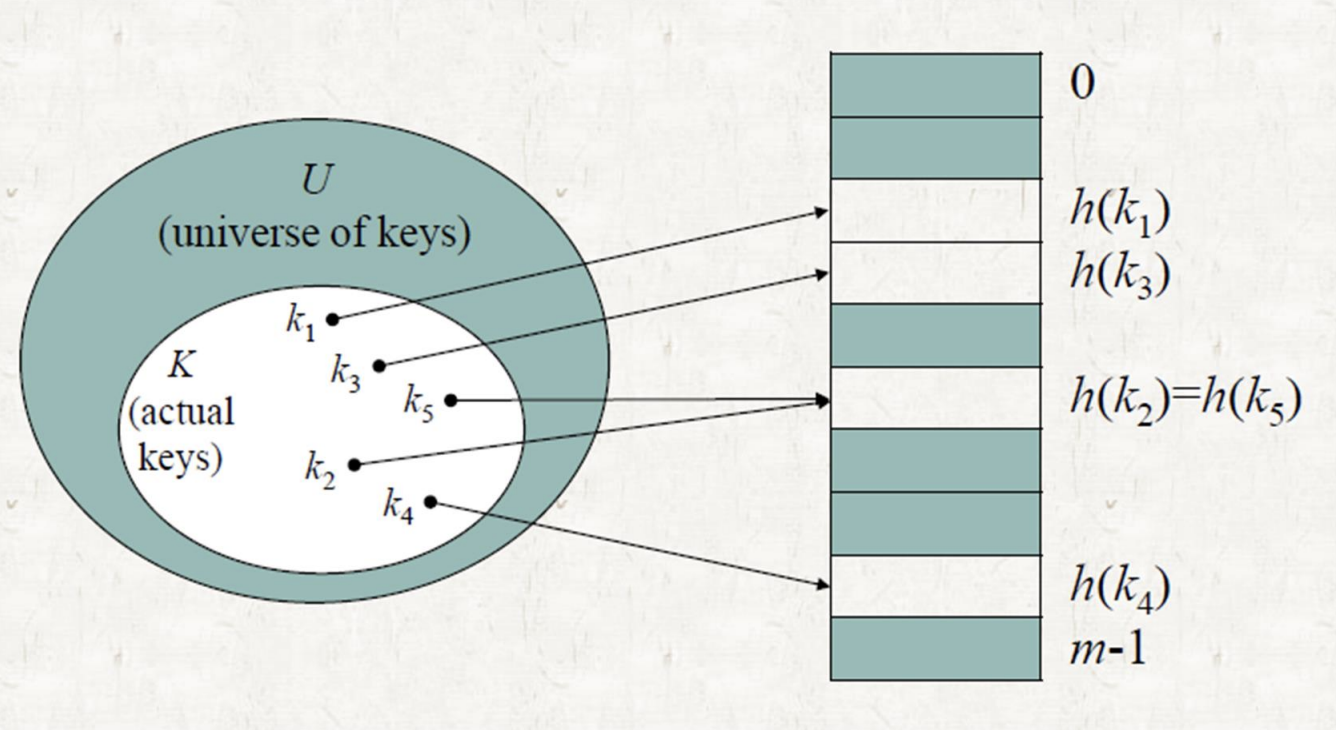
  → K에 있는 원소들은 Hash function(h)을 통과하여 인덱스(h(k))를 생성
  → 해당 인덱스를 사용하여 slot에 값을 저장
  → k2와 k5는 값이 동일한 곳에 저장되고, 이를 Collision이라고 부름
  

Collision

• 충돌 문제
  1. 서로 다른 두 키에 대해, h(k1) = h(k2)인 상황
  2. 두 개 이상의 키가 동일한 slot에 해싱되는 상황
• 해결 방법
  1. 좋은 해시 함수를 사용하여 충돌을 최소화
     → h를 random function처럼 작동하도록 설계
  2. 충돌 회피는 불가능
     → 전체 집합 자체의 크기가 너무 크고, 인덱싱하려는 slot의 크기가 상대적으로 작음
  3. 충돌 해결
     1. Chaining
     2. Open Addressing

Chaining

• 연결 리스트를 이용하여 동일한 해시 값을 갖는 원소를 관리
• Slot j는 j로 해싱된 모든 원소들을 지니고 있는 연결 리스트의 HEAD를 가리키게 함
  
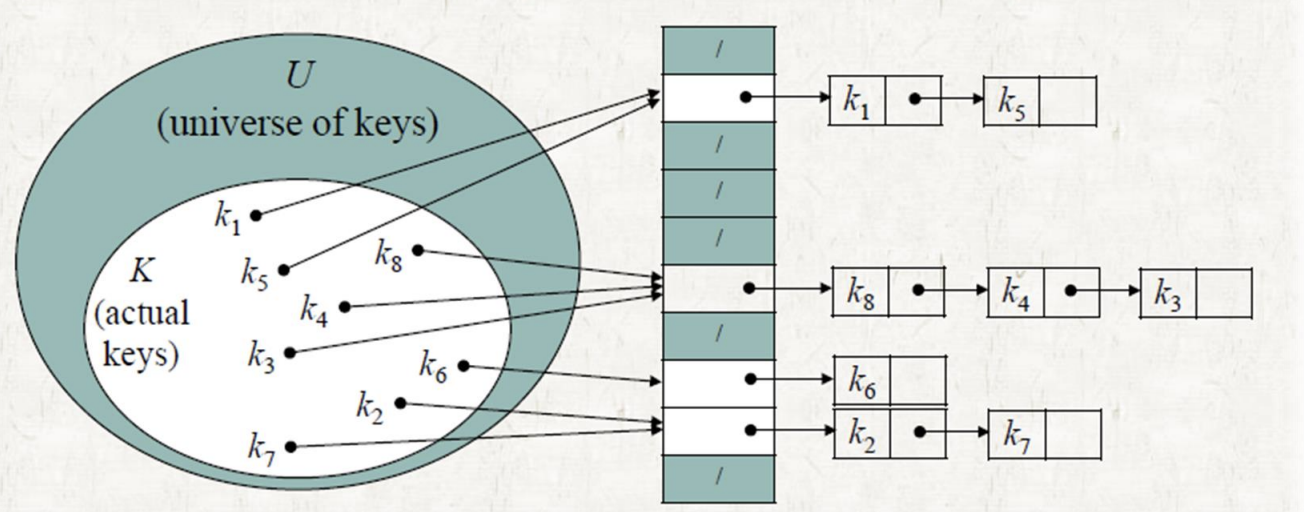
• Insert, Delete, Search
  
  1. Insert : O(1)
     → 삽입 시, 중복된 키가 들어올 경우 끝에 이어 붙여야 하기 때문에, O(n) (n은 리스트의 길이)
  2. Search : O(n)
     → 최악의 경우, 모든 Key가 동일한 slot에 해싱이 되었을 경우 → 저장 형태가 단순 연결 리스트
  3. Deletion : O(1)
• Load factor : Chaining의 성능을 평가하는 지표
  • 각 체인의 평균 길이
  • a = |U| / m
    → m : 테이블의 크기 (테이블에 저장된 원소의 수)
  • 알파 값이 작을 수록 좋은 경우

Open Addressing

• 개방 주소 방법
• 모든 원소는 해시 테이블 자체에 직접 저장
  • Chaining처럼, 테이블 밖에 원소를 저장하는 리스트가 필요하지 않음
  • 충돌이 일어나더라도 주어진 테이블 공간에서 해결
  • 즉, 해시 테이블의 각 slot에는 1개의 원소만 저장
• 대표적인 구현 방법
  1. 선형 조사 (Linear probing)
  2. 이차원 조사 (Quadratic probing)
  3. 더블 해싱 (Double hashing)
• Insertion
  • Empty slot을 찾을 때 까지, probing 후 Insertion 진행
    • 빈 자리가 생길 때까지 해시 값을 계속 만들어냄
    • 키의 저장 상태에 따라, 검색/조사하는 위치의 순서는 달라짐
• Search (동일)
• Deletion
  
  

• 선형 조사
  

  • 다음과 같은 mod 연산이 있는 함수를 사용해서 한다고 가정을 했을 때, 값이 연속해서 채워지는 형태가 됨
  • 그 중 중복이 생겼을 경우, i의 값을 증가시켜 다른 sequence를 구성하도록 함
  • Primary Clustering
    • Cluster : 앞서 말한 sequence가 이를 뜻하고, 키에 의해 채워진 연속된 slot의 집합
    • Cluster가 커질 수록 search time이 길어지고, 이는 당연히 길어질 수 밖에 없는 구조

• 이차원 조사
  

  • i에 2차항을 추가함으로써 건더뜀을 멀리 할 수 있도록 함
  • Secondary clustering
    • 두 개의 동일한 키 값이 있을 때, 같이 건너 뛰어다니는 속성이 있음

• 더블 해싱
  

  • 두 개의 해시 함수를 사용하여 해싱하는 방법

• Open Addressing의 문제점

  • 키를 삭제할 경우 문제가 발생할 수 있음
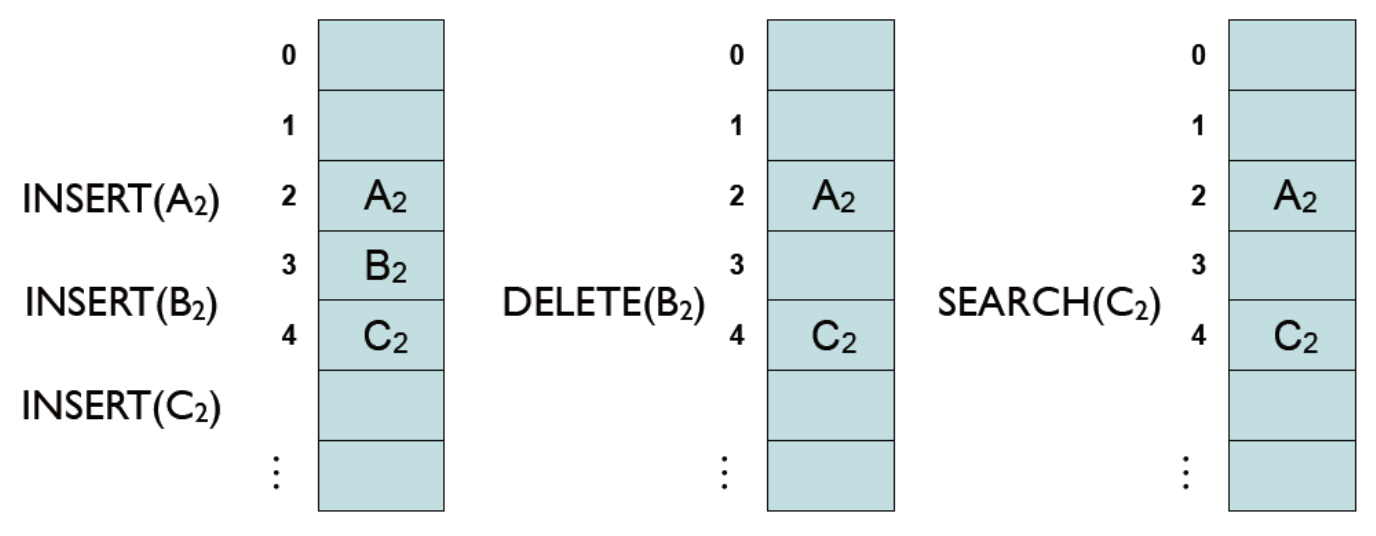
  • A2, B2, C2가 순서대로 모두 동일한 해시 값을 갖는다고 하면, 연산에는 문제가 없음
  • 이 중 B2를 삭제하고 나면, 이후 C2를 찾을 때 문제가 발생할 수 있음(원래는 연속이여야 하지만 삭제로 인해 아니기 때문)
    

  
  

  
  

  Hash functions

  • 모든 데이터는 수로 표현 가능
  • 문자열의 경우, 어떤 방식으로 수로 바꾼 뒤, Division Method로 변경하는 등의 방식이 있음
  • 해시 함수의 평가
    • 해시 함수가 저장될 키 값들을 m개의 슬롯에 얼마나 잘 분배하는지를 척도로 평가
  • 좋은 해시 함수
    • 해시 함수는 deterministic. 따라서, 현실에서는 키들이 랜덤하지 않음
    • 키들의 통계적 분포에 대해 알고 있다면, 이를 이용해서 해시 함수를 고안하는 것이 가능
      → 사실상 불가능한 방법
    • Simple Uniform Hashing Assumption(SUHA)을 만족하는 함수
      • 각 키가 모든 slot들에 균등한 확률로 해싱
      • 각 키는 독립적으로 해싱
    • 키들이 규칙을 가지고 있더라도, 해시 값이 불규칙적으로 나오는게 바람직
    • 해시 값이 키의 특정 부분에 의해 결정되면 안됨