Algoritm Week 2

알고리즘 2주차 강의 정리

• 알고리즘이란?

  • 문제를 해결하는 단계적 절차 또는 방법을 의미 → 단, 컴퓨터를 이용하여 해결할 수 있어야 함
  • 알고리즘에는 입력이 주어지고, 알고리즘은 수행한 결과인 해를 출력해야 함 → 알고리즘 = 함수 혹은 모듈, 크게는 프로그램

• 알고리즘의 특성

  1. 정확성 : 주어진 입력에 대해 올바른 해를 구한다. → 예외 사항에 대한 처리가 올바른가?
  2. 수행성 : 알고리즘의 각 단계는 컴퓨터에서 수행이 가능해야 한다.
  3. 유한성 : 알고리즘은 일정 시간 내에 종료되어야 한다.
  4. 효율성 : 알고리즘은 효율적일수록 그 가치가 높아진다. → 시간 복잡도, 공간 복잡도 → 이 둘은 trade-off 관계에 있음

• 알고리즘의 표현 방법

  • 흐름도(flow chart), 의사 코드(pseudo code) → 의사 코드 : 프로그래밍 언어로 된 진짜 코드와 유사한 표현, 문법적 오류를 크게 신경쓰지 않음 → 언어 종속성이 없는 표현 방식으로, 오해의 소지가 없음

• 알고리즘 분석의 필요성

  • 효율성 : 알고리즘의 수행 시간 또는 수행되는 동안 사용되는 메모리 공간의 크기
    • Time complexity : 일반적으로 효율성 측정을 위해 사용됨 (유한성과 관련됨)
    • Space complexity
  • 시간 복잡도, 즉 실행 시간은 실행 환경에 따라 달라지게 됨 → 하드웨어, 운영체제, 언어, 컴파일러 등
  • 실행 시간을 측정하는 대신, 알고리즘이 실행되는 동안에 사용된 단위 연산 횟수를 측정 → For-loop의 반복 횟수, 특정한 행이 수행되는 횟수, 함수 호출 횟수 등… → 이러한 연산의 실행 횟수는 입력 데이터 크기에 관한 함수로 표현 → 데이터의 크기가 같더라도 실제 데이터에 따라 달라질 수 있음 (최악의 시간 복잡도) → 정렬 알고리즘에서 {1,2,3,4,5}와 {1,2,4,3,5}는 데이터의 크기가 같지만 시간 복잡도는 다름

• 알고리즘의 수행 시간 == 단위 연산의 횟수

  sample1(A[], n){
  	k = [n/2];
  	return A[k]
  }
  

  → n에 관계없이, 그리고 A 배열의 값에 관계 없이 일정한 시간이 소요 → O(1)

  sample2(A[], n){
  	sum = 0;
  	for i = 1 to n
    	sum = sum + A[i];
    return sum;
  }
  

  → n에 비례하는 시간이 소요 됨 → O(n) : 선형 시간 복잡도를 갖는다.

  sample3(A[], n){
  	sum = 0;
  	for i = 1 to n										# n번의 반복
  		for j = 1 to n									# n번의 반복
  			sum = sum + A[i] * A[j];
  	return sum;
  }
  

  → n^2 에 비례하는 시간이 소요 → O(n^2)

  sample4(A[], n){
  	sum = 0;
  	for i = 1 to n										# n번의 반복
  		for j = 1 to n									# n번의 반복
        k = A[1...n]에서 임의의 값을 [n/2]개 뽑을 때, 이들의 최댓값; # n/2 - 1 반복
  			sum = sum + k;
  	return sum;
  }
  

  → O(n * n * (n/2 -1)) = O(n^3)

  sample4(n){
  	if (n = 1) return 1;				# 종료 조건
  	return n*sample4(n-1);			# recursive
  }
  

  → n에 비례하는 시간 소요 (O(n))

  • 효율적 알고리즘의 필요성

    O(n^2)	1000개	1백만개	10억개
    PC	< 1s	2 h	300 y
    슈퍼컴	< 1s	1 s	1 week

    O(nlogn)	1000개	1백만개	10억개
    PC	< 1 s	< 1 s	5 m
    슈퍼컴	< 1 s	< 1 s	< 1 s

    • SW 적으로 효율적인 알고리즘 개발이 HW 보다 경제적이다~!

• 점근적 분석

  • 입력의 크기가 작은 경우, 효율성이 중요하지 않고 비효율적인 알고리즘이더라도 허용됨

  • 입력의 크기가 커질 경우, 효율성이 매우 중요하고 비효율적인 알고리즘은 치명적

  • 같은 문제를 해결하는 알고리즘들의 수행 시간이 수백만 배 이상 차이가 날 수 있다.

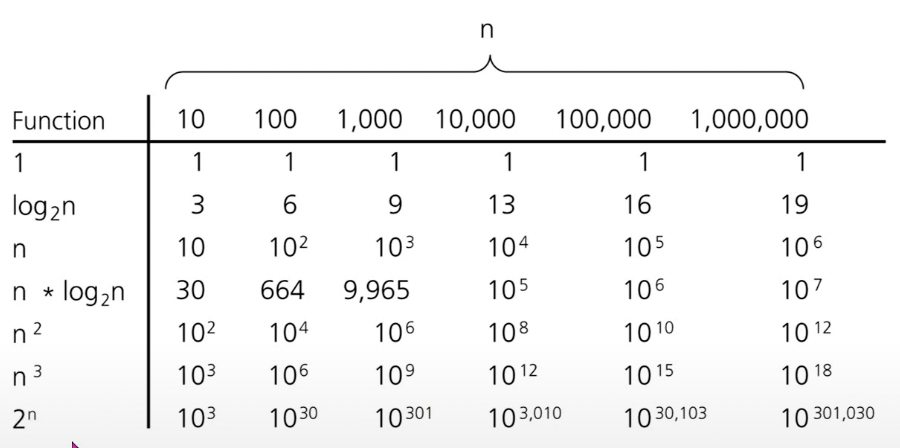
  • 입력의 크기가 커질 때, 알고리즘의 효율성을 판단하는 도구가 ‘점근적 분석’

  • 점근적 표기법 : 점근적 분석을 위해 사용되는 표현법 → 입력의 크기가 무한히 커질 때, 수행 시간이 증가하는 growth rate로 시간 복잡도를 표현하는 기법 (고등학교 수학에서 배운 lim의 개념과 같음) → Big-Oh notation, Omega Notation, Theta Notation → 알고리즘을 분석할 때는 평균적, 최고 성능이 아닌 “최악의 성능”을 따져야 함 (최고차 항의 차수, dominant한 항을 봄) == 가장 자주 실행되는 연산, 혹은 문장만 고려해도 된다는 의미

    • Big-Oh Notation

      • 모든 n(상당히 큰, >= n0)에 대해서 f(n) <= cg(n) 이 성립하는 양의 상수 c와 n0가 존재하면, f(n) ∈ O(g(n))이다. → f(n)은 내가 만든 코드의 시간 복잡도를 의미 → g(n)은 어떠한 시간 복잡도를 의미하고 상한(Upper bound)이라고 함 예시) f(n) = 32n^2 + 17n - 32 < 33n^2 (n > n0, n0는 33n^2이 더 커지는 순간) → f(n) ∈ O(n^2) 이라고 표시할 수 있음 → 물론, f(n) < cn^3 이기 때문에 f(n) ∈ O(n^3)라고 할 수 있지만, 최대한 tight하게 작성하는 것이 원칙

    • Big-Omega Notation

      • 모든 n(상당히 큰, >= n0)에 대해서 f(n) >= cg(n) 이 성립하는 양의 상수 c와 n0가 존재하면, f(n) ∈ Ω(g(n))이다.
      • g(n)을 f(n)의 하한(Low bound)이라고 한다.

    • Theta Notation

      • 모든 n(상당히 큰, >= n0) 대해서 c1g(n) >= f(n) >= c2g(n)이 성립하는 양의 상수 c1, c2, n0가 존재하면, f(n) ∈ Θ(g(n)) 이다.
      • 수행 시간을 표기할 때, Big-Oh와 Big-Omega가 동일한 경우를 의미한다.
      • f와 g가 동일한 차수를 가지며, 증가율이 동일하다는 의미를 갖는다.

    • Some commonsense Rules

      1. Multiplicative constants can be omitted
      2. n^a dominates n^b if a > b
      3. Any exponential dominates any polynomial
      4. Any polynomial dominates any logarithm