Algoritm Week 4

알고리즘 4주차 정리

Recursion

• 순환, 재귀 함수(Recursive Function)

• 함수를 재호출하는 함수로
  → 직접 재귀 함수 : 자기 자신을 호출하는 함수
  → 간접 재귀 함수 : A가 B를 부르고, B가 A를 다시 부르는 함수
  

  void function_(...)
  {
  	...
  	function_(...);
  	...
  }
  

• 연속된 자연수의 합을 재귀함수로 구현한 예시

  int sum(int n){
    if(n==1)							// Base case
      return 1;
    else									// Recursive case
      return n+sum(n-1);
  }
  

  → 재귀함수는 ‘Base case(종료 조건)’이 필수적으로 필요함
  

• 또한, 재귀함수는 stack 자료 구조 형태로 생각할 수 있음

• Factorial

  int factorial(int n){
    if (n == 0)
      return 1;
    else 
      return n * factorial(n-1);
  }
  

• Fibonacci

  int fibonacci(int n){
    if(n==0)
      return 0;
    else if (n == 1)
      return 1;
    else
      return fibonacci(n-1) + fibonacci(n-2);
  }
  

  
  

Divide-and-Conquer

• 분할 정복
• 한 문제를 유형이 비슷한 여러 개의 하위 문제로 나누어 재귀적으로 해결하고 이를 합쳐 원래 문제를 해결하는 방법
• 분할 정복의 작동 순서
  1. 분할 : 문제를 비슷한 유형으로 나눔
  2. 정복 : 나눠진 부분에서 ‘부분 해’를 구함
  3. 병합 : 구해진 부분 해를 합쳐 ‘최종 해’를 구함
• 하위 문제 각각은 원래 문제보다 범위가 작아야 하며, 하위 문제는 각 문제마다 탈출 조건이 반드시 존재해야 함
  

Merge Sort - Advanced Sort

• 폰 노이만이 1945년에 개발한 분할 정복 알고리즘
  → 모든 원소를 다 나눈 다음에 병합하는 방식으로 정렬을 수행💩

• 효율적인 알고리즘으로서, 시간 복잡도 O(nlogn)을 갖는다.

• 분할 정복의 원리 in Merge Sort

  1. 분할 : 원소가 1개 남을 때 까지
  2. 정복 : 재귀적으로 합병 정렬을 이용해 정렬
  3. 병합 : 다시 n개가 될 때 까지
     

• 그림으로 이해해보자.
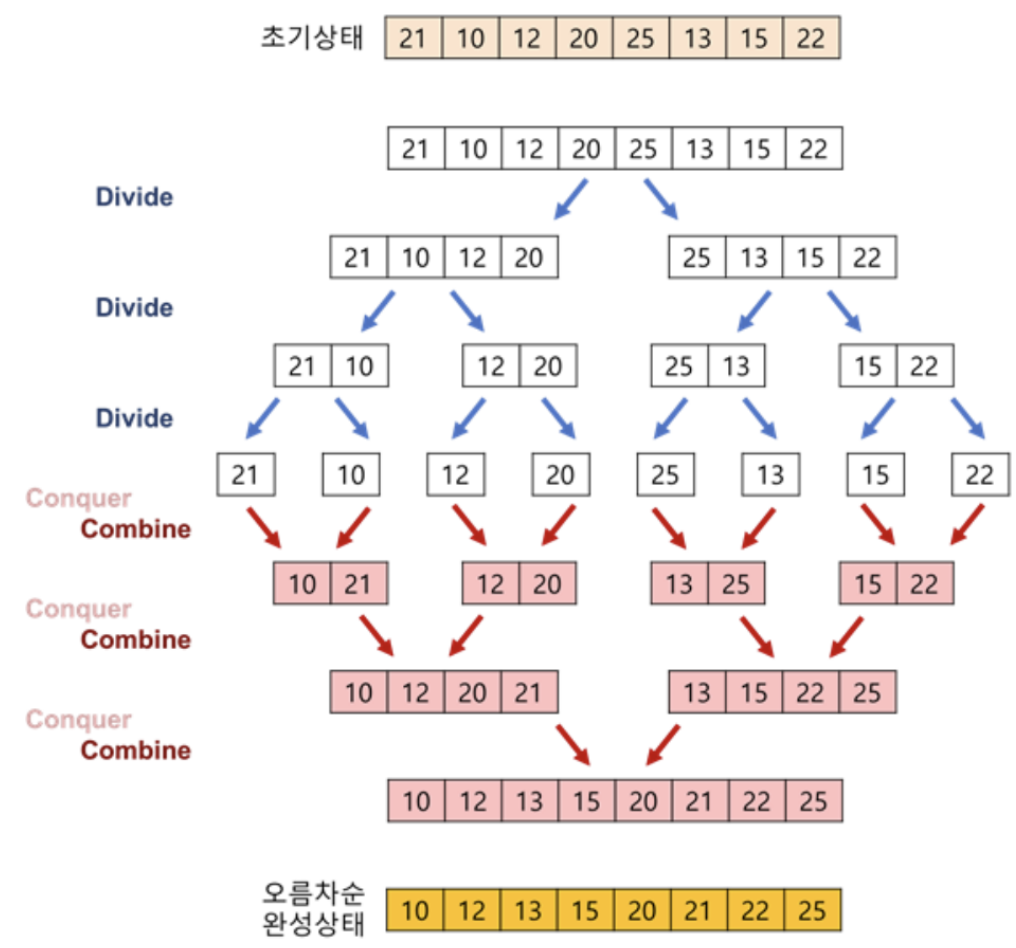
  → 그림에도 나와있 듯이, 각각의 정렬 정보를 저장할 ‘임시 배열‘이 필요함
  

• Pseudo Code

  mergeSort(A[], p, r)			// A[p...r]을 정렬
  {
  	if (p<r) then {
      q ← floor((p+r)/2);		// p, q의 중간 지점 계산
      mergeSort(A, p, q);		// 전반부 정렬
      mergeSort(A, q+1, r);	// 후반부 정렬
      merge(A, p, q, r);		// 병합
    }
  }
    
  merge(A[], p, q, r){
    정렬되어 있는 두 배열 A[p...q]와 A[q+1...r]을 합쳐
    정렬된 하나의 배열 A[p...r]을 만든다.
  }
    
  

  
  

• C code - merge

  void merge(int* A, int p, int q, int r){
    int i=p, j=q+1, k=p;
      
    while(i<=q && j<=r){					// 비교하며 삽입
      if (A[i] > A[j]){
        temp[k++] = A[j++];
      }
      else{
        temp[k++] = A[i++];
      }
    }
      
    while(i<=q)										// 남은 애들 쑤셔 넣기
      temp[k++] A[i++];
    while(j<=r)
      temp[k++] A[j++];
      
    for(i = p; i<=r; i++){
      A[i] = temp[i];
    }
      
    return ;
  }
  

  • temp 선언이 없는 것을 통해 temp는 global 변수임을 알 수 있다.
    → why? : 함수를 돌면서 매번 temp 함수를 선언하고 반환하는 작업에서 딜레이가 발생할 수 있기 때문.
    

• 정리

  1. 분할 과정과 정복 과정으로 나누어짐
  2. 모든 원소를 독립적으로 재귀적 균등 분할 후, 병합 시 정렬
  3. 시간 복잡도 : O(nlogn), worst case와 best case에서도 동일
     

Quick Sort - Advanced Sort

• 평균적으로 매우 빠른 수행 속도를 보장하는 알고리즘 ( O(nlogn) )

• 분할 정복 알고리즘 (비균등 분할)

• 피벗을 정한 뒤, 피벗의 위치를 확정해가며 정렬을 수행
  → 피벗보다 큰 값은 앞으로, 작은 값은 뒤로 (물론, 기준에 따라)

• 분할 정복의 작동 순서

  1. 분할 : 피벗을 기준으로
  2. 정복 : 재귀적으로, 분할된 부분의 크기가 0이나 1이 될 때까지
  3. 병합 : 진행하지 않는다.
     

• 그림으로 작동 원리를 간단히 파악해보자.💩
  

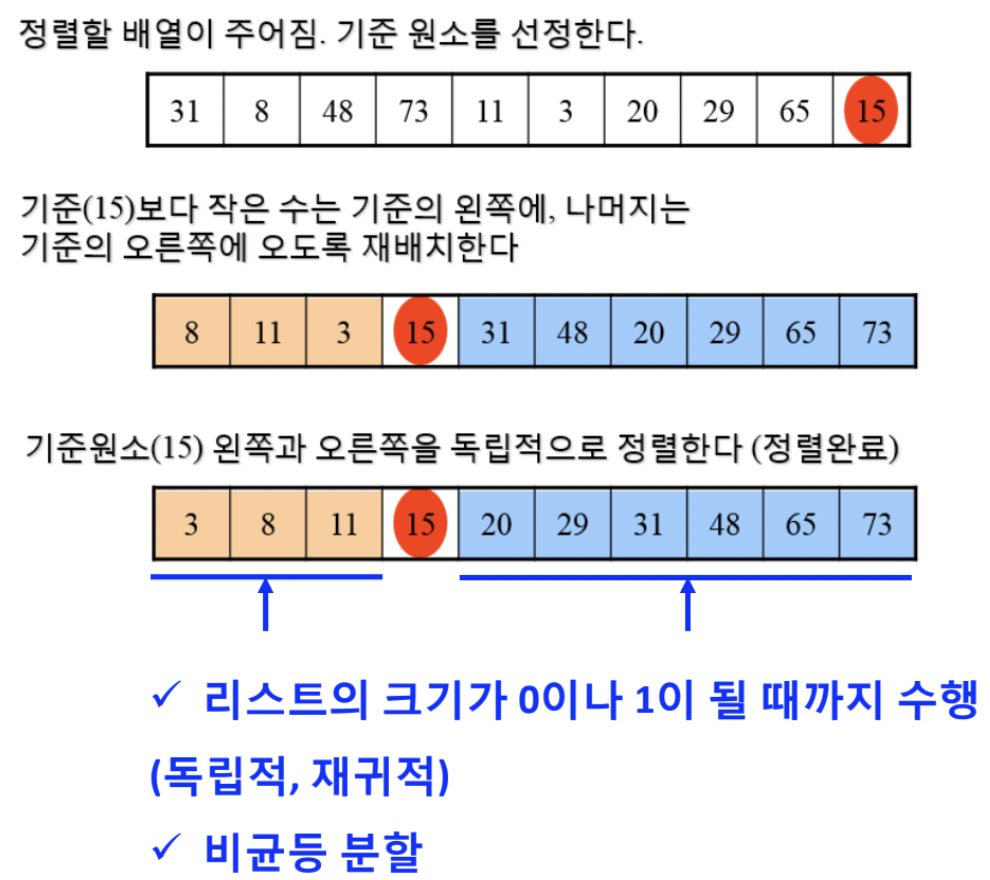
• Pseudo Code

  quickSort(A[], p, r)
  {
    if (p<r) then {
      q = partition(A, p, r);	// 분할
      quickSort(A, p, q-1);		// 피벗의 왼쪽 부분 정렬
      quickSort(A, q+1, r);		// 피벗의 오른쪽 부분 정렬
    }
  }
    
  partition(A[], p, r){
    // 배열 A[p...r]의 원소들을 A[r]을 기준으로 양쪽으로 재배치하고
    // A[r]이 자리한 위치를 리턴한다.
    x ← A[r];								// pivot
    i ← p-1;
    for j ← p to r-1
      if A[j] <= x then
        i ← i+1;
    		swap(A[i], A[j]);
    swap(A[i+1], A[r]);
    return i+1;
  }
  

  
  

• partition 함수의 동작 원리는 다음 그림과 같다.
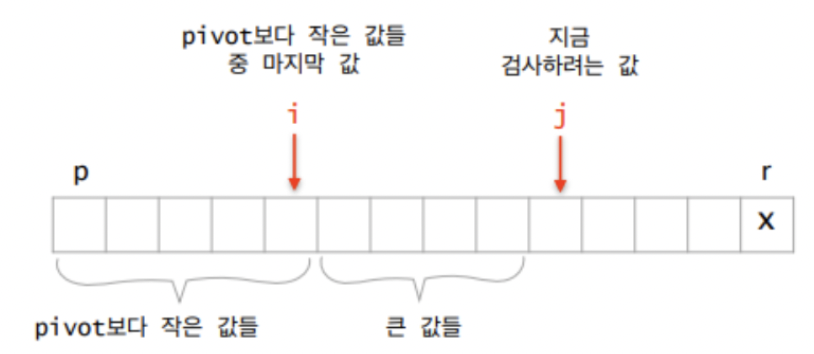
  → 피벗이 정렬된 후, 위치할 곳을 return 한다는 것을 명심하자.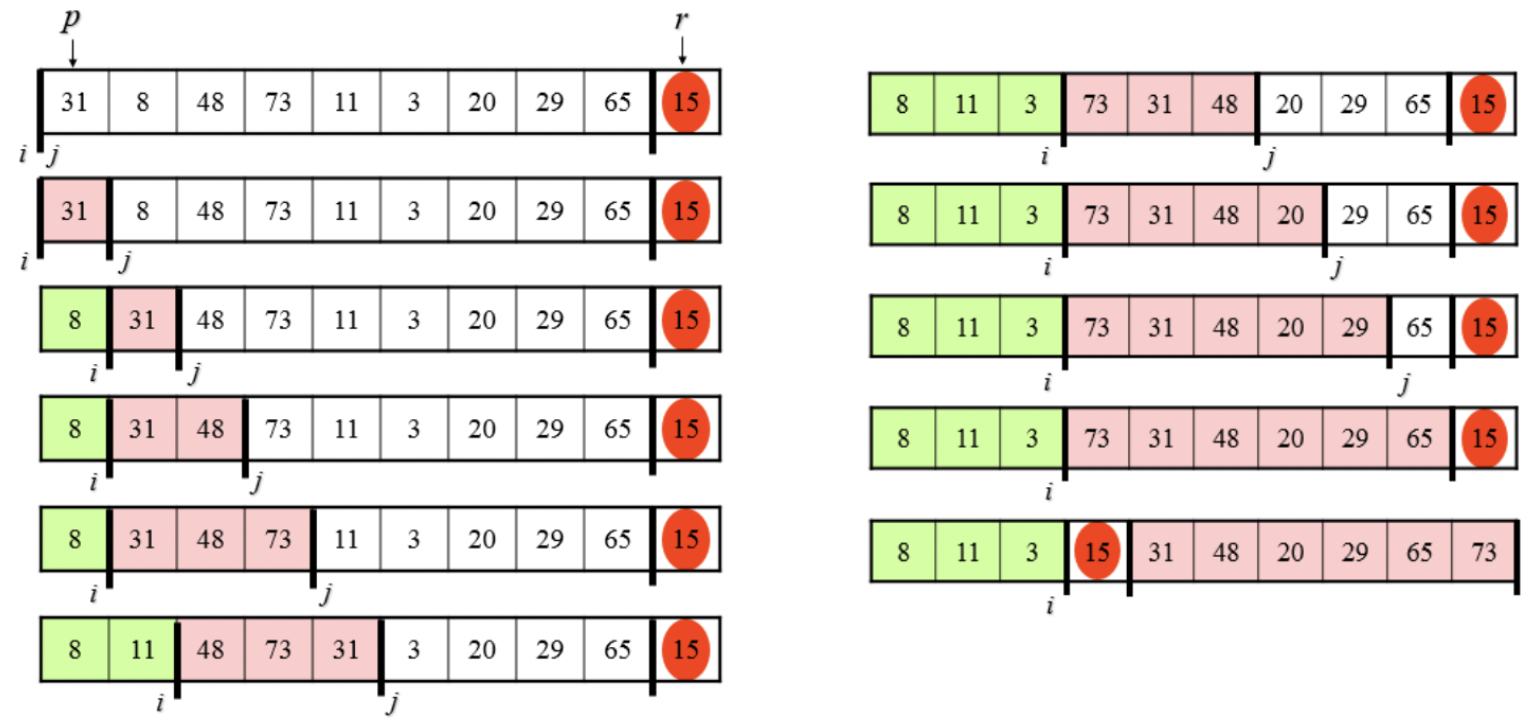
  

• 정리

  1. 분할 과정과 정복 과정으로 나누어져 진행
  2. 피벗을 정한 뒤, 왼쪽/오른쪽 독립적으로 Quick Sort를 재귀적으로 수행
  3. 피벗 선정 방식에 따라 다양한 Quick Sort
     → Randomized Quick Sort
  4. 시간 복잡도 O(nlogn)
     → Worst Case : O(n^2)
     → 이미 정렬된 배열에서 발생
     

  최종 정리~!

  Sorting Algorithm	Worst Case	Average Case
  Selection Sort	n^2	n^2
  Bubble Sort	n^2	n^2
  Insertion Sort	n^2	n^2
  Merge Sort	nlogn	nlogn
  Quick Sort	n^2	Nlogn