Algoritm Week 6

알고리즘 6주차 정리

Binary Tree Traversal

• Binary Tree Representation

  • 쉽게 부모, 왼쪽 자식, 오른쪽 자식의 위치를 쉽게 결정할 수 있음
  • 심지어, complete binary tree에서는 어떤 노드가 i라는 번호를 가질 때, (각 노드에 1~n까지 번호를 부여)
    1. parent(i) = floor(i/2)
    2. leftChild(i) = 2i
    3. rightChild(i) = 2i + 1

• Linked structure representation

  • 자료구조 중 하나인 Linked List를 사용하여 표현할 수 있다.
    

    
    

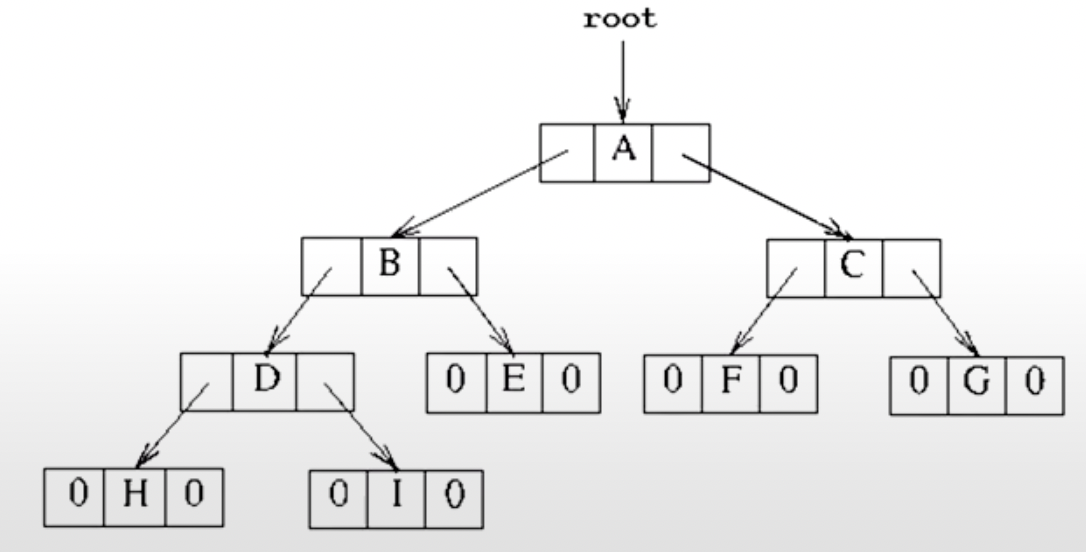
• 순회(Travesal)

  • 이진 트리의 모든 노드를 방문하는 일
    

    
    

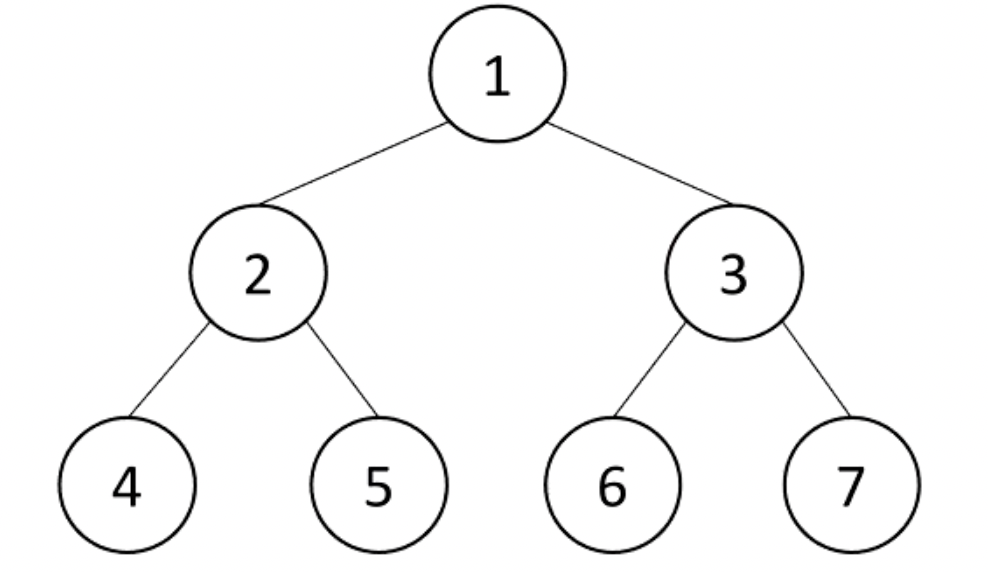
  • Pre-order (선) : Root-Left-Right
    → 1 2 4 5 3 6 7

  • In-order (중) : Left-Root-Right
    → 4 2 5 1 6 3 7
    → 이진 트리의 연결 관계가 루트(왼쪽보다 크고 오른쪽보다 작음), 왼쪽 자식(루트보다 작고 오른쪽 자식보다 작음), 오른쪽 자식(루트보다 크고, 왼쪽 자식보다 큼)일 때, 오름 차순으로 정렬 가능

  • Post-order (후) : Left-Right-Root
    → 4 5 2 6 7 3 1

  • Level-order : 단순히 트리의 레벨에 따라 레벨에 존재하는 값을 읽는 것
    

    LEVEL-ORDER-TREE-TRAVERSAL()
      visit the root;
    	Q ← root;		// Q is a queue
    	while Q is not empty do
        v ← dequeue(Q);
    		visit children of v;
    		enqueue children of v into Q;
    	end;
    end;
    

    → 1 2 3 4 5 6 7