Algoritm Week 7

알고리즘 7주차 정리

Binary Search Tree

• Dynamic Set

  • Search, Insert, Delete 등의 기능을 제공하는 자료구조
  • 배열, 연결리스트, Hash Table 등 선형 구조 이용
    → Insert, Search, Delete 중 적어도 하나는 O(n)
  • 이진 탐색 트리 : 레드-블랙 트리, AVL-트리 등의 트리 기반 구조 이용 → Insert, Search, Delete 연산의 시간 복잡도 O(h), h = log n
    

• 이진 검색 트리

  • 검색 트리 중 하나 - 자료의 검색을 빠르게 하기 위함
  • 이진 트리의 구조 → 완전 이진 트리는 아님!
  • 각 노드에 하나의 KEY를 저장
  • 임의의 노드 v에 대하여, 왼쪽 서브트리에 있는 KEY들은 KEY[v]보다 작거나 같다.
    → KEY[x] <= KEY[v]
  • 임의의 노드 v에 대하여, 오른쪽 서브트리에 있는 KEY들은 KEY[v]보다 크거나 같다.
    → KEY[x] >= KEY[v]
  • 서브 트리 또한 이진 검색 트리
  • 중순위 순회를 한다면 이진 검색 트리에 있는 모든 값들을 오름차순으로 출력할 수 있음
    → Left - Root - Rigth
    → 순회 결과가 오름차순이 아니라면 이진 검색 트리 구조가 아님
    

Querying a Binary Search Tree

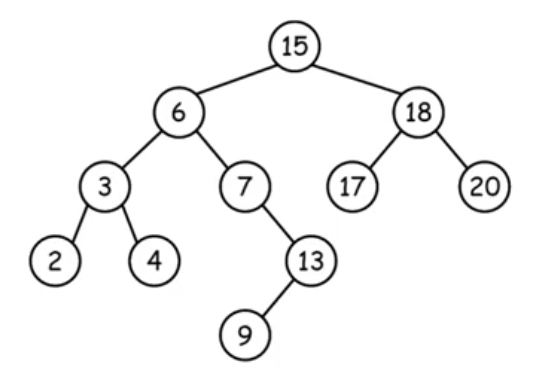
• SEARCH(13) : 15 → 6 →7 → 13
• MINIMUM : 2 → following left pointers from the root
• MAXIMUM : 20 → following right pointers from the root
• SUCCESSOR(15) : 17 (minimim key in the right subtree)
• SUCCESSOR(13) : 15 (lowest ancestor whose left child is also an ancestor)
  → 오른 쪽 부트리가 없을 때, 조상을 타고 쭉 올라가다가 처음으로 오른쪽으로 갈 수 있는 길이 나올 때

1. SEARCH

   TREE-SEARCH(x, k)
     if x == NULL or k = key[x]
       then return x
     if k < key[x]
       then return TREE-SEARCH(left[x], k)
     else TREE-SERACH(right[x], k)
          
          
   ITERATIVE-TREE-SEARCH(x, k)
       while x != NULL or k != key[x]
         do if k < key[x]
           then x ← left[x]
           else x ← right[x]
       return x
   

2. Minimum And Maximum

   TREE-MINIMUM(x)
     while left[x] != null
       do x ← left[x]
     return x
            
   TREE-MAXIMUM(x)
     while right[x] != null
       do x ← right[x]
     return x
   

3. Successor

   • Successor y of a node x : key[x]보다 크면서 가장 작은 key를 가진 노드
     → Inorder tree walk를 통해 찾는 방법
     → 이진 검색 트리의 구조를 통해 찾는 방법
   • 이진 검색 트리의 구조를 통해 찾는 방법
     • 노드 x의 오른쪽 subtree가 존재할 경우, 오른쪽 subtree의 최소값
     • 오른쪽 subtree가 없을 경우, the lowest ancestor of x, whose left child is also an ancestor of x

   TREE-SUCCESSOR(x)
     if right != NULL
       then return TREE-MINIMUM(right[x])
     y ← parent[x]
     while y != NULL and x == right[y]
       do x ← y
          y ← parent[y]
     return y
   

   • 오른 쪽 subtree가 없을 때, y에 현재 노드의 부모(조상)을 부여하고, x와 y가 자식-부모 관계를 갖도록 함
   • 이 때, x가 오른쪽 자식이 될 때, while을 끝냄
   • y가 NULL이 되면, X의 successor는 없음을 나타냄 → 즉, x는 MAXIMUM.
     

Insertion & Deletion

• Tree INSERT

  TREE-INSERT(T, z)  // T에 z 노드 삽입
    y ← NULL
    x ← root[T]
    while x != NULL  // y에 최종적으로 z의 부모가 되어야할 노드를 알려줌
      do y ← x
        if key[z] < key[x]
          then x ← left[x]
        else x ← right[x]
    parent[z] ← y
    if y = NULL
      then root[T] ← z			// Tree T was empty
    else if key[z] < key[y]
      then left[y] ← z
    else right[y] ← z
  

  
  

• DELETION

  • 노드 z의 자식 노드가 없는 경우
    → 삭제 / 부모 노드의 자식 노드를 NIL로 수정
  • 노드 z의 자식 노드가 1개인 경우
    → 삭제 / 노드 z의 부모와 자식 노드 링크 연결
  • 노드 z의 자식 노드가 2개인 경우
    1. 노드 z의 오른쪽 subtree에서 minimum을 찾음 → 노드 z의 successor
       → **항상 오른쪽엔 subtree가 존재하게 됨 **
       → 그로 인해, successor는 최대 1개의 자식 노드를 가짐
    2. successor를 잠깐 빼놓고, successor의 자식과 부모의 링크를 연결 (자식이 1개인 경우와 같이)
    3. 빼놓은 successor와 z를 바꾸고, z를 삭제

  TREE-DELETE(T, z)
  	if left[z] == NIL or right[z] == NIL  // 자식이 1개거나 없음
    	then y ← z      // y는 삭제할 노드를 명시
    else y ← TREE-SUCCESSOR(z)
        
    if left[y] != NIL
      then x ← left[y]
    else x ← right[y]
        
    if x != NIL  // 자식 노드가 1개 이상일 경우
      then parent[x] ← parent[y]
      
    if parent[y] == NIL
      then root[T] ← x    // Empty tree일 경우 
    else if y == left[p[y]]
      then left[p[y]] ← x
    else right[p[y]] ← x
        
    if y != z  // 자식 노드가 2개일 경우
      then key[z] ← key[y]
      		copy y's staellite data into z
    return y