Algoritm Week 9

알고리즘 9주차 정리

그래프 개념

- 그래프

• 현상이나 사물을 정점과 간선으로 표현한 것
• G = (V, E)로 표현한다.
  • V : 정점의 집합, vertex
    → 노드, 독립형 객체, circle로 표현
  • E : 간선의 집합, edge
    → 링크, 두 개의 정점을 연결하는 객체, 화살표 혹은 실선으로 표현
• 두 정점이 간선으로 연결되어 있으면 ‘인접한다(Adjacent)’라고 한다.
  
  

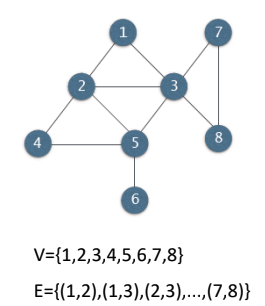
- 방향 그래프

• 방향이 있는 간선을 지닌 그래프, directed edges
• 각 간선은 하나의 정점을 떠나서, 하나의 정점으로 들어감
  → 자기 자신에게 들어갈 수도 있음(self-loop, self-edge)
• 두 정점 사이에 최대 2개의 간선 존재 가능
  
  

- 무방향 그래프

• 방향 간선이 없는 그래프, undirected graph(edges)
• Self-loop가 불가능

• (u, v) = (v, u)
  
  

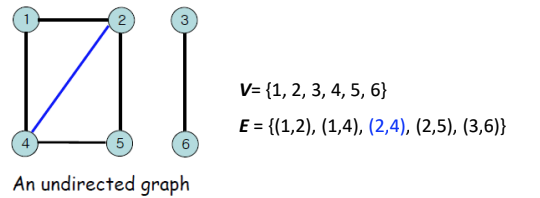
• 이 외에도, 가중치를 가진 무방향, 가중치를 가진 방향 그래프 등이 존재함

그래프의 표현

1. 인접 행렬 (Adjacency Matrix)

• n*n 행렬로 표현, n은 정점의 총 개수
  • M(i, j) = 1 → 정점 i와 정점 j 사이에 간선이 있음
  • M(i, j) = 0 → 정점 i와 정점 j 사이에 간선이 없음
• 방향 그래프의 경우
  • 원소 (i, j)는 정점 i로부터 j로 연결되는 간선이 있는지를 나타냄
  • 그래프가 저장된 Matrix의 대칭성이 깨지게 됨
• 가중치의 경우
  • 1 대신에 가중치 값을 삽입
    

2. 인접 리스트

• n개의 연결 리스트를 생성해서 표현
• i번째 리스트는 정점 i에 인접한 정점들을 리스트로 연결해서 사용
• 총 2*|E|개의 노드가 사용되게 됨
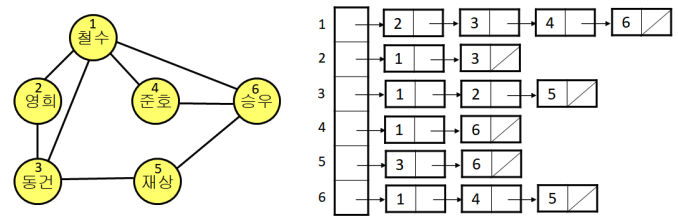
  → 새로운 값 삽입 시, 보통은 맨 앞에 새로 삽입함

그래프의 순회 - BFS, DFS

- BFS와 DFS 맛보기

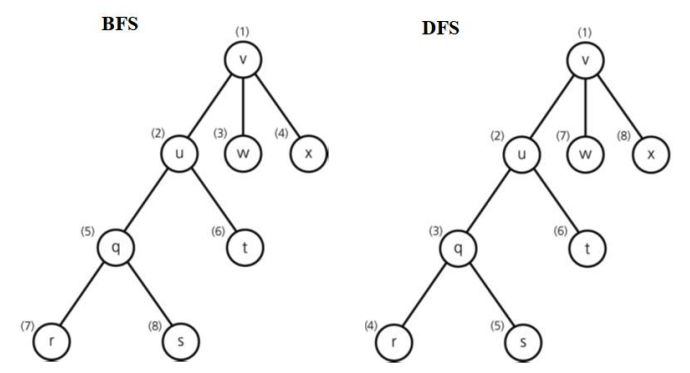
• (괄호 안에 숫자)가 방문하는 순서를 의미한다.
• BFS는 너비 우선 순회로 한 정점의 주변을 먼저 확인하는 방식
• DFS는 깊이 우선 순회로 한 정점으로부터 이어진 정점을 쭉 확인한 뒤, 그 주변을 순회하는 방식

- 너비 우선 순회 (BFS)

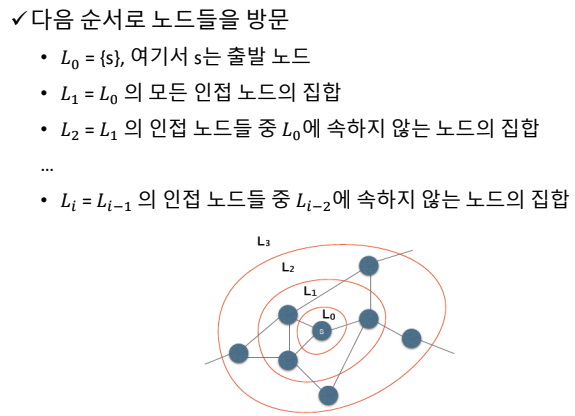
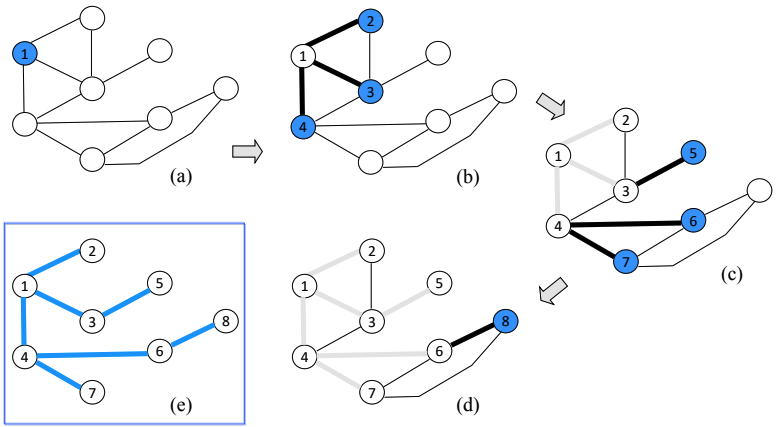
→ 마지막 트리의 모습을 너비 우선 트리라고 함

• 큐를 이용한 너비 우선 순회

  1. Check the start node;

  2. Insert the start node into the queue;

  3. while the queue is not empty;
     

     3.1. remove a node ‘v’ from queue;
     

     3.2. for each unchecked neighbor ‘u’ of v do
     

     ​ 3.2.1. check and insert ‘u’ into the queue;

pseudo code

BFS(G, s){
  // s는 start node
  for each v ∈ V
    visited[v] ← NO;
  	// visited : 방문 여부 확인 변수
  visited[s] ← YES;
  enqueue(Q, s);
  
  while(Q not empty){
    u ← dequeue(Q);
    for each v ∈ L(u){
      // L(u) : 정점 u의 인접 노드 집합
      if (visited[v] = NO) then{
        visited[u] = YES;
        enqueue(Q, v);
      }
    }
  }
}

- 깊이 우선 순회 (DFS)

• 개념적 이해
  1. 출발점 s에서 시작
  2. 현재 노드를 visited로 mark하고 인접한 노드들 중 unvisited 노드가 존재하면 그 노드로 간다.
  3. 2번을 계속 한다. → 아래로 쭉~ 내려간다.
  4. unvisited인 이웃 노드가 존재하지 않는 동안 계속해서 직전 노드로 되돌아간다.
     → 아래까지 쭉 갔다가 다시 올라온다. 끝까지 안 올라올 수도 있음!
  5. 2번을 계속한다.
  6. 시작 노드 s로 돌아오고 더 이상 갈 곳이 없으면 종료한다.

pseudo code

DFS(G){
  for each v ∈ V
    visited[v] ← NO;
  for each v ∈ V
    if(visited[v] = NO) then aDFS(v);
}

aDFS(v){
  visited[v] ← YES;
  for each x ∈ L(v)
    if (visited[x] = NO) then aDFS(x);
}

Queue

- 개념

• 컴퓨터의 기본적인 자료구조의 한가지로, 먼저 집어 넣는 데이터가 먼저 나오는 FIFO 형태의 자료구조
• Put, Insert, Enqueue
• Get, Delete, Dequeue
• Front, Rear
• Overflow, Underflow
• Linear Queue, Circular Queue, Linked Queue …
  

- Implementation Methodology

1. Linear Queue

   • 흔히 알고 있는 큐의 모습

   • front와 rear 변수를 사용해서 ENQ, DEQ 연산을 수행하게 됨
     

     → 비어 있을 때, front와 rear는 0
     → DEQ 시, front 하나 상승
     → ENQ 시, rear 하나 상승

   • rear가 size에 다달았을 때, FULL임을 나타내지만, front가 1이 아닐 수도 있음 → 이 문제를 해결하기 위해 Circular Queue 등장
     

2. Circular Queue

   • 값을 삽입할 때, 비어있는 공간도 채울 수 있도록 mod 연산을 적용 → 순환식
     

3. Linked Queue