Convex set (1)
Convex Optimization 포스트는 위 책을 참고해서 작성했습니다.
이 외에도 참고한 사이트는 다음과 같습니다.
저한테는 어려워서 이해한 만큼만 작성했습니다….
https://convex-optimization-for-all.github.io/ (모두를 위한 컨벡스 최적화)
Introduction
- 이제부터 Convex optimization에 대해서 포스트를 정리할 것이다.
- 이를 위해, 기본적으로 알아야 할 Convex set에 대해서 먼저 정리해보자!
What is Optimization problem?
-
Optimization problem은 다음과 같이 정의될 수 있다.
Finding the optimal solution or a solution close to optimal solution from multiple candidates.
-
수학적으로 정의한다면 다음과 같이 표현할 수 있다.
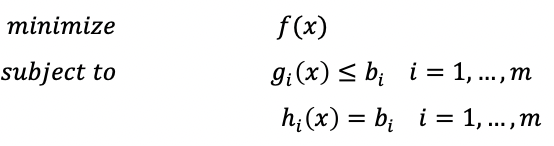
→ 그럼 여기서, Candidate가 f, g, h 함수들의 “정의역”임을 알 수 있다. -
이제 Optimization problem이 무엇인지 알았으니 앞에 붙어 있는 이상한 convex가 누군지 알아보자.
→ Optimization problem의 한 유형이다 ㅋㅅㅋ…
- 정의역이 convex이고, 목적 함수(f)가 convex function일 때, 우리는 문제를 convex optimization problem이라고 할 수 있다.
- Convex function은 다음 장에서 다룰 것이고, 지금은 정의역이 convex가 될 상황을 알아 볼 것이다.
Line, Line segment, Ray
- 각각은 직선, 선분, 반직선이다. 수학적 정의는 다음과 같슈
| Line | Line segment | Ray |
|---|---|---|
 |
 |
 |
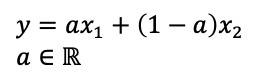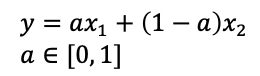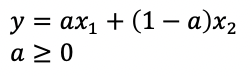- 직선은 두 점을 이으면서, 양 옆으로 끊임없이 나아가는 선을 의미한다.
- 선분은 두 점을 잇되, 딱 그 두 점만 잇는 선을 의미한다.
- 반직선은 직선의 개념과 비슷한데, 한 쪽으로만 끊임없이 나아가는 선을 의미한다.
- 그림으로 본다면 더욱 직관적으로 이해할 수 있다.
→ 각 직선, 선분, 반직선을 의미하게 된다. 뒷 내용을 스포하자면, 각각은 Affine, Convex, Cone set이 된다.
Affine, Convex, Cone set
Affine Set
Definition
-
정의는 다음과 같다.
→ 어떤 집합 C의 두 점 x와 y가 있을 때, 두 점을 이은 직선이 다시 집합 C에 속하게 된다면, 집합 C를 Affine Set이라고 한다. - 직관적으로 이해하기 위해 그림으로 한 번 봅시다.
→ 2차원 평면은 Affine set이다. 위의 정의를 생각해본다면 쉽게 도출할 수 있는 내용이다.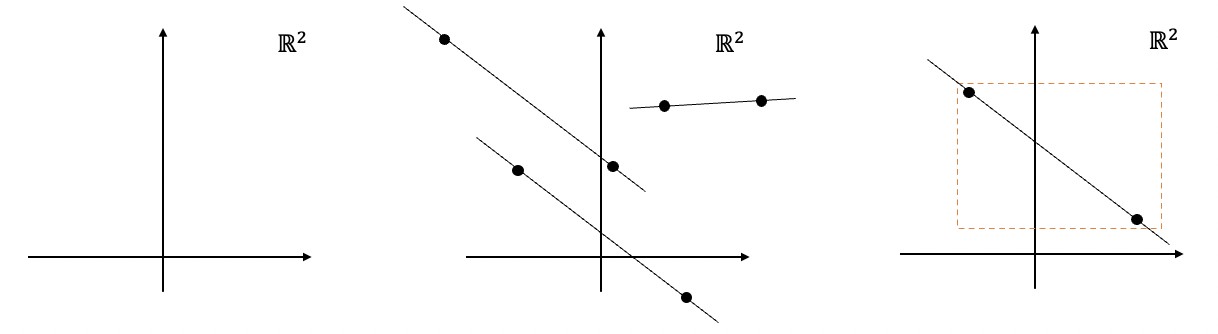
→ 우측의 그림과 같이 어떤 두 점을 이은 직선은 항상 2차원 평면 상에 속한다는 것을 알 수 있다.
→ 추가적으로 더 생각해본다면, 끝의 그림과 같이 경계가 있으면 Affine set이 될 수 없다. - 수식으로 한 번 더 이해해보자.
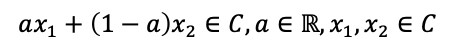
→ 앞서 나온 직선의 방정식을 생각한다면 왜 이렇게 나오는지 알 수 있다.
→ 식을 유심히 본다면, x 앞의 계수들의 합이 1이라는 것을 알 수 있다. 이를 활용해서 Affine comination을 만들 수 있다.
Affine Combination
- 집합에 있는 점들에 대해 Linear combination을 하되, 각 계수의 합을 1로 만든다면 그것을 Affine combination이라고 한다.
Affine Hull
- 어떤 집합 C에 속해 있는 모든 점들에 대해 모든 조합 가능한 Affine combination을 적용한다면, 그것을 Affine hull of C라고 한다.
Convex Set
Definition
- Affine과 매우매우 유사하다.
- 정의는 다음과 같이 할 수 있다.
→ 어떤 집합 C의 두 점 x와 y가 있을 때, 두 점을 이은 선분이 다시 집합 C에 속하게 된다면, 집합 C를 Convex Set이라고 한다.
→ Affine set의 정의에서 직선이 선분이 됐음을 인지하자. - 직관적으로 이해하기 위해 다음과 같은 그림을 생각해보자.
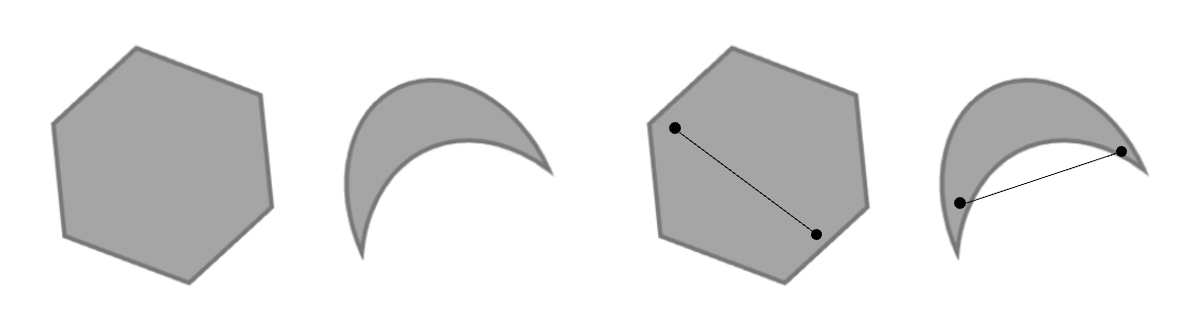→ 육각형은 어떠한 선분을 만들었을 때, 그 선분이 다시 육각형에 속함을 알 수 있다.
→ 달 모양의 경우, 파여있는 부분이 있기 때문에 어떤 선분은 다시 속하지 않음을 알 수 있다.
Convex Combination
- 선분의 수학적 정의에 따르면, 각 계수의 합은 1이 되면서 각 계수가 [0, 1]의 범위에 있다는 것을 알 수 있다.
- 이를 활용해서, 다음과 같이 Convex Combination을 정의할 수 있다.
→ 어떤 집합에 속해 있는 점들에 대해 Linear combination을 진행하되, 각 계수의 합이 1이 되고 각 계수가 [0, 1]의 범위를 갖도록 한다면 이를 Convex combination이라고 한다.
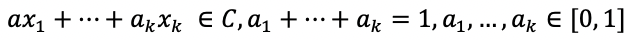
Convex Hull
- 어떤 집합 C에 속해 있는 모든 점들에 대해 모든 조합 가능한 Convex combination을 적용한다면, 그것을 Convex hull of C라고 한다.
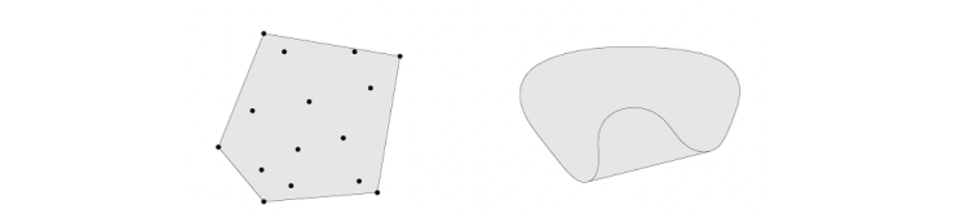
- 왼쪽의 그림을 보면 검은 색 점들만 있는 것이 원래 집합 C라고 한다면, 각 점들에 대해 모든 조합 가능한 Convex combination을 진행한다면 음영처리된 5각형이 나올 것이다.
- 오른쪽의 그림을 보면 고인돌(?) 모습이 원래 집합 C라고 한다면, 각 점들에 대해 모든 조합 가능한 Convex combination을 진행한다면 둥그런 모습이 나올 것이다.
- 따라서, Convex set이 아닌 집합에 대해 모든 조합 가능한 convex combination을 진행한다면, convex hull of C는 항상 convex set이 되게 된다.
→ 이는 이전에 나온 Affine hull에 대해서도 적용된다.
Cone
- 정의는 다음과 같이 할 수 있다.
→ 어떤 집합 C의 두 점 x와 y가 있을 때, 두 점을 이은 반직선이 다시 집합 C에 속하게 된다면, 집합 C를 Cone Set이라고 한다. - 수학적으로는 아주 간단하게 정의될 수 있다.
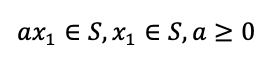
- Convex cone에 대해서는 다음 포스트에서 다루겠다.