Convex set (2)

Convex Optimization 포스트는 위 책을 참고해서 작성했습니다.
이 외에도 참고한 사이트는 다음과 같습니다.
저한테는 어려워서 이해한 만큼만 작성했습니다….
https://convex-optimization-for-all.github.io/ (모두를 위한 컨벡스 최적화)

Convex Cone

• 이전 포스트를 통해서 Affine, Convex, Cone에 대해서 배웠다.
• 이번 포스트에서는 Cone 중에서 Convex Cone에 대해서 배워볼 것이다.

Definition

• 수학적으로 Convex cone은 다음과 같이 정의된다. (반직선 정의를 다시 떠올려 보자)
  
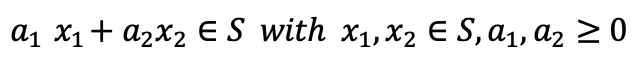
  → 해석을 해보자면, 어떤 집합 S에 속해있는 두 점에 대해서 만든 반직선이 다시 집합 S에 속하게 되면, 집합 S를 Convex Cone이라고 한다.
• 직관적으로 이해하기 위해 그림을 살펴보자.
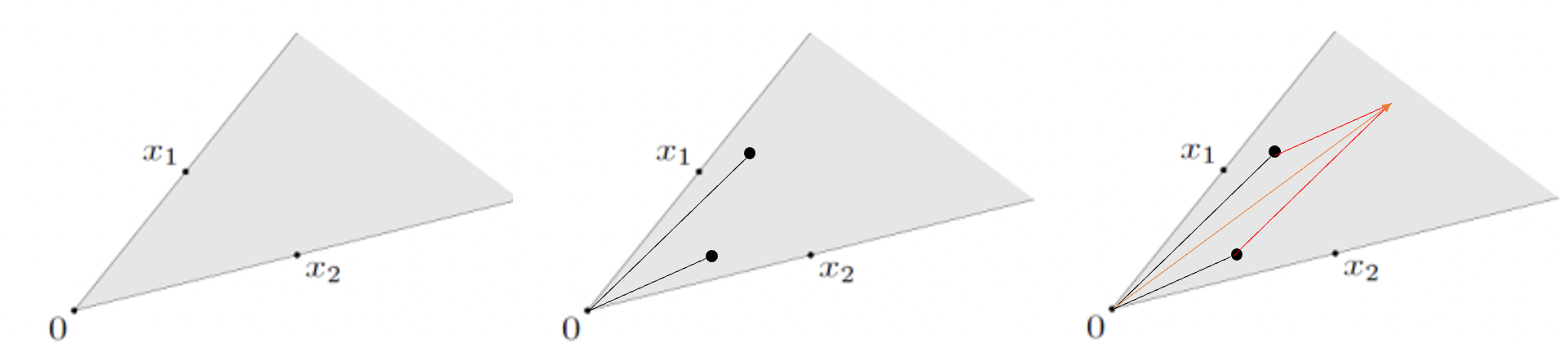  → 중간의 그림과 같이 임의의 두 점을 사용해서 반직선을 만든 상황이다.
  
• 이를 사용한다면, 이전에 계속 했던 Convex cone combination 또한 만들 수 있다. (계수가 0보다 클 때)

Example of Convex set

• 몇 가지의 대표적인 convex set의 예제를 확인해보자.

1. Hyperplane

• Hyperplane은 n차원의 공간을 반으로 가르는 n-1차원의 공간을 의미한다.

• 수학적으로는 다음과 같이 정의된다.
  

  
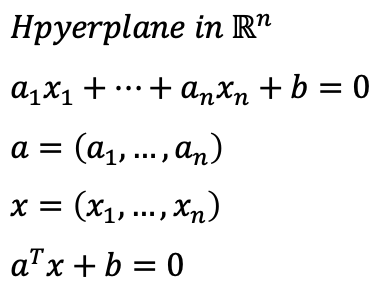
  → 3차원의 Hyperplane은 정의에 따르면 2차원의 공간, 면이 되게 된다.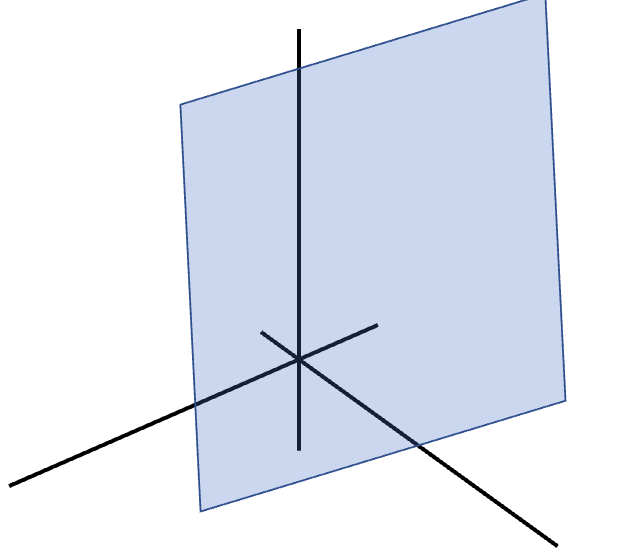
  
  → 이 예제에서 본다면 일단 경계가 없고 무한히 뻗어가는 공간임을 알 수 있다. 따라서 3차원의 Hyperplane은 Affine & Convex이다.
  
  

2. Euclidean Balls

• 유클리디안 볼의 정의는 다음과 같다.
  
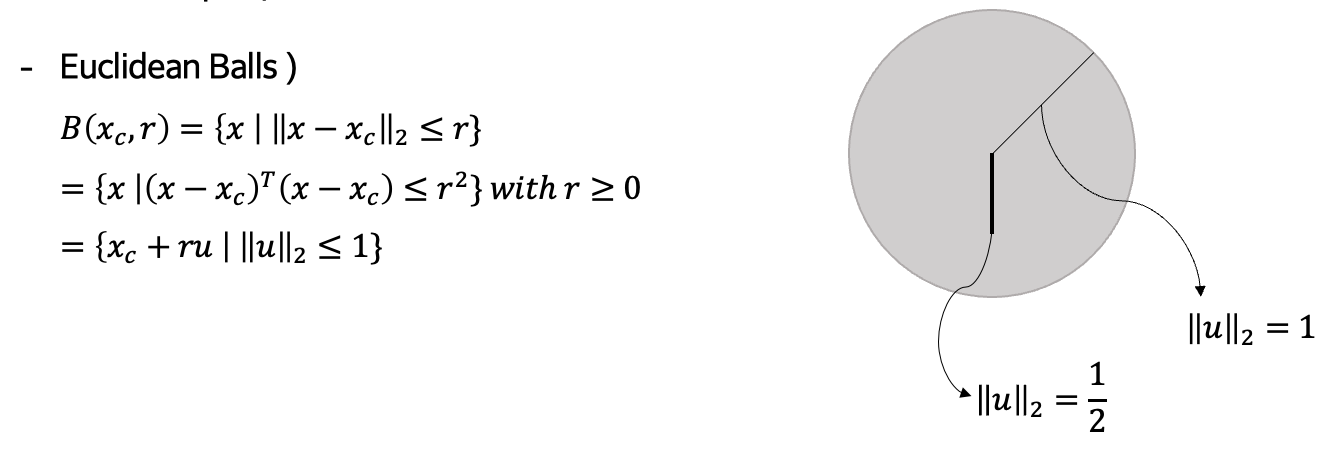
• 이는 Convex set인데, Convex의 정의를 사용한다면 쉽게 증명할 수 있다.
  
  

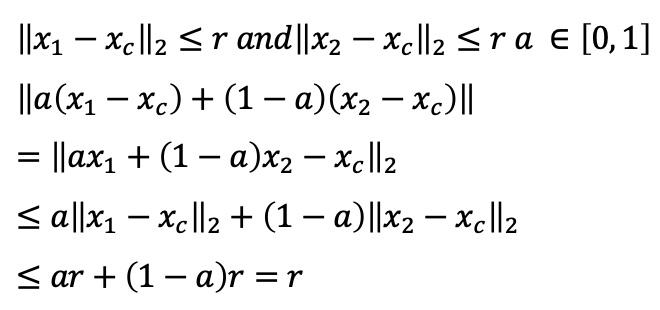
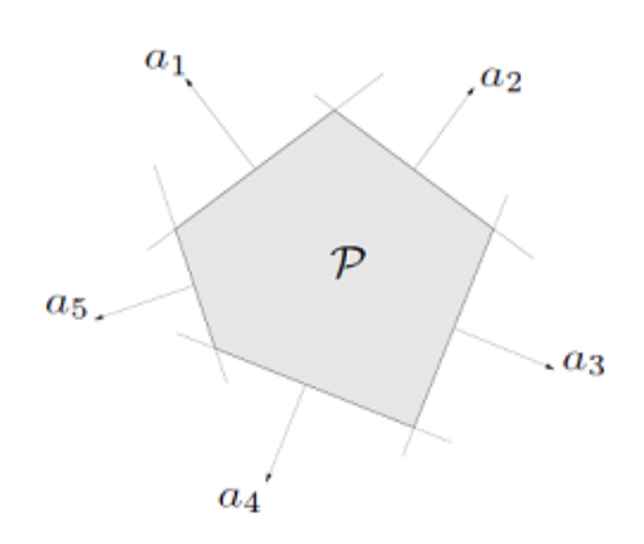
3. Polyhedra

• Polyhedra는 n차원 공간의 hyperplane들의 교집합을 의미한다.
• 어찌보면 당연하다고 느낄 수 있지만 뒤에 나올 convex의 교집합은 convex이다와 꽤나 관련있다.
  → hyperplane도 convex였으니, 교집합도 convex이다.
  
  
  

Example of Convex Cone

1. Norm Cone

• Norm cone은 n차원의 점들 중 t라는 반경 안에 존재하는 점들의 집합을 의미한다. 그림과 수식으로 보면 이해가 더 편하다.
  

  
  
  

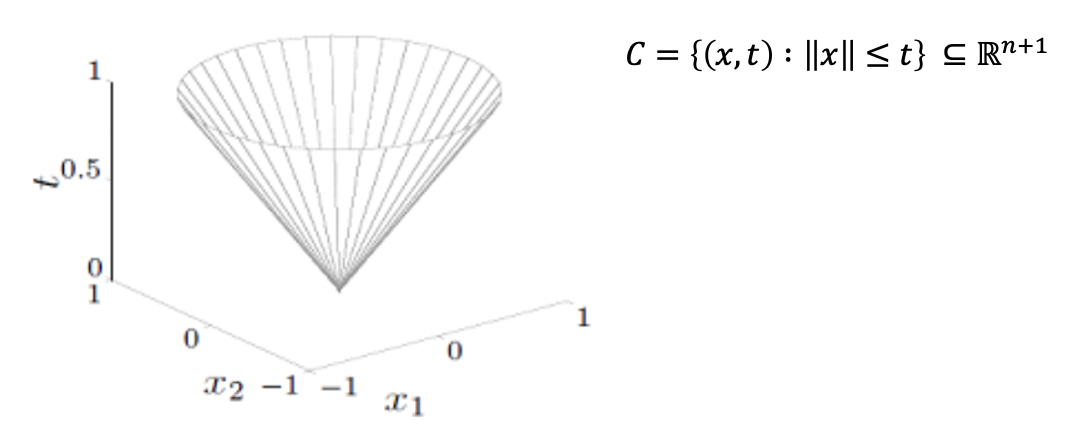
2. Normal Cone

• Normal Cone의 정의는 다음과 같다.
  
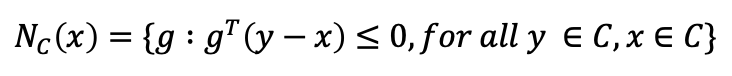
  → 즉, 어떤 집합 C에 대한 Supporting Hyperplane들의 집합을 의미한다.
  → Supporting Hyperplane은 일종의 접선 개념이다.
• 접선이라 하면, 어떤 집합 C와 어디서 만나는지가 중요할 것이다.
  
  
  

3. Positive Semidefinite Cone

• Positive Semidefinite Cone의 정의는 다음과 같다.
  

  
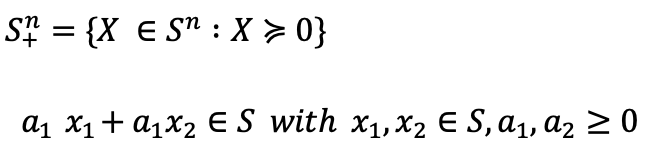
  → 즉, 집합 S에 있는 모든 점들은 0 이상의 정수 값을 갖고 있다는 것을 의미하고,
  → S는 Convex cone의 정의를 만족할 경우를 의미한다.
  
  

Operations that preserve convexity

• 다음으로는 집합의 convexity를 유지하는 연산에 대해 알아볼 것이다.

1. Intersection

• 앞서 살짝 언급했던 것이다.
• Convex set의 교집합은 Convex set이다.
  
  

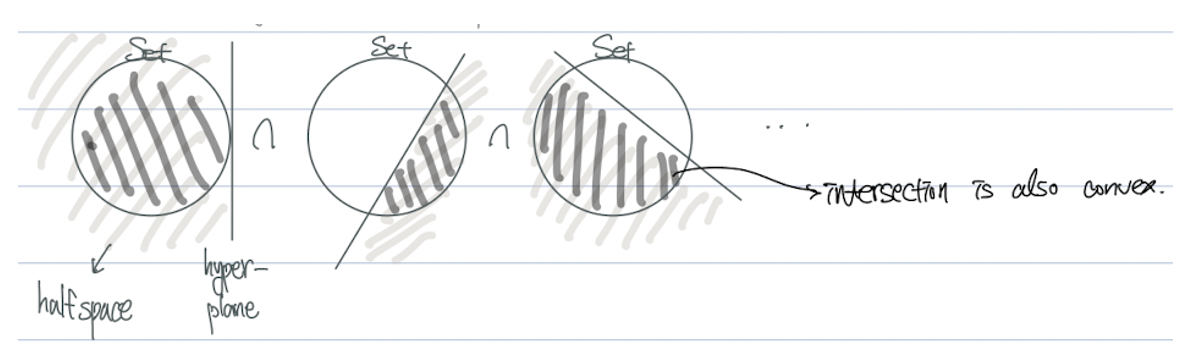
2. Affine function

• Affine function은 일종의 함수로서, 다음과 같이 정의될 수 있다.
  
  

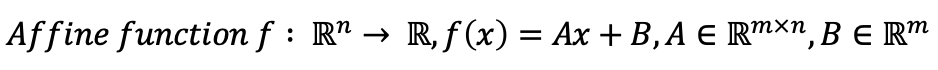
  → Affine function의 역함수 또한 동일하게 동작한다.
  → 대표적인 예시로는 Scaling and translation, projection, sum of two sets…등이 있다.
  

  
  

3. Respective function

• Affine function의 예시였던 projection function이다.
• 수식으로는 다음과 같이 정의가 되고,
  
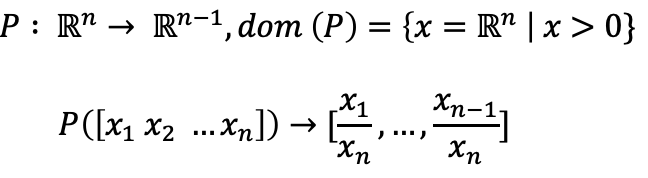
  → 하나의 차원을 낮춰주는 역할을 하는 함수다.
  

4. Linear fractional function

• Linear fractional function은 affine function과 perspective function의 결합체이다.
• 수식으로는 다음과 같이 정의가 되고,
  
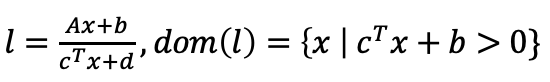
  → C=0 이고 d > 0이라면 함수 l은 Affine function이 된다.