Generalized inequality

Convex Optimization 포스트는 위 책을 참고해서 작성했습니다.
이 외에도 참고한 사이트는 다음과 같습니다.
저한테는 어려워서 이해한 만큼만 작성했습니다….
https://convex-optimization-for-all.github.io/ (모두를 위한 컨벡스 최적화)

Generalized Inequality

• 우리는 정수 1과 2 중 누가 큰지 알고 있다.1인가?
• 그럼 n-차원의 공간에서는 어떤 점이 다른 점보다 어떻게 크다고 말할 수 있을까?
  → 이를 할 수 있도록 하는 것이 Generalized inequality라고 한다.
• 그럼 첫 번째로 proper cone에 대해서 알아보자.

Proper cone

• proper cone은 다음과 같은 세 가지 조건을 만족할 때 성립하는 cone이다.
  
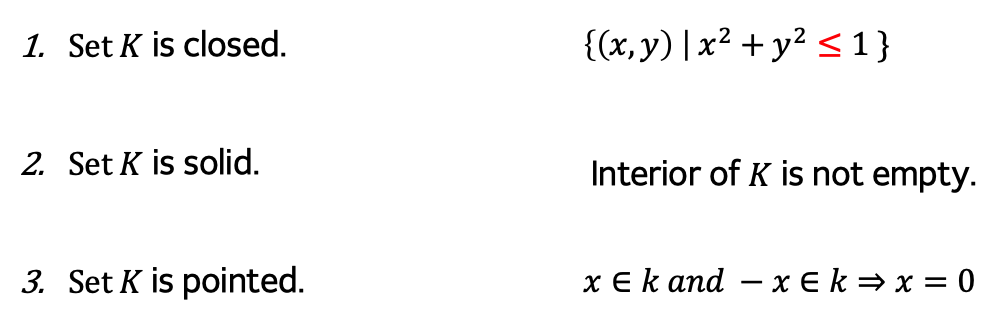
  → 마지막 조건은 원점을 지나되, 직선이 만들어 지지 않아야 한다는 것을 의미한다.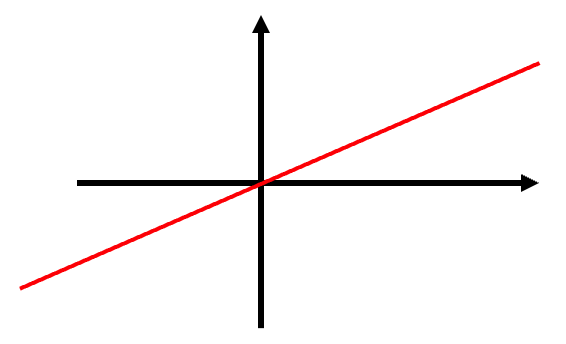
  
  

  → 즉, 이 상황이 나오면 안 된다는 것이다!
  
  

Definition

• 여기서는 “작다”의 개념이 아닌 “앞서 온다”라는 개념을 사용한다.
  
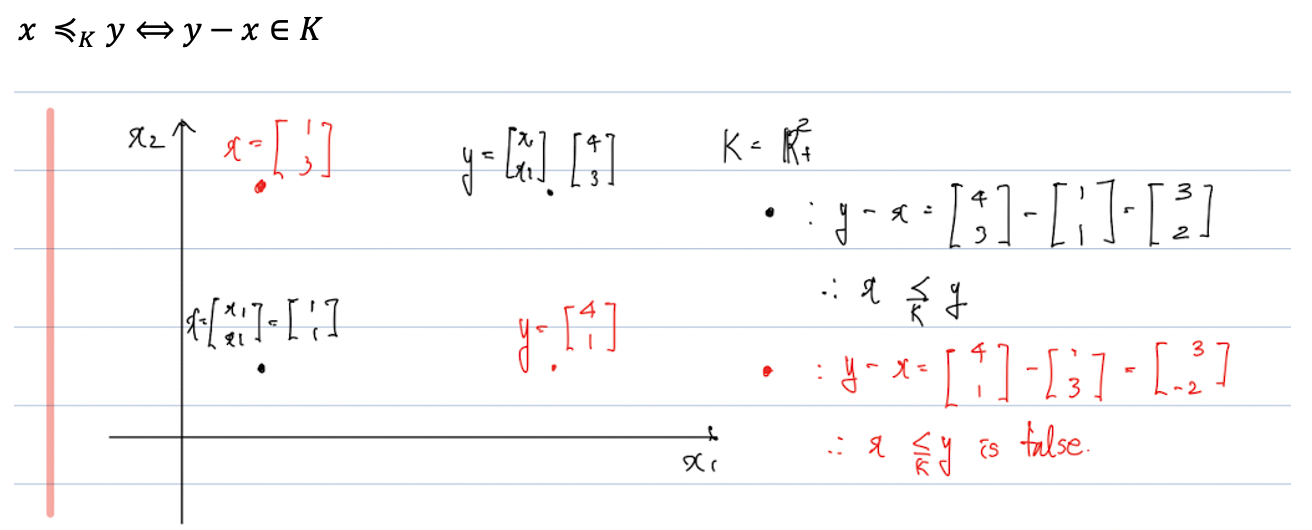
  → 부등호 밑에 첨자로 K가 있는 것을 알 수 있는데, 이 K가 proper cone일 때 성립하게 된다.
  → 즉, proper cone K 관점에서(in respect of) x가 y보다 앞서 온다. (검은 점)
  → 빨간 점은 부등호가 성립하지 않는 것을 확인할 수 있다.

• 또한 중요한 것은, 부등호(<)가 성립하지 않는다고 해서 그 반대(>=)가 성립하지 않는다는 것이다.

Minimum

• 다음으로 배울 내용은 minimum이다.

• Minimum의 정의는 다음과 같다.

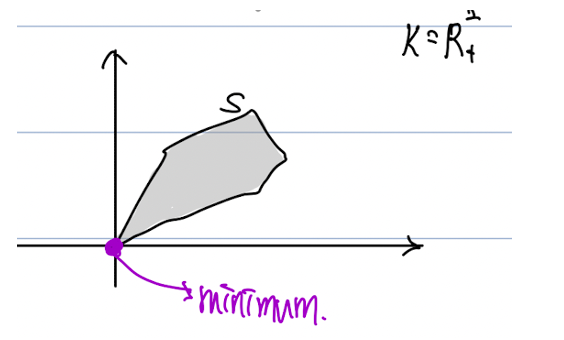
  어떤 집합 S에 속해 있는 어떤 점 x와 모든 점 y에 대해서, 항상 x가 y보다 앞서 온다면 이 x를 minimum이라고 한다.
  

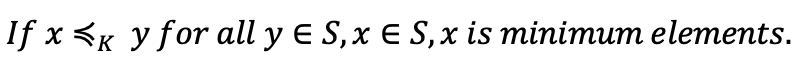
• 2차원 평면에서 생각해본다면, 어떤 집합에서 어떤 점을 기준으로 우측 상단으로만 집합의 원소들이 있다면 그 점이 minimum이다.
  
  

Minimal

• Minimum과 정의가 비슷하지만 조건이 살짝 다르다.

• Minimal의 정의는 다음과 같다.

  어떤 집합 S에 속해 있는 어떤 점 x와 모든 점 y에 대해서, y가 x보다 앞서 오는 상황이 x=y일 때만 발생한다면, x 점을 minimal이라고 한다.
  

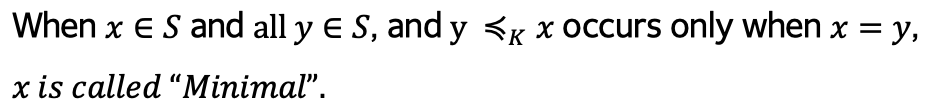
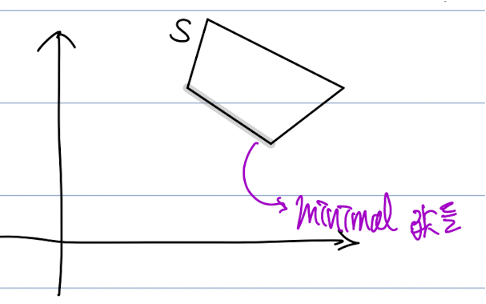
• 2차원 평면에서 본다면, x 점을 기준으로 좌측 하단에 집합 S의 점이 없을 때, x를 minimal이라고 한다.
  
  
  

Theorem

Separating hyperplane theorem

• 두 집합 C와 D가 있을 때, 그리고 C와 D가 non-empty disjoint convex set이라고 할 때, C와 D를 가르는 hyperplane이 존재한다는 이론이다.
  
  → 왼쪽 그림이 대표적인 예를 의미하고, hyperplane이 존재한다고 해서, C와 D가 non-empty disjoint convex set이 아닐 수 있다. 옆의 그림이 그 대표적인 예이다.
  
  

Supporting hyperplane theorem

• non-empty convex set C가 있고, boundary에 어떤 점 x0가 있다고 할 때, x0에서 항상 supporting hyperplane이 존재한다는 이론이다.

Dual Generalized Inequality

Dual Cone

• 먼저, Dual cone을 정의해보자.

• 이는 Cone으로부터 정의가 되고, 다음과 같은 조건을 만족하게 된다.
  
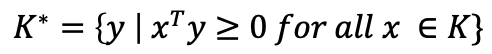
  → 내적의 정의를 생각해본다면, 사이각이 -90~90가 될 때를 의미한다. K는 cone을 의미한다.
  

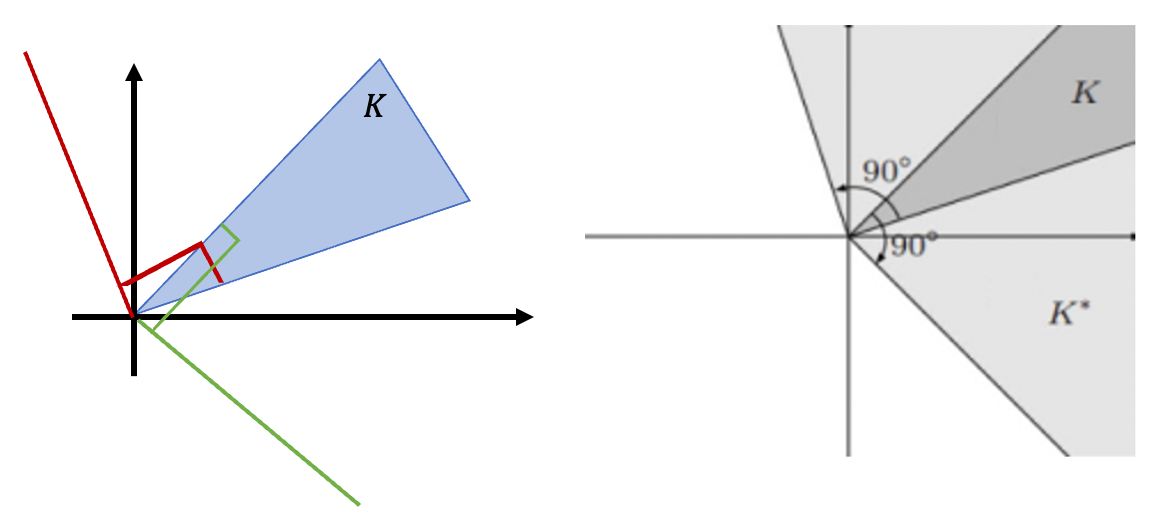
• 예제를 몇 개 살펴보자면,
  
  

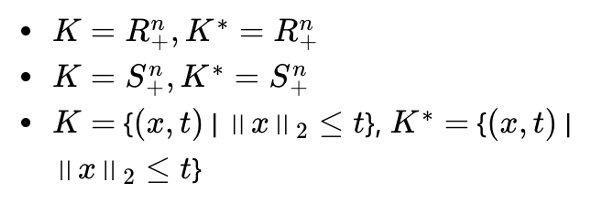
  → 각 예시들은 self dual cone으로, cone과 dual cone이 동일한 형태임을 의미한다.
  → 마지막 예제는 Norm cone이다. 그림을 보면 확실하게 이해할 수 있다.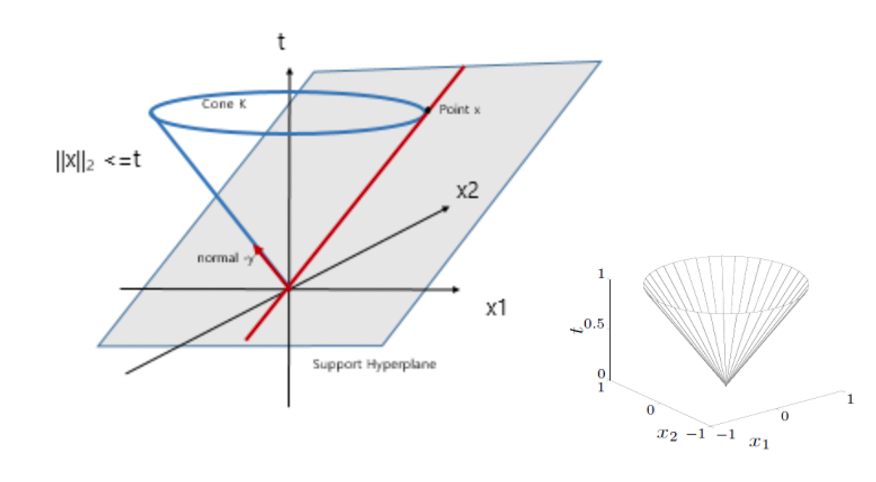
  

• 이 놈이 왜 중요한지를 보면, cone이 convex가 아니더라도 dual cone은 convex가 된다.

Definition

• 정의라기보다는 확장된 개념으로 이해를 하면 편하다.
  
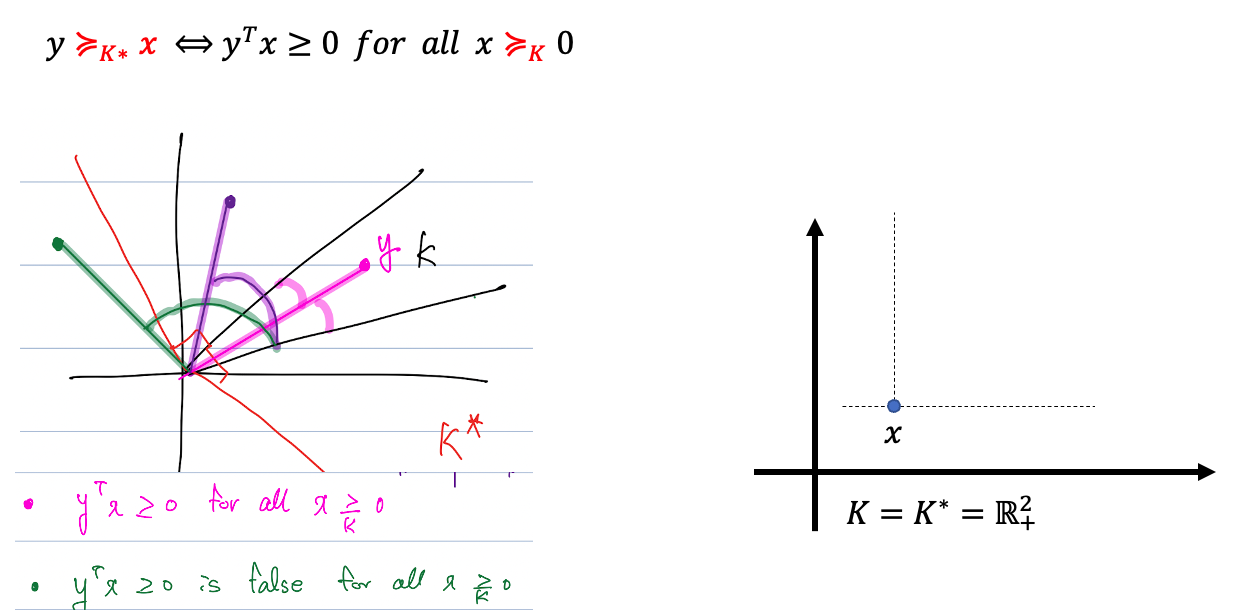
• 이에 대한 속성을 살펴보자면, lambda라는 하나의 값을 정의해서 확인할 수 있다.
  
  
  

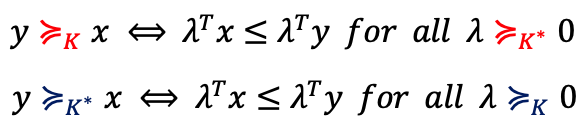
Mimimum

• 정의를 바로 확인하자.
  
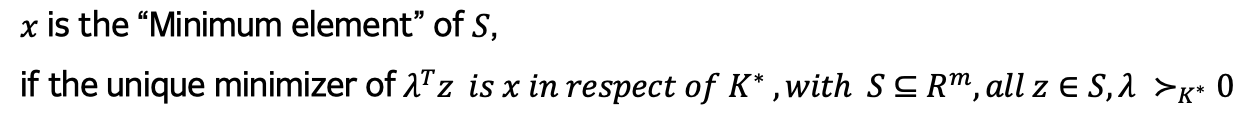
• 2차원 평면을 생각한다면, 쉽게 이해할 수 있다…(?)
  
  
  

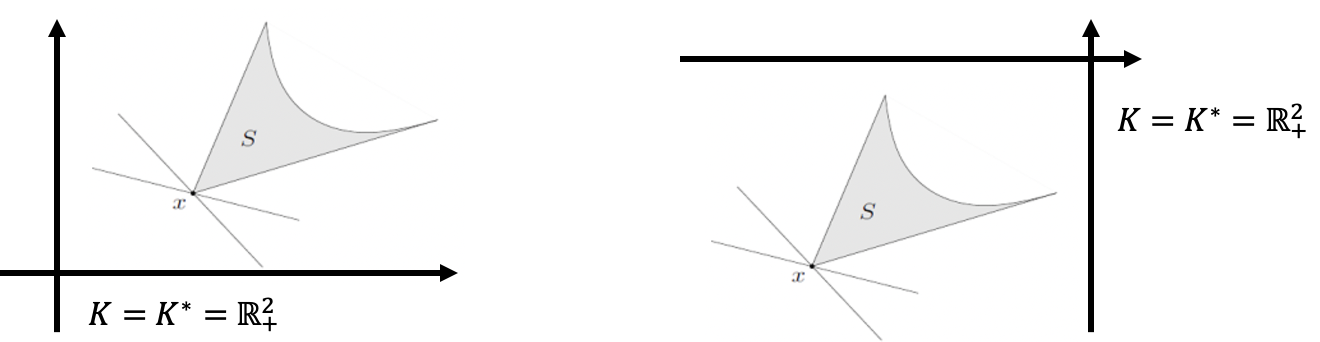
Minimal

• 요놈도 정의를 바로 확인하자.
  
  

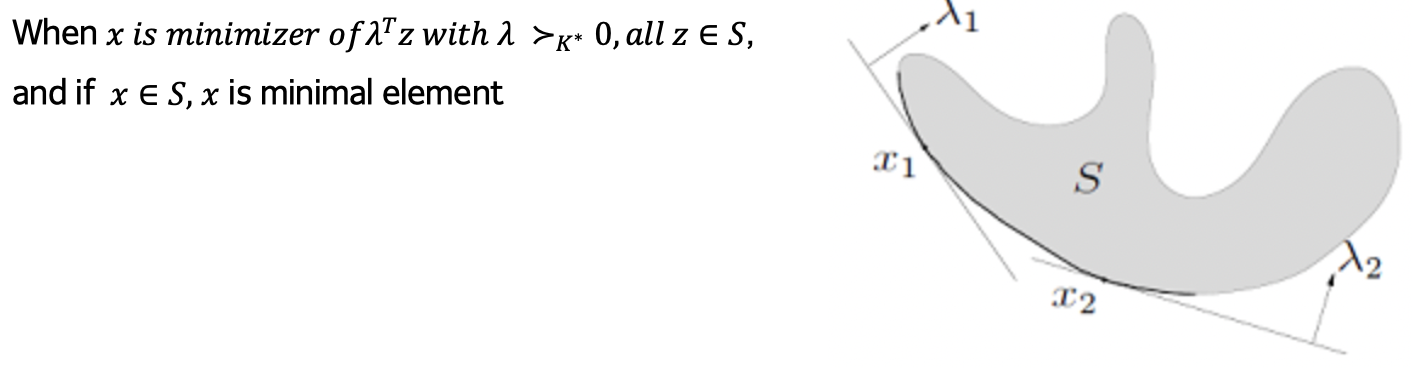
Example

• 실제 예제를 한 번 보면서 optimization problem에서의 적용법을 보자.
  
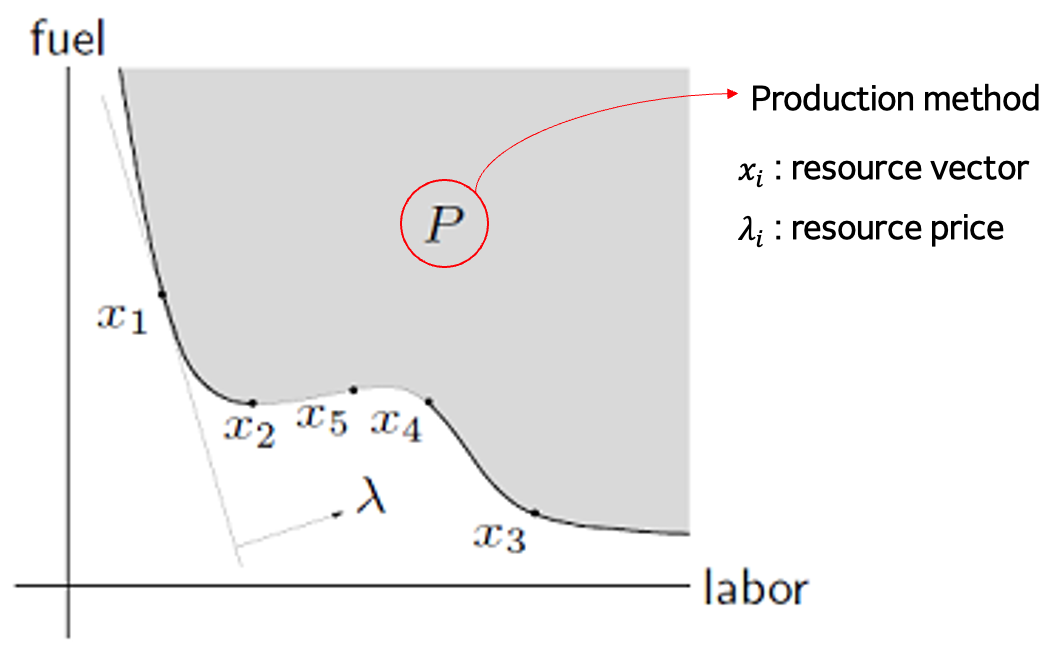
  → P를 생산 방법의 집합이라고 하면, 집합의 원소를 구성하는 벡터는 x로 연료(fuel)와 노동(labor)이라고 해보자.
  → 여기서, 자원 가격을 lambda라고 할 때,
  
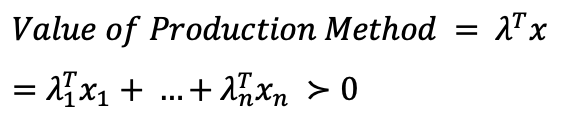
  → 그럼 생산 방법의 가격은 위와 같이 정의될 수 있다.
  → 가격을 최소화 하는 방법을 minimum을 찾는 것이라 할 수 있고, 최선의 방법을 minimal이라고 할 수 있게 된다.
  → 따라서, x1, x2, x3, x4는 minimal이 될 수 있다.