Dive into Lyapunov

Lyapunov Optimization은 위 책을 참고하여 정리 되었습니다.

Meaning of Lyapunov optimization

• Lyapunov optimization이 정말로 뭘 하는 녀석인지 제대로 확인해보자. (내 역량이 안될수도?)
• 먼저, 이전 포스트에서 나온 Lyapunov drift function을 다시 확인해보자.
  
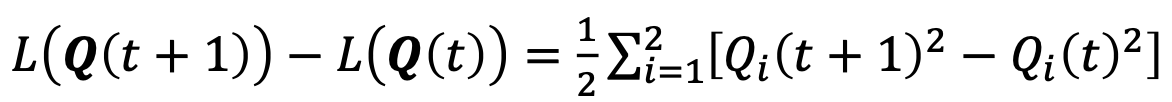
  → 사실 이 녀석은 Upper bounded될 수 있다.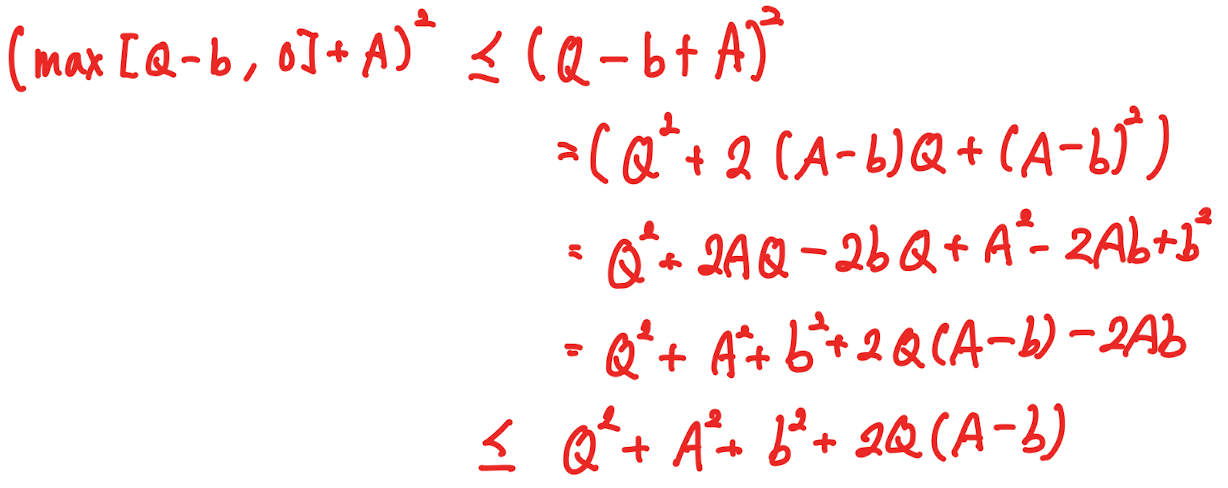
  
  → 구슬픈 나의 필기 실력을 기반으로,
  
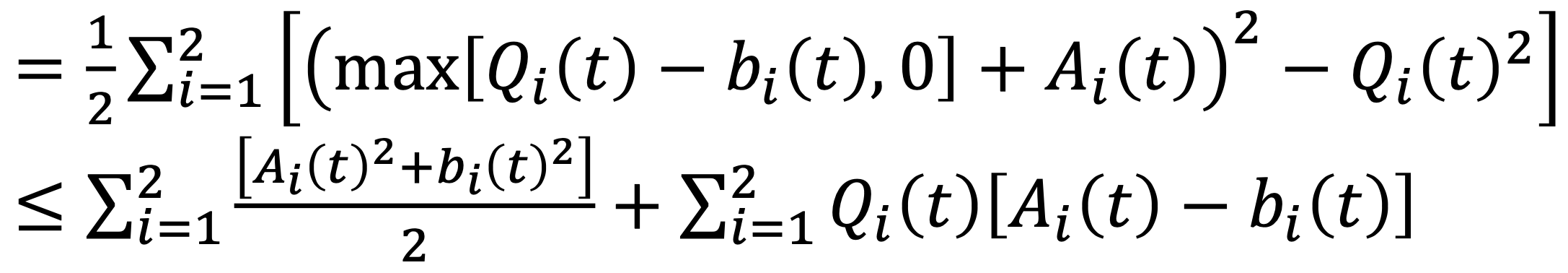
  → 다음과 같이 전개 후, upper bound를 제공할 수 있다.
  → cf) 부등호 바로 다음 term은 나중에 B라는 constant로 바뀔 수 있다.
  
  

Conditional Lyapunov drift function

• 추가적으로, Conditional Lyapunov drift function을 알아보자.

  • Conditional만 붙는다. 물론 의미는 있다.
    
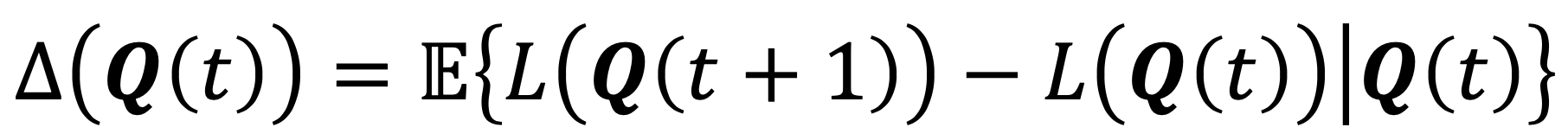
    → Arrival과 state 자체는 시스템 상에서 ‘확률적’으로 주어지기 때문에 expectation을 사용하여 표현할 수 있다.

  • 이 놈도 upper bounded 될 수 있다.
    → 위에서 적용한 방식을 그대로 사용한다.
    
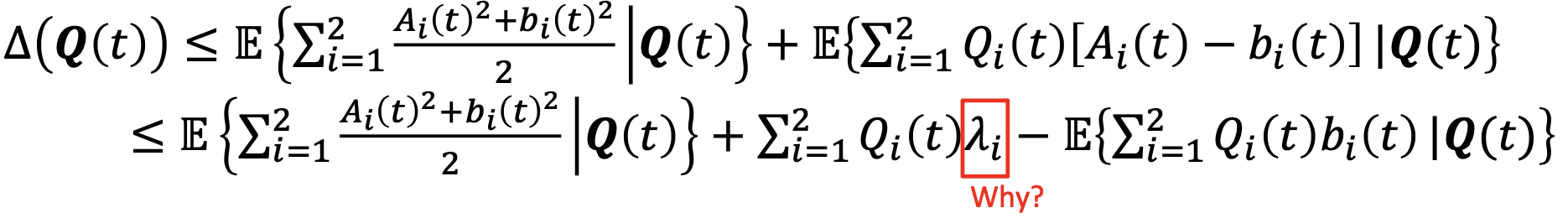
    → 여기서, 부등호 바로 앞 term은 B라는 상수로 치환될 수 있고, 붉은 색 람다 term은 나의 아름다운 필기를 보면 알 수 있다.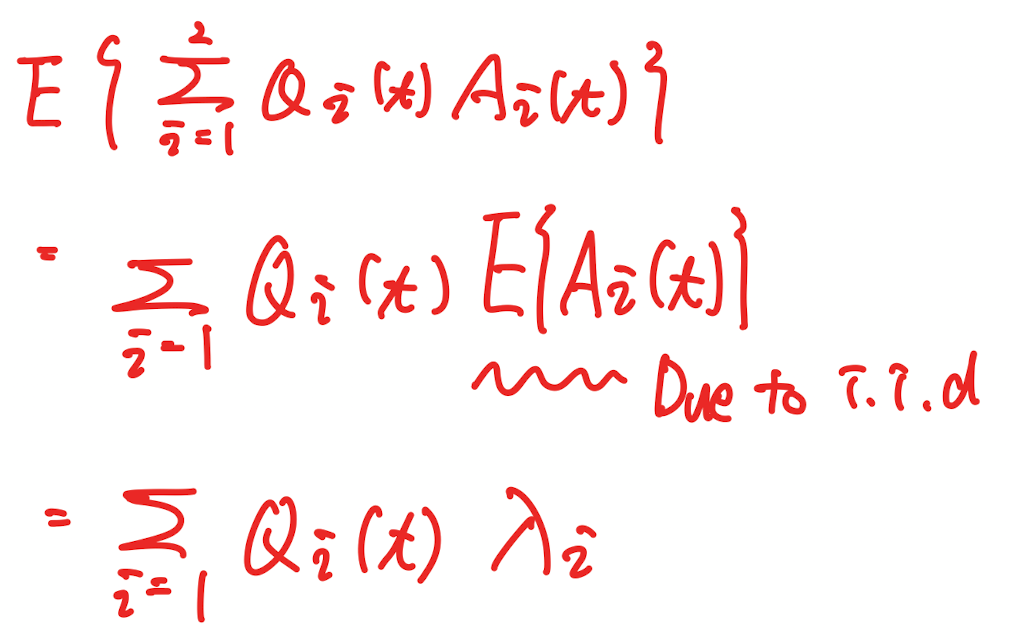
    
    → Lyapunov 의 강력한 assumption이 i.i.d.인 이유이다.

  • B는 도대체 뭔데?
    → arrival과 departure는 현실적으로 생각해보면 어떠한 한계점이 존재한다.
    → 당연하….다…? 네트워크라고 하면 한번에 무한대의 값을 받을 수 없고 무한대의 값을 처리할 수 없으니께
    → 그래서 한계점을 A_max, B_max라고 한다면,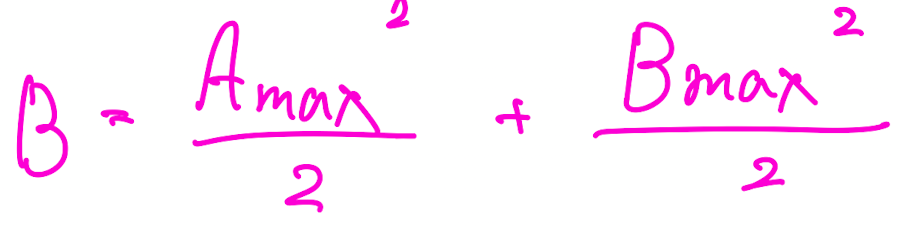
    

  • 그럼 이제 식을 이쁘게 바꿔보자.
    
    

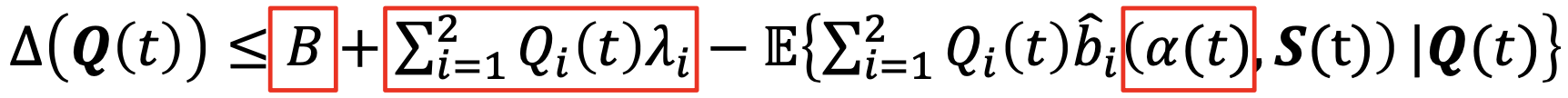
    → 각 박스를 숫자로 해서,

    1. B는 상수이므로, scheduling을 할 수 없다.
    2. Q(t)는 현재 시간에서는 주어졌지만, 평균 arrival은 control할 수 없는 값이다.
    3. 이것이 바로 우리가 control할 수 있는 scheduling 파라미터가 된다.

Minimization of upper bound

• 우리는 이전 포스트에서 Drift를 최소화하기로 했었다.
• 근데, 이제는 상한을 얻었으니 요놈을 최소화하면 결국 우리의 결과가 된다!
  
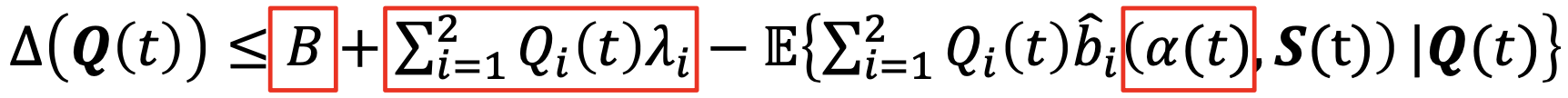
  → 그러면, 이 식에서 다시 생각해보자.
  1. 우리가 조절할 수 있는 파라미터는 α 값이다. 즉, scheduling indicator이다.
  2. 위 식을 minimization한다는 것은, α가 붙어있는 term을 maximization하게 되는 것이다. (빼기 붙어있음 ㅋㅋ)
• 정리하자면, 주어진 시스템 환경에서는 greedy 형태로
  
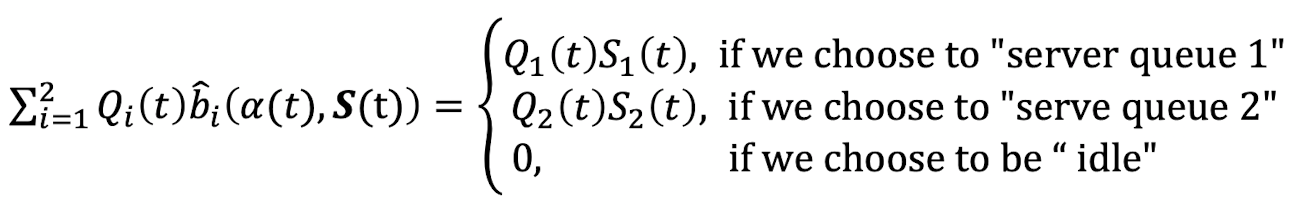
  → 와 같이 scheduling을 할 수 있게 된다.
  1. 각 time slot t에서는 Q(t)와 S(t)를 observe
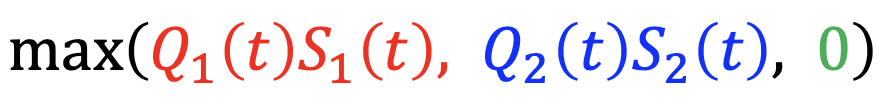  2. 에 따라 α를 결정
     → Queue * amount of departure가 큰 queue일수록 높은 우선순위를 갖게 됨을 의미한다.
• 그럼, 진짜 이렇게만 해주면 좋은 성능(stable)이 나올까?
  → 귀찮으니 다음번에 쓰겠다.