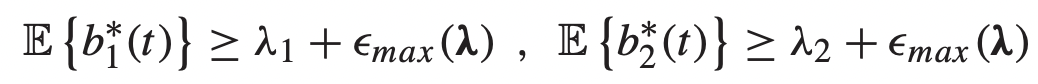Dynamic scheduling

Lyapunov Optimization은 위 책을 참고하여 정리 되었습니다.
혼자 공부하면서 쓴 내용이기 때문에 잘못된 내용이 있을 수도 있습니다…개강하면 수정할게요…

Dynamic Scheduling

• Dynamic scheduling은 후에 서술될 Lyapunov Drift 와 Lyapunov optimization으로부터 개발된 알고리즘이라고 할 수 있다.
• 이전 포스트와 동일하게, arrival rates와 channel state는 모두 알고 있다고 가정하지만, 현재 채널에 따라 결정되는 randomized scheduling algorithm이 아닌, minimizing the drift of a Lyapunov function을 기반으로 문제를 해결해 나갈 것이다.
  → 뭔 소린지 이해가 안 간다…….
• 이러한 것의 장점은 current channel states와 current queue backlogs를 시스템을 stable하게 만들기 위해 사용한다는 것이다.
  → 즉, priori knowledge는 필요하지 않다.
  
  

Scheduling For Stability

• 이전 포스트에서 사용했던 예제를 그대로 가져와서 한 번 확인해보자.
  
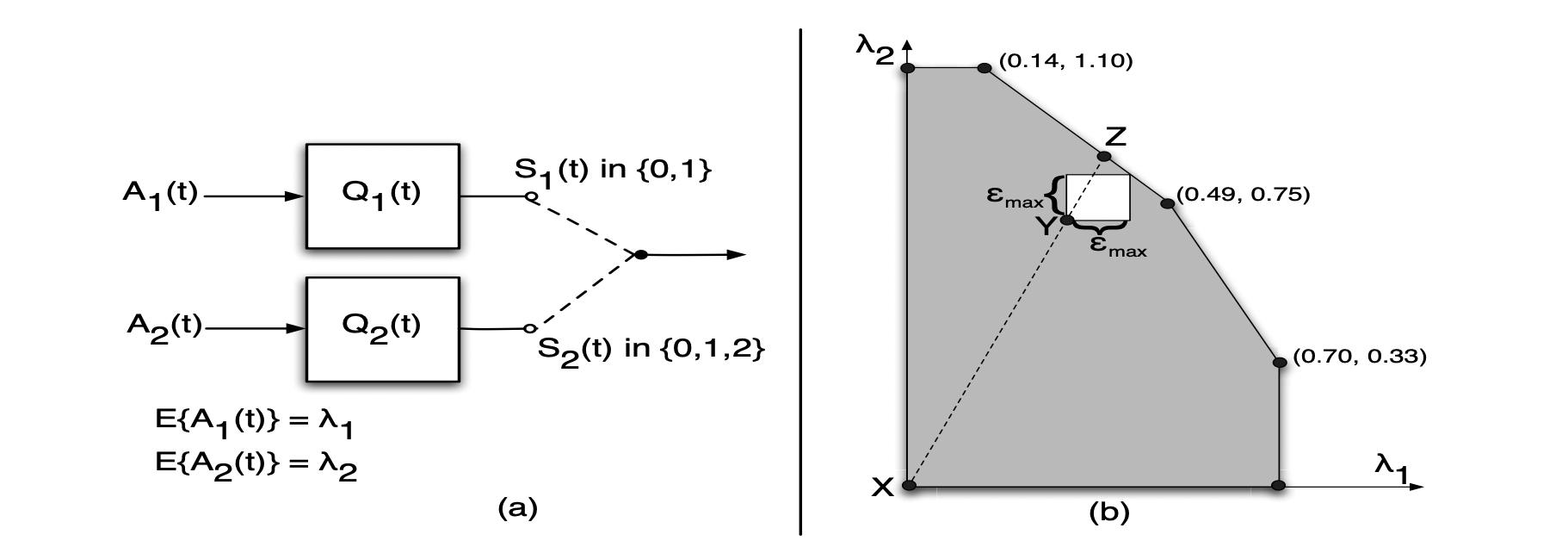
  → 각 입력 값(유입되는 패킷의 양)은 λ1과 λ2의 expectation 값을 갖는다.
  → 이로 인해서, 우측 그래프와 같이 Capacity region Λ가 생기게 된다.🍊

Environment

• 위에서 가정한 상황을 자세히 살펴보자.
• In every time slot t,
  • Arrival vector는 각각 A1(t), A2(t)로 정의되고, i.i.d.이다. 그리고 각각은 λ1과 λ2의 expectation 값을 갖는다(arrival rate).
  • Channel state vector는 S(t) = (S1(t), S2(t))로 정의된다. non-negative integer로 channel i에서 전송될 수 있는 패킷의 개수를 의미한다.
    
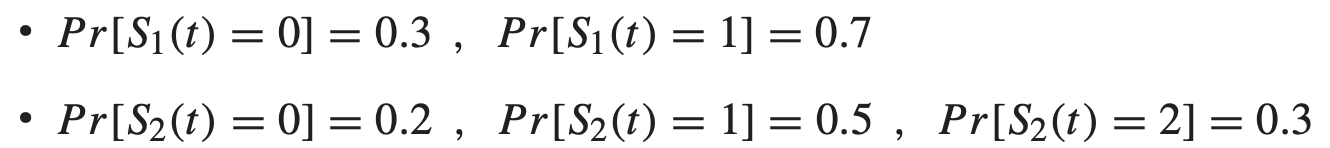
    → S1(t)와 S2(t)는 다음과 같은 확률을 갖게 된다.
  • Network controller는 S를 매번 확인한 뒤, transmission decision을 내리게 된다. 이는 α(t)로 표현한다.
    
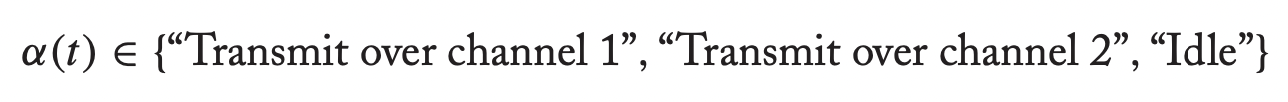
    → Idle은 당연히 아무것도 보내지 않을 때를 의미한다.
  • 위와 같이 정의된 변수를 기반으로 Queue를 디자인하면,
    
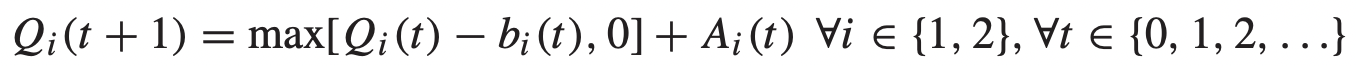
  • 아직 우리는 b(t)를 정의하지 않았다. 이는 다음과 같이 정의되고,
    
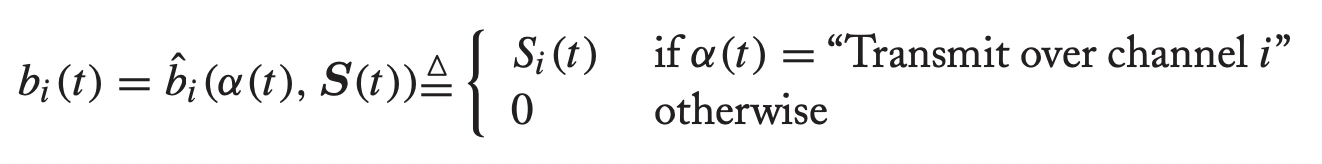
    → Channel state vector와 decision 값을 사용하게 된다. 즉, 선택이 되었을 때, 몇 개를 보낼 수 있는가
    

The S-only policy algorithm and ε-max (only channel S tate)

• Channel state vector는 다음과 같은 output을 가질 수 있다. 이를 S로 정의한다면,
  
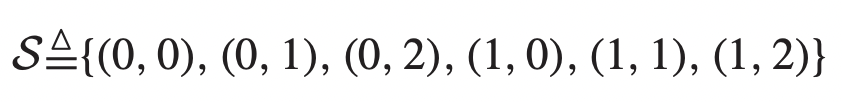
  → 이 놈을 사용한다면, independent, stationary, randomized transmission decision을 내릴 수 있을 것이다. (+ independent of queue backlogs)

• 이를 위해서, S에 의존하는 변수를 하나 더 생성하자.
  
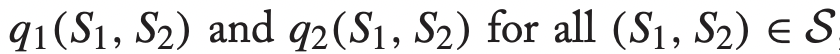
  → 이로써, q1과 q2는 the probability of transmitting over channel i if S(t) = (S1, S2)가 된다.
  

  → q1 + q2 <= 1 (채널은 아예 선택하지 않을 상황도 고려)

• S-only 에서 결정되는 α 값을 α* 라 하고 b 값을 b* 라고 한다면, 다음과 같이 정의가 될 것이다.
  → 즉, 어떠한 정책을 기반으로 정해지는 처리량과 채널 선택 여부이다. (이건 상수다.)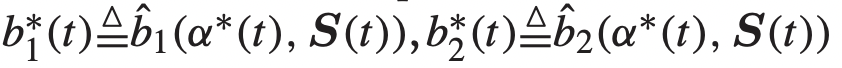

  
  
  → S-only policy를 통해 결정되는 b의 expectation은 다음과 같이 정의된다.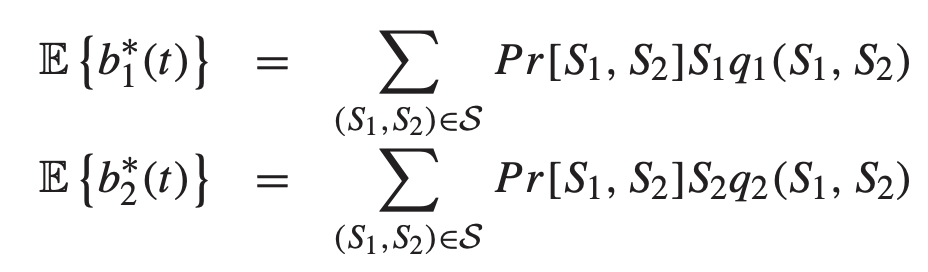
  
  
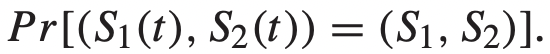
  → 한국어로 말하자면, (몇 개를 처리할 확률) * (몇 개를 처리할 수 있나의 몇 개) * (그 채널이 선택될 확률)이 된다.
  

ε-max

• 정책으로 값이 정해졌으니, 아래 식을 만족해야 한다.
  
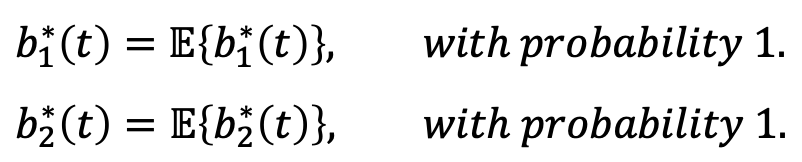
• 그리고, rate stability를 위해서,
  
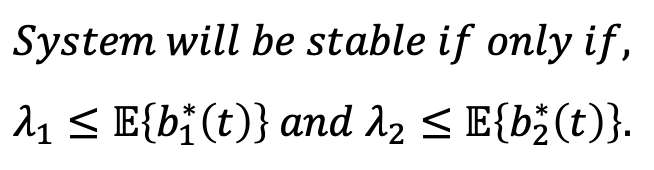
  → 앞서 정의한 λ1과 λ2는 위 식을 만족해야한다.
• 쉽게 생각하면, 무작정 transmission rate를 높이면 될 일이지만, 유입량을 생각해봤을 때, ε 값을 추가로 도입해볼 수 있다.
  
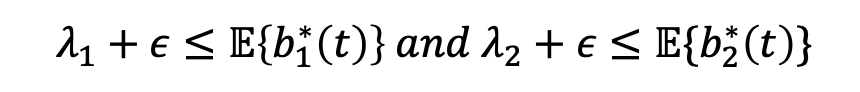
  → 짜잔. ε을 Maximize하는 문제로 변형할 수 있다.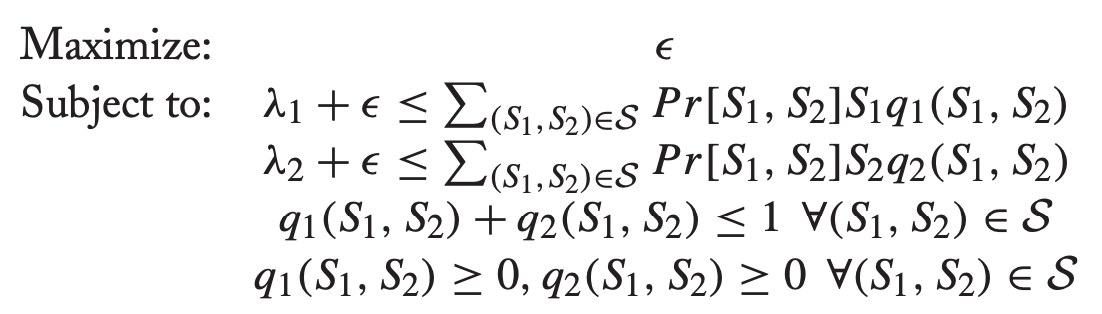
  
  

Maximize Problem

• 위 식에서는 known parameters와 unknown parameters가 있다.
  

  KNOWN	UNKNOWN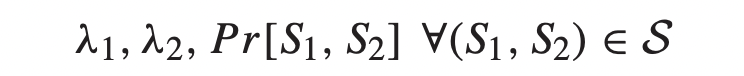

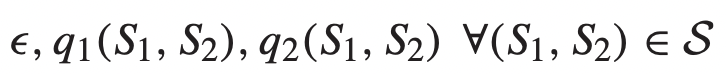
• 위 식의 optimal을 ε-max라고 가정했을 때, 이 값은 Capacity region Λ안에서 찾을 수 있게 된다.🍊
  → 그렇다면, ε-max는 현재의 λ와 Region Boundary까지의 거리가 될 것이다.
  → 더 나아갈 수 있는 여력(?)이라고 이해했다.
  → 그럼 추가로, λ가 interior of Capacity region에 있다면, ε-max는 0보다 클 것이다(0이 아니다).

• 그럼 그림에서의 예제로 다시 살펴보자.
  
  → 우측 그래프에서 Y점은 (0.3, 0.7)의 값을 갖고 있는 상황이고, boundary까지 거리는 0.12이다.
  → 즉, 이러한 방식을 통해서 다음 식을 만족하는 and policy를 만족하는 값들을 찾을 수 있다.
  → 예시를 하나 생각해본다면, router에 주는 power를 고정시켰을 때 유입량을 최대화하는 방법도 있다. (아닐수도?)