Introduction to Lyapunov

Lyapunov Optimization은 위 책을 참고하여 정리 되었습니다.

학기가 시작됐는데 귀찮아서 이제야 씁니다..

Lyapunov Optimization-based Algorithm

• 드디어 오늘 배울 내용은 Lyapunov Optimization 기법이다.
• 본격적으로 들어가기 전에, 이전에 배운 S-only policy와의 차이점은 무엇인지 생각해보자.
  • S-only policy에서 필요한 것은?
    
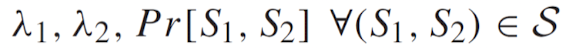
    → 평균 arrival rate와, state에 대한 확률적 정보이다.
  • 전혀 실용적이지 않다. arrival rate의 확률적인 값은 모르는게 더 많다.
• 그럼, 어떤 정보를 Lyapunov에서 필요로 할까?
  • 현재 time slot t에서의 arrival rate와 state이다.
    → 즉, 위에서 다룬 ‘평균’ 값이 아닌 현재 슬롯에만 관심이 있게 된다.
    → 더 명확히 말한다면, 매 순간 순간마다 시스템에서 관측할 수 있는 정보라고 할 수 있다.
  • 이 정보만으로 사실 전체 시간 관점에서의 Queue stable을 조절할 수는 없다.
    → 따라서, 앞서 계속 다뤘던 Queue 정보를 사용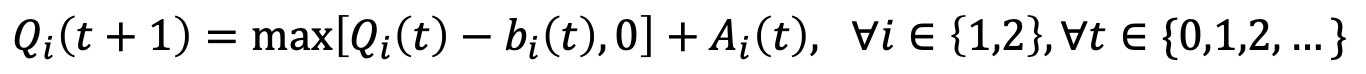
    
    → 이 식은 Magic of Queue라고 불리기도 한다.
    → Q(t)를 통해 t 시간 이전의 distribution을 알 수 있기 때문이라고 한다. 💩
    

Derivation

• 그럼, ‘어떻게’ 하는지에 대해 알아보자.

• 첫 번째로 만들어 내야 하는 것은 Lyapunov function이다.
  
  

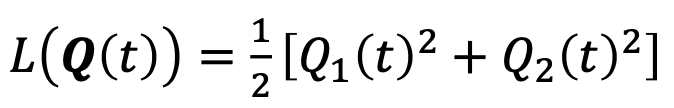
  → 식이 의미하는 바는 무엇일까?

  1. 단순히 생각한다면 각 Queue에 남아있는 작업량이라고 볼 수 있다.
  2. 제곱을 취함으로써, 남아있음을 ‘강조’한다. → ‘강조’의 의미는 뒤에서 다루도록 하겠다.

• 두 번째로는, Lyapunov function을 기반으로 Lyapunov Drift function(이하 drift)를 만드는 것이다.
  
  

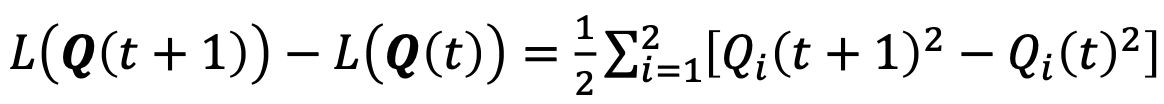
  → 즉, Lyapunov function의 변동성(drift)이라고 볼 수 있다.
  → 그러면, 이 drift를 최소화한다면 어떻게 될까?
  → 우리는 현재 상태만( L(Q(t)) ) 알고 있고, Q(t+1)은 Q(t)에서 arrival과 departure로 나눌 수 있다.
  

Minimization of Drift

• 간단한 예제 두 개를 보자.
  Example 1.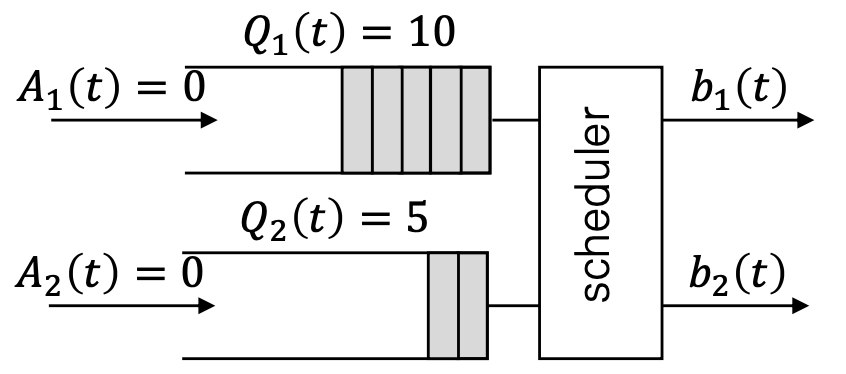
  

  • 
    → 현재 슬롯에서, arrival은 모두 0이고, departure는 모두 3, 그리고 Queue backlog는 각각 10과 5이다.
  • Queue 1이 스케쥴되었을 때, Drift :
    
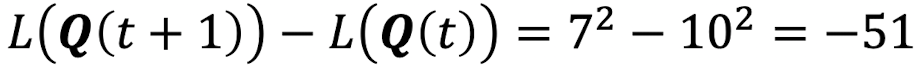
  • Queue 2가 스케쥴되었을 때, Drift :
    
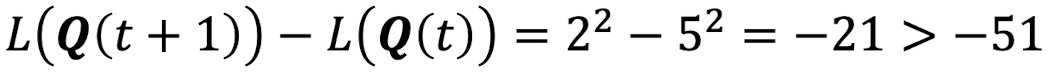
  • 아까 Drift를 minimization한다고 헀으니, Queue 1이 선택될 것이다.
    

  Example 2.

  • 
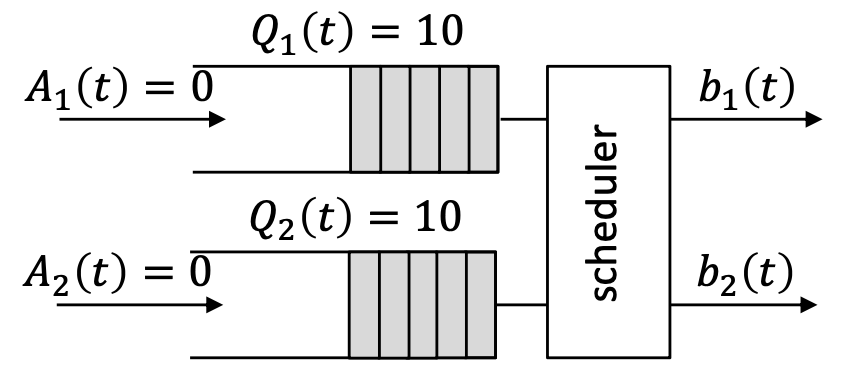
    → 현재 슬롯에서, arrival은 모두 0이고, Queue backlog는 모두 10, 그리고 departure가 각각 3과 2이다.
  • Queue 1이 스케쥴되었을 때, Drift :
    
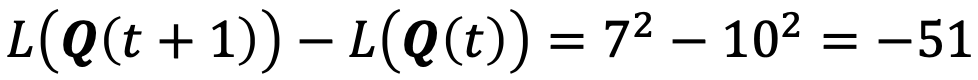
  • Queue 2가 스케쥴되었을 때, Drift :
    
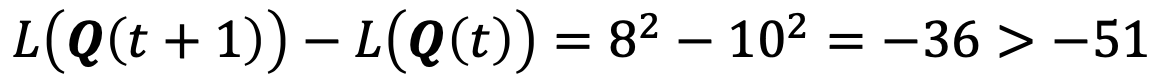
  • Minimization해야되니까, Queue 1이 선택된다.
    

Result

• 그럼 앞의 예제를 통해 내릴 수 있는 결론은 무엇일까?

• 각 예제별로

  1. Queue backlog(작업량)가 더 많이 남은 Queue에 더 높은 관성이 생긴다.
  2. Departure 양이 큰 Queue에 더 높은 관성이 생긴다.

• 즉, Drift를 Minimization하는 것이 위 두 결론을 통해 최종적으로 Queue를 stable하게 만들 수 있다고 느껴진다.
  

  → 계속 진행하면서, 결국엔 stable이 됨이 증명된다.