Introduction to Queue

3 minute read

Lyapunov Optimization은 위 책을 참고하여 정리 되었습니다.
혼자 공부하면서 쓴 내용이기 때문에 잘못된 내용이 있을 수도 있습니다…개강하면 수정할게요…

Introduction Queue

네트워크에서 Queue는 실제적인 환경을 표현하기 위해 사용된다.
여기서 네트워크는 timeslot마다 유입되는 일의 양과 이 일을 처리해서 보내는 라우터가 있다고 해보자.
→ 각각을 a(t)와 b(t)로 notation을 정의해보자.
우리가 정의한대로 한다면 다음과 같이 Queue를 표현할 수 있다.

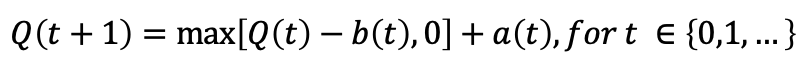
→ a(t) : the amount of new work that arrives at timeslot t.
→ b(t) : the amount of work that the router of the queue can process on timslot t.
a(t)와 b(t)가 “stochastic”하다고 하면, 어쩌면 모든 네트워크를 대변할 수 있을 것이다.
→ 그렇다면, a(t)와 b(t)가 어떤 RV로 모델링 되어야 한다는 것을 의미한다.
→ 즉, 미래의 상황까지 a(t)와 b(t)의 정보를 모두 알고 있다는 것을 의미한다.
위 내용을 그림으로 확인해 보자.

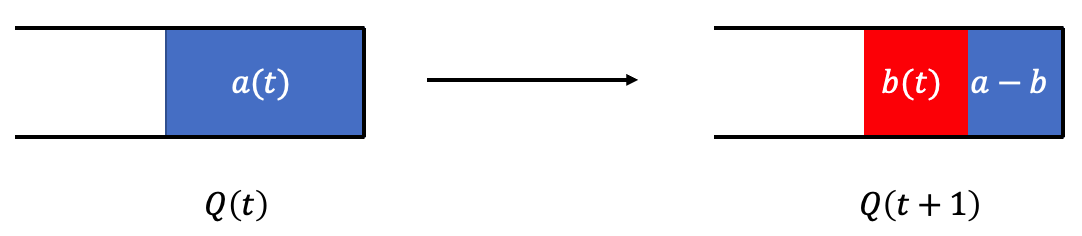
→ 여기서, Q(t)를 backlog라고 하고, 처리되어야 할 일의 양을 의미한다.

→ Backlog : the amount of work that should be processed.

b(t)를 우리는 확률적인 값으로 한다고 앞서 말헀다.
그럼 b(t)를 실제 일의 처리량이라고 생각해보자. b틸다로 표기할 것인데 특수 문자가 없다 ㅋㅅㅋ

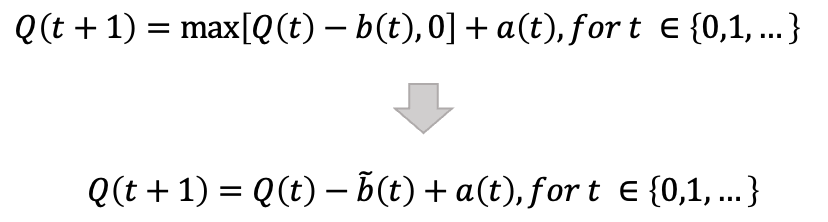
→ 실제 처리되는 일의 양은 확률 적인 값보다 낮을 것이기 때문에 max를 제외하고 화살표 아래와 같이 표현할 수 있다.
여기서, 식의 확장을 위해 두 개의 timeslot인 t1과 t2를 고려해보자.

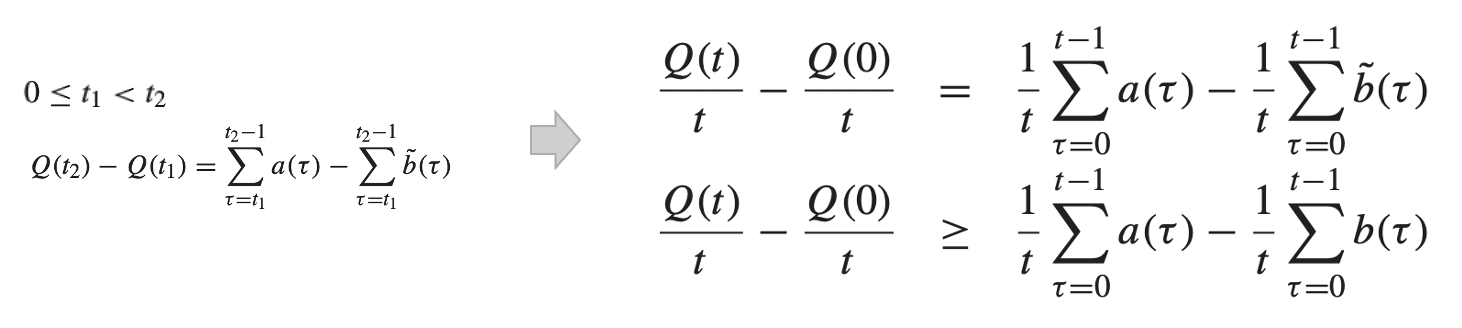
→ Queue는 시간의 연속에서 처리되는 형태이기 때문에, 화살표 왼쪽과 같이 표현을 할 수 있다.
- 먼저, 화살표 우측 상단의 식을 확인해보자.
  → t2=t, t1=0인 상황에 대한 식으로, 단순히 좌측 식에서 t로 나눈 상황을 의미한다. (t2=t가 0이 아니기 때문에 가능)
- 우측 하단의 식은 위와 동일하지만, b틸다가 아닌 b가 사용된 것을 알 수 있고, 이로 인해서 부등호가 적용된다.

Rate stability는 다음과 같은 상황을 지칭한다.

→ 앞서 본 식에서 limit을 취했을 때를 가정한 것이다.
→ 위 식을 해석해보자면, 시간이 계속해서 흐를수록 쌓이는 양이 없이 처리를 잘 한다는 뜻이다.(큐가 수렴한다는 뜻이다.)
저걸 만족하려면 어떻게 해야될까? 다음을 먼저 정의해보자.
1. 들어오는 일의 양의 수렴 값 → a
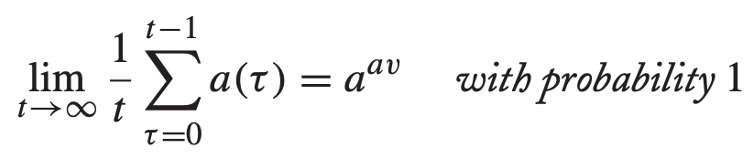
2. 처리될 수 있는 일의 양의 수렴 값 → b
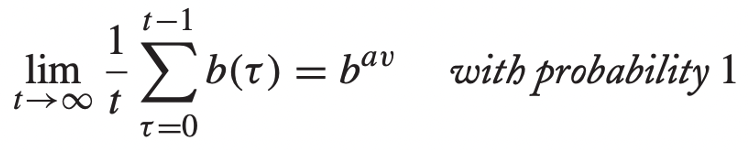
3. 편의 상 각각을 a와 b로 notation을 정의하겠다.
그럼, a <= b를 만족하기만 한다면 시간이 계속 지났을 때 큐는 0으로 수렴하게 될 것이다!
→ a > b 라고 한다면, a - b로 큐가 수렴되게 될 것이다.

야무진 예제를 살펴보자.
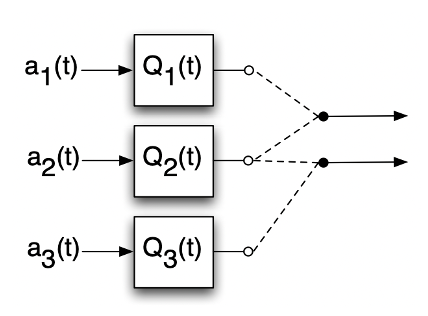
1. 모든 패킷은 고정된 길이를 갖고 각 Queue에 입력으로 들어온다.
2. 라우터에 할당된 Queue는 한 슬롯에서 하나의 패킷만을 처리할 수 있다.
3. 매 슬롯에서, 우리는 어떤 Queue로 서비스 해야할지 골라야 한다. (한 슬롯에서 2개씩)
Q. Design a router allocation algorithm to make all queues to be rate stable when arrical rates are given as follows.
자 그러면 as follows를 보자!
→ 여기서 사용되는 a는 각 Queue로 유입의 수렴 값(a^av)을 의미한다.
처리량(b(t))는 다음과 같이 정의된다.

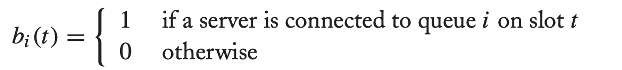
→ 단순히 위 조건 중 (2)번을 의미한다.

각 큐가 선택된 확률이 (0.5, 0.5, 0.9)라고 이해해도 괜찮다.
→ Law of large number 때문이고, 각 큐로의 유입이 1이라고 해석해도 괜찮기 때문이다.
그러면 큐가 서비스할 확률을 한 번 살펴보자. (문제에서 정의해준다.)
1. 0.5의 확률로 (0, 1, 1)
2. 0.5의 확률로 (1, 0, 1)
위의 확률이 주어졌을 때, Law of large number에 따라 b1, b2, b3가 어떻게 수렴될지 생각해보자.
1. b1 : 두 개의 choice에서 0.5의 확률만을 가지니, b1 = 0.5
2. b2 : 두 개의 choice에서 0.5의 확률만을 가지니, b2 = 0.5
3. b3 : 두 개의 choice에서 모두 있으니, b3 = 1
자, 수렴 값을 모두 찾았으니 이제 rate stable한지 확인을 해보면,

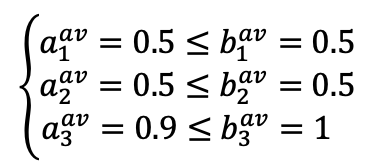
→ 모두 만족하는 것을 알 수 있다!
→ 따라서, 위와 같이 확률적 모델링을 한 네트워크 환경은 rate stable하다.

또 야무진 예제를 하나 보자.
1. a1과 a2는 매 timeslot에서 유입되는 패킷의 양이다. i.i.d.이고, 각각의 expectation은
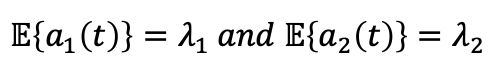
2. S는 channel state vector로서, network controller가 매 timeslot의 시작 부분에서 확인하는 값이다.
  
  → 네 개의 경우의 수가 존재하고, 채널이 모두 ON일 때 어떤 채널을 선택해야할지 골라야한다.
먼저, 각 lambda 값에 대한 boundary는 다음과 같이 정의될 수 있다.
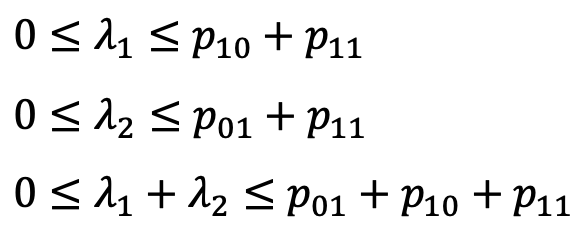
이를 만족할 수 있는 여러 lambda 값이 존재할 수 있고, 앞서 정의된 p_xx의 확률 값을 (0.24, 0.36, 0.16, 0.24)로 가정한다면

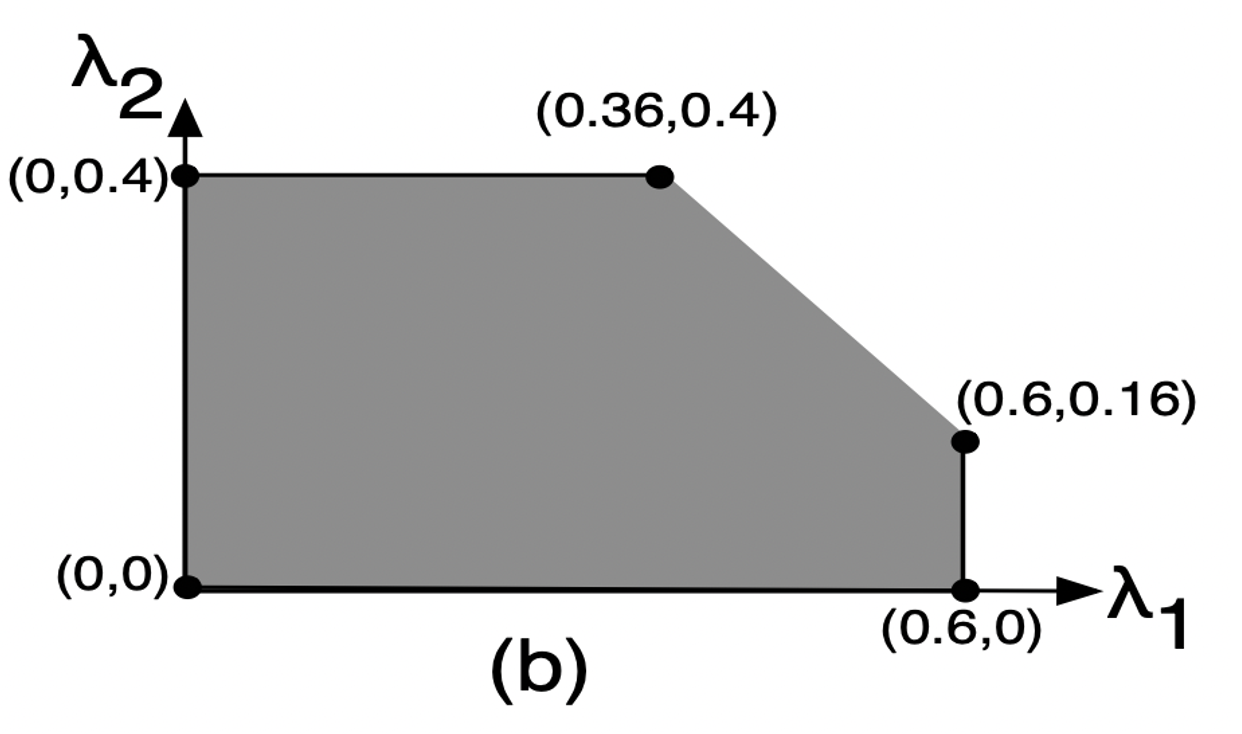
→ 가능한 lambda의 영역은 위 그래프와 같이 만들어질 수 있다. 이를 Network capacity region이라고 한다.
Q. 만약 LAMBDA=(0.5, 0.26)이라고 한다면, 1번 채널이 선택될 확률이 몇이 되어야 할까?

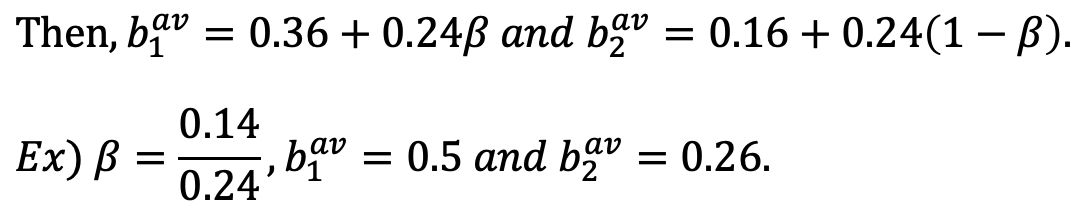
→ 여러 beta 값이 rate stability를 만족시키면서 선택될 수 있겠지만, 예시로 0.14/0.24도 설정될 수 있다.