Conditioning and Independence

Conditioning and Independence

현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.

Conditional Probability

• How should I change my belief about event A, if I come to know that event B occurs?

• Notation : P( A | B ) → probability of A, given B occurs.

• P( - | B ) : probability of something, given B occurs. → 이것도 하나의 probability law이기 때문에, 3 axioms를 만족시켜야 함

• P(A | B)를 어떻게 정의해야 할까?

  1. P( - | B ) = P(- ∩ B) 이걸로 해보자!

     • probability of A given B는 both A and B occur이니까.

     • 하지만 이것은 틀린 가정! → 3 axioms를 모두 만족하지 않음

       → P( Ω | B ) = P(Ω ∩ B) = P(B) != 1

  2. Normalization을 적용해서 P( - | B ) = P(- ∩ B) / P(B), P(B) > 0 으로 해보자.

     • 3 axioms를 만족하는가?
       1. Nonnegativity : good
       2. Finite additivity and countable additivity, For any two disjoint A and C
          • P( A U C | B ) = P[( A U C ) ∩ B] / P(B) = P[(A ∩ B) U (C ∩ B)] / P(B) = P( A | B ) + P( C | B) → P(A ∩ B)와 P(C ∩ B) 또한 disjoint → Finite는 countable로 확장할 수 있으니 생략
       3. Normalization : P( Ω | B ) = P(Ω ∩ B) / P(B) = P(B) / P(B) = 1
          

Bayes’ Rule and Bayesian Inference

• Porbability of A given that B occurs VS Probability of B given that A occurs

• Bayes’ Rule은 ‘추론(inference)’을 만들기 위해 사용된다.

• 이게 무슨 말일까?

  • 아래와 같이 이벤트가 있다고 가정을 해보자.

  • A1 : Happy😃 , A2 : Sad😢 → Ai : state / cause / original value
  • B : Shout! → B : result / resulting action / noisy measurement
  • 그리고 나는 관찰이나 이전의 데이터를 통해 P(A1), P(A2), P(B|A1), P(B|A2)를 알고 있다.
  • 그렇다면 이 때, P(A1 | B)와 P(A2 | B)를 어떻게 알 수 있을까?? → 결과만을 봤을 때, 무엇이 이 결과를 만들었다고 생각할 수 있을까??? → What is the reason? == Inference!
    

• 이러한 일을 어떻게 하는지 알아보기 전에, 몇개의 수학적 룰을 확인해보자

  1. Multiplication Rule (MR) : 일련의 event 발생을 계산하기 위한 Rule
     • P(B | A) = P(A ∩ B) / P(A) → P(A ∩ B) = P(A)P(B | A) → P(A^c ∩ B ∩ C^c) = P(A^c ∩ B) * P(C^c | A^c ∩ B) (* : dot product) = P(A^c) * P(B | A^c) * P(C^c | A^c ∩ B)
     • 이걸 시각화해서 이해를 해보자 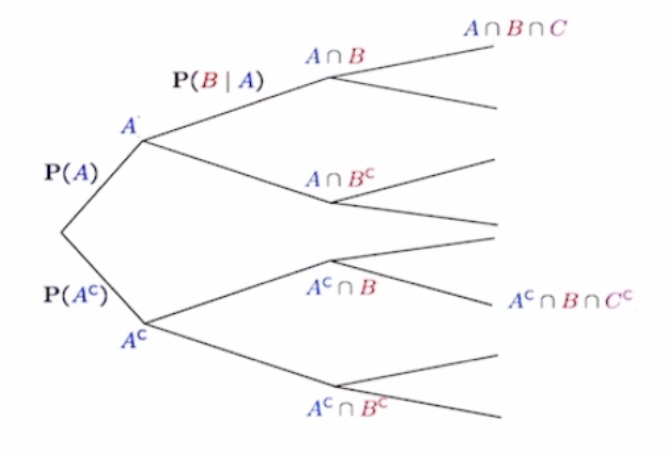→ 첫 두 간선은 A가 발생할 확률, A가 발생하지 않을 확률을 의미하고, → 다음 간선은, A의 발생 여부 이후 B가 발생했는지 않했는지를 확인한다….. → Multiplication Rule은 일련의 event와 관계되어 있으므로 A가 발생하고 B가 발생할 확률은 P(A)*P(B | A)이고 이는 P(A ∩ B)로 표현될 수 있다.
     • 일반화를 시켜보자
       • P(A1 ∩ A2 ∩ … ∩ An) = P(A1) * P(A2|A1) * P(A3|A1, A2) … *(An|A1, …, An)
         
  2. Total Probability Theorem (TPT)
     • Partition 개념을 사용하고, 이는 sample space(Ω)를 여러개로 나눈 것이다. → 나눠진 partition은 mutually exclusive해야 하고, Ω = A1 U A2 U A3 … 을 만족해야 한다.
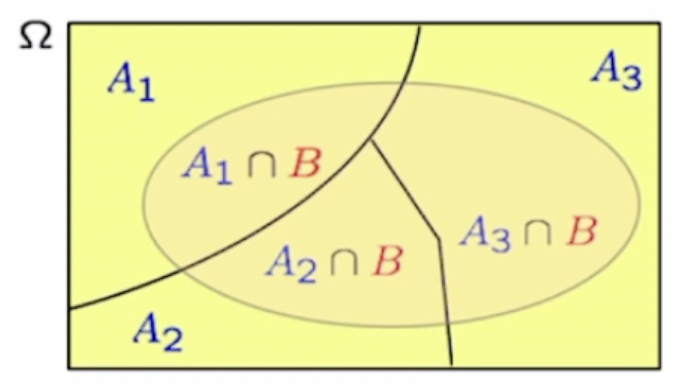
     • partition을 사용할 때, P(Ai) 그리고 P(B | Ai)를 안다면 P(B)를 알 수 있다. → P(B) = ΣP(Ai)P(B | Ai) → 어디서 본 듯한 형태지 않은가? → [결과]에 [가중치]를 곱한 형태이다. → 결과만 봤을 때, 이유를 알 수 있을 것만 같다!!
       

• 자, 이제 이것을 적용해서 Bayes’ Rule을 설명해보자.

  • 앞서 말한 것 처럼 Bayes’ Rule은 추론을 만드는 방법이고, 추론은 결과를 보고 무엇이 이 결과를 만들었는지를 찾아내는 방법이다.

  • 우리는 sample space를 partition한 A1, A2, A3를 알고 있고, P(Ai)와 P(B | Ai)를 추가적으로 알고 있다.

  • 추론은 여기서 P(Ai | B)를 알고 싶은 것이므로,

    1. MR을 사용해서, → P(Ai | B) = P(Ai ∩ B) / P(B)임을 알 수 있고
    2. MR과 TPT을 사용해서, → P(Ai | B) = { P(Ai)P(B | Ai) } / { Σj P(Aj)P(B | Aj) } 임을 알 수 있게 된다!!

    
    

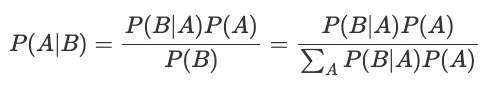
• 응용해서, 앞선 예제를 풀어보자!

  A1 : Happy😃 , A2 : Sad😢 → Ai : state / cause / original value

  B : Shout! → B : result / resulting action Assume : P(A1) = 0.7 , P(A2) = 0.3, P(B | A1) = 0.3 , P(B | A2) = 0.5

  • Calculate P(A1 | B) and P(A2 | B)

    • P(A1)P(B | A1) = 0.7 * 0.3 = 0.21 = P(A1 ∩ B)
    • P(A2)P(B | A2) = 0.3 * 0.5 = 0.15 = P(A2 ∩ B) = P(A1^c ∩ B)
    • P(B) = 0.21 + 0.15 = 0.36 = P(A1 ∩ B) + P(A1^c ∩ B)
    1. P(A1 | B) = P(B | A1)P(A1) / P(B) = 0.21 / 0.36 = 0.583
    2. P(A2 | B) + P(B | A2)P(A2) / P(B) = 0.15 / 0.36 = 0.417

  • 짜잔🕺 신기하다 근데 왜 P(B) = P(A1 ∩ B) + P(A1^c ∩ B)가 성립하는지 모르겠다!
    

Independence, Conditional Independence

• Can I ignore my knowledge about event B, when I consider event A?

• Independence가 왜 필요할까?

  • 가정을 해보자.
    1. Event A : I get the grade A in the probability class. (my interest)
    2. Event B : My friend is rich
  • 명백하게(아닐 수도 있지만), A와 B는 연관이 없고, my interest를 위해 B를 사용하지 않아도 된다. → Independence makes our analysis and modeling much simpler!

• Definition : Occurence of A provides no new information about B. Thus, knowledge about A does NOT change my belief about B. → P(B | A) = P(B) = P(A ∩ B) / P(A) → P(A ∩ B) = P(A) X P(B) → P ㅛ B (typora가 저런 기호를 어디서 가져오는지 모르겠다. 눈치 못챘으면 됐다.)

  1. 그러면, A and B disjoint가 A ㅛ B일까?? → 전혀 그렇지 않다. A와 B는 really dependent관계이다. → A가 발생 했을 때, B가 발생하지 않음을 알고 있기 때문이다.
  2. 그러면, A ㅛ B일 때, A ㅛ B^c일까?? → 그렇다. A와 B가 independence라면 A와 B^c 또한 independence이다.
     

• Conditional Independence

  • Conditional probability에서 말했 듯이 P(-)도 probability law이고, P(-|C) 또한 probability law이다. 그러면 여기에도 independence가 적용될 수 있다!
  • Event A, B, C가 있고, A와 B가 independence하다면, → P(B | A ∩ C) = P(B | C) 라고 표현할 수 있다. → A ㅛ B|C → P(A ∩ B | C) = P(A | C) X P(B | C) 이다.
  • 증명은 다음과 같다.
    1. P(A ∩ B | C) = { P[B ∩ (A ∩ C)] } / P(C) = { P(A ∩ C)P(B | A ∩ C) }/ P(C) = P(A | C) X P(B | C)
       

• A ㅛ B와 A ㅛ B|C의 차이점은 무엇일까?

  • 먼저, 이 예시를 생각해보자

    Suppose that A and B are independent. If you heard that C occured, A and B are still independent?

    → 일단 난 그렇다고 생각했다. 당연히 내가 틀렸다.

  • 간단한 예시를 통한 설명을 보자면,

    Two independent coin tosses,

    ​ H1 : 1st toss is a head.

    ​ H2 : 2nd toss is a head. ​ D : two tosses have different results.

    → H1과 H2는 independent하다는 것은 당연하다. → P(H1 | D) = 1/2 , P(H2 | D) = 1/2 인 것도 구해질 수 있다. → 내 생각이 맞다면! P(H1 ∩ H2 | D) = P(H1 | D) X P(H2 | D) = 1/4가 되어야 한다. → 하지만 두 동전이 Head인데 다른 결과라고 볼 수 없다. 즉, 0이 나와야 한다. → 즉, C가 발생했다고 해서 A와 B가 여전히 independent하다고 할 수 없다.
    

• 그러면, A ㅛ B|C일 때, A ㅛ B가 성립을 할까? → 결과적으로는 그렇지 않다. 예시를 통해 설명해 보겠다.

  두 개의 동전이 있다. 각각은 Blue(B)와 Red(A)이고, 두 개 중 하나를 uniformly하게 선택한다.

  그런 다음 선택한 동전을 두 번 independent하게 던진다. Assume )

  ​ P(Head of Blue) = 0.9 and P(Head of Red) = 0.1

  ​ Hi : i-th toss is head, B : Blue is selected(0.5).

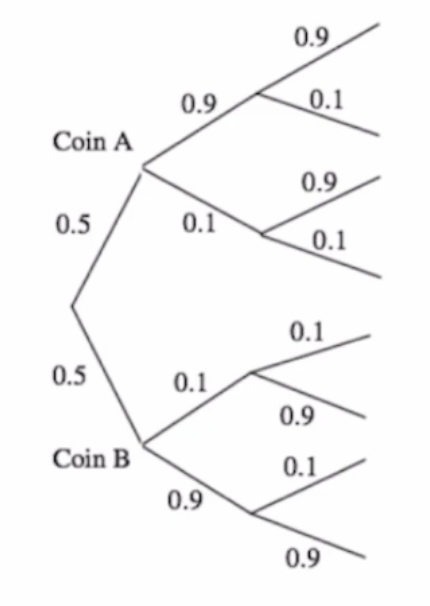
  • 여기서, H1 ㅛ H2|B는 성립한다. independent하게 던지니까. 수식으로 보자. → P(H1 ∩ H2 | B) = 0.9 X 0.9 = P(H1 | B) X P(H2 | B) = 0.9 X 0.9
  • 그럼… H1 ㅛ H2도 성립을 할까? 그렇지 않다. 먼저, P(H1) = P(B)P(H1 | B) + P(B^c)P(H1 | B^c) = (0.9 / 2) + (0.1 / 2) = 1/2 그러면, 동전을 던졌을 때 앞뒤가 나오는 확률은 변하지 않으니까 P(H2) = P(H1)이 나와야 한다. H1 ㅛ H2라면, P(H1 ∩ H2) = P(H1) X P(H2) = 1/4가 나와야 한다. → P(H1 ∩ H2) = P(B)P(H1 ∩ H2 | B) + P(B^c)P(H1 ∩ H2 | B^c) = (0.9 * 0.9)/2 + (0.1 * 0.1)/2 != 1/4 이기 때문에 H1 ㅛ H2는 성립하지 않는다.
    

• Independence of Multiple Events

  • 지금까지는 두 개의 events가 independent한 condition을 확인해봤다.

  • 그럼 여러 개일 경우에는 어떻게 해야할까?

    이렇게 하면 된다~