Probabilistic Model

1. Probabilistic Model

현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.

Probabilistic Model

Mathematical description of uncertain situations

• Modeling : Understand reality with a simple mathematical model
  • Experiment : flip two coins → can observe a random outcome.
    • All outcomes : {(H, H), (H, T), (T, H), (T, T)}
  • 이러한 가정에서 우리가 해야할 일은 실험을 통해 얻어진 random outcomes를 기반으로 probabilistic model을 만드는 것
• Probabilistic model이란?
  • 모델을 만들기 위해서, set of outcomes에게 ‘번호’를 부여 → 이러한 ‘번호’는 how probable some outcome is going to occur을 의미
  • 이렇게 만들어진 모델은 uncertain situation을 수학적으로 설명할 수 있음
  • 모델은 core elements 로 구성되어 있음
• 오늘은 probabilistic model을 위한 sample space와 probability law를 수학적으로 정립되도록 설정하는 방법을 정리해 보겠습니다.

Sample Space, Event, Probability Law

Elements of probability theory

• Sample Space? → The set of all outcomes of MY INTEREST

  • Condition of Sample Space

    1) Mutually exclusive → 어떤 사건이 발생하게 되면 다른 이벤트는 발생하지 않는다.

    Sample Space	Elements	Mutually exclusive?
    Toss a Coin	{H, T, HT}	X
    Toss a Coin	{H, T}	O

    → 동전 던지기는 앞면 or 뒷면만이 존재할 수 있음 (Not H and T)

    2) Collectively exhaustive → Sample space는 모든 상황을 커버할 수 있어야 함 → 발생할 수 없는 일이 sample space에 존재해서는 안 됨

    Sample Space	Elements	Collectively exhaustive?
    Toss a Coin	{H}	X
    Toss a Coin	{H, T}	O

    → {H}는 T라는 발생할 수 있는 상황을 포함하고 있지 않음

    3) At the RIGHT GRANULARITY, Not too concrete, not too abstract

    • 내 interest가 동전의 앞, 뒷면 결과에 따른 날씨의 영향이라고 해보자.

      Sample Space	Right granularity?
      {H, T}	X (too abstract)
      {(H, R), (T, R), (H, NR), (T, NR)}	O

      → R(Rain), NR(No Rain) → 마지막 sample space와 같이 내 interest에 부합하도록 ‘날씨’와 ‘동전’의 연관성(and)을 생각해서 sample space를 구성해야 함

  • Sample space의 종류

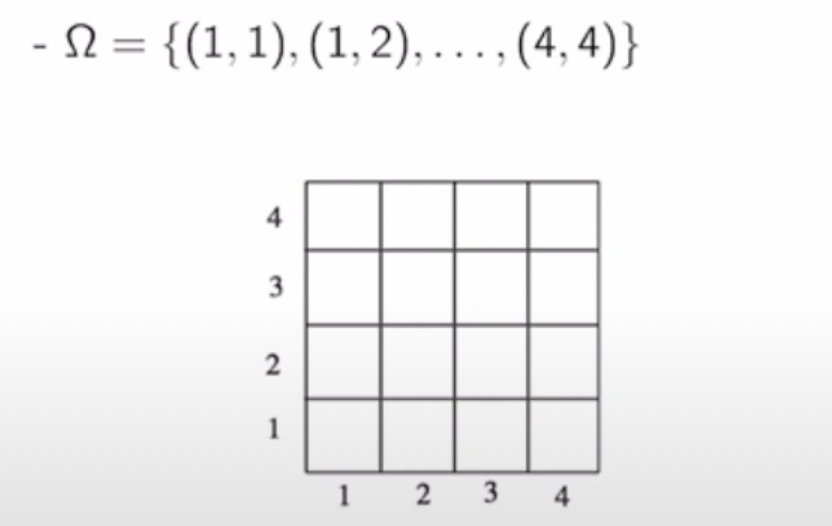
    1. Discrete case : Two rolls of a tetrahedral die
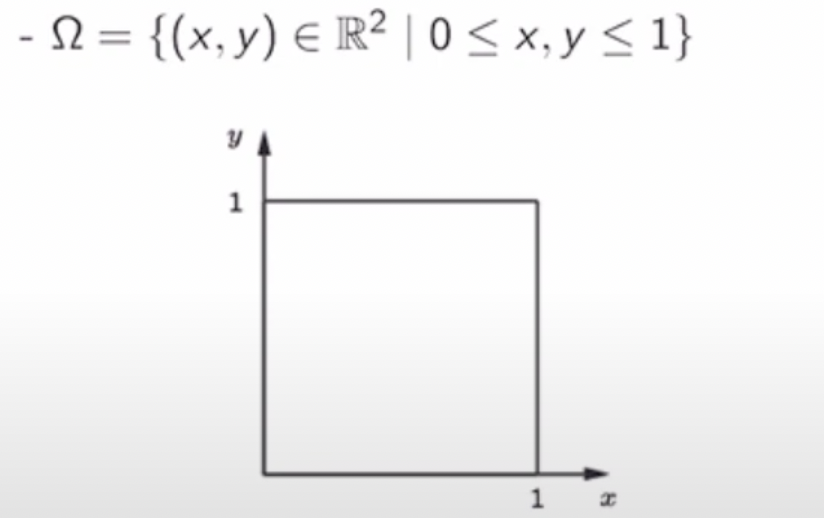
    2. Continuous case : Dropping a needle in a plain

  • Probability Law : Decide “Assign numbers to what?”

    • Continuous case에서 정확히 좌표상 (0.5, 0.5)에 바늘을 떨어뜨릴 확률은? → 0이다. 좌표는 무수히 많기 때문. → 그렇다면, 이러한 경우엔 each outcome에 대한 number를 할당할 수 없음 → subset of Ω에 number를 할당 → subset of Ω == an event
    • P(A) (Probability Law) = Probability of an event A → 주사위를 굴릴 때, 홀수일 확률은? → Ω = {1, 2, …, 6} → A = {1, 3, 5} (이벤트를 가정, 하지만 A ⊂ Ω을 만족해야 함)

Probability Axioms

3 axioms for the completeness of a theory

• What is the starting points to construct P(-) that naturally satisfies the intention of a probability theory designer?

  1. P(A) >= 0 for any event A ⊂ Ω (Nonnegativity)

  2. P(A ∪ B) = P(A) + P(B) - P(A ∩ B)

  3. P(A ∪ B) <= P(A) + P(B) → For two disjoint events A and B, P(A ∪ B) = P(A) + P(B) (Finite additivity)

     → 확장해보면, For any finite number of disjoint events,

     ​ A1, A2, …, An에 대해서, P(A1 ∪ A2 ∪ … ∪ An) = P(A1) + P(A2) + … + P(An)

     → Disjoint : P(A ∩ B) = 0

  4. P(Ω) = 1 (Normalization)

  5. P(Ø) = 0

  6. many others…

• 꼭 그리고 이것만 지키면 된다! → No other things are necessary, and we can prove all other things from the above axioms.

  1. Nonnegativity

  2. Normalization

  3. Finite additivity

• Examples)

  1. For any event A, P(A) <= 1 을 기반으로 3 axioms를 발견
     • 1 = P(Ω) = P (A U A^c) : Normalization
     • P (A U A^c) = P(A) + P(A^c) : Finite additivity
     • P(A) = 1 - P(A^c) <= 1 → P(A^c) >= 0 (A^c is also any event)

• Probability Calculation Steps

  1. Specify the sample space
  2. Specify a probability law → from my earlier belief, from data, from expert’s opinion…
  3. Identify an event of interest
  4. Calculate

• Examples)

  • Toss a coin (Biased)

    1. Ω = {H, T}
    2. P({H}) = 1/4, P({T}) = 3/4
    3. I want to know Probabilty of head or tail
    4. 1/4, 3/4

  • Discrete but infinite sample space

    • Ω = {1, 2, 3, …}, P({n}) = 1/(2^n), n = 1, 2, …

    • Is the above Probability law legitimate? → seems OK! → P(Ω) = 1/2 + 1/(2^2) + … = (1/2) / (1- 1/2) = 1

    • I want to know P(even numbers) !!! → P(even) = P({2, 4, 6, …}) = 1/(2^2) + 1/(2^4) + … = 1/3

    • Hmm… Is the above right? if not, why? → Wrong, FINITE ADDITIVITY axiom does not allow this. → 이해가 잘 가지 않는 부분…(08:04 ~ 10:42)

    • So, we have to change FINNITE to COUNTABLE

      1. Nonnegativity
      2. Normalization
      3. Countable additivity (finite ⊂ countable) → For any infinite number of disjoint events, A1, A2, A3, …에 대해서, P(A1 ∪ A2 ∪ A3 ∪ …) = P(A1) + P(A2) + P(A3) + …

      ** 그래서 이게 성립된다는거야 만다는거야….