Random Processes (1)

Random Processes (1)

현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.

• 드디어 새로운 목차다.
• Random Process는 머신러닝, 통신 시스템 등에서 아주아주 많이 쓰이는 개념이라고 한다.

Introduction of Random Processes

• Many probabilistic experiments that evolve in time
  • Sequence of daily prices of a stock
  • Sequence of scores in football
  • Sequence failure times of a machine
  • Sequence of traffic loads in Internet
• Random Processes는 이러한 것에 대한 수학적 모델을 만들기 위해 존재한다.

Random Process : Basic (1)

• 랜덤 프로세스의 정의는 다음과 같다.
  → A random process is a sequence of Random Variables indexed by time.
• 여기서 시간은 모델링 방법에 따라 discrete or continuous일 수 있다.
• Notation
  
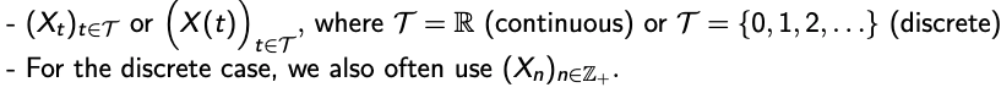
• 어떤 특정한 시간에 대해서, t, Xt, X(t)는 RV이다.
  • 여기서, t, Xt, X(t)는 discrete or continous이다.

Random Process : Basic (2)

• Discrete case 와 Continous case에 대한 예제를 한 번 보자.
  

  1. Discrete

  
  

  → Xi는 i 시간에 해당하는 RV이다. 따라서, Xi는 sample space의 값을 실수로 mapping하는 역할을 한다. 그것이 w
  → 마지막에서, X3(w1)은 X에서 3번째 고정된 시간에 w1에 대한 아웃풋의 값이므로 130이 된다.
  
  

  2. Continuous

  
  → Discrete와 매우 유사하다.
  → 하지만 Notation을 사용하는 방법이 있음을 확인하자.
  
  

  	Discrete	Continuous
  Notation	Xt(w)	X(t, w)

  
  

Random Processes: Our Interest

• 근데, 우리는 CLT, WLLN에서 a sequence (or a collection) of RVs에 대해 배웠다.
• 도대체 무엇이 다를까?
• 간단하게 생각하기 위해 discrete한 경우를 생각해보자.

1. Physical difference
   1. RP는 infinite sequence of RVs(X1, X2, …)를 다룬다.
   2. 즉, outcome은 a infinite sequence of sample values x1, x2, …이다.
2. Semantic difference
   1. Dependence : 현재 시간과 다른 시간 또는 어떤 시간과 또 다른 시간에서의 Xi들의 연관성을 알 수 있다.
   2. Long-term behavior : 향후 발생할 미래에 대한 예측이 가능하다.
      → What is the fraction of times that a stock price is above 3000?
      

4 Types of Random Processes

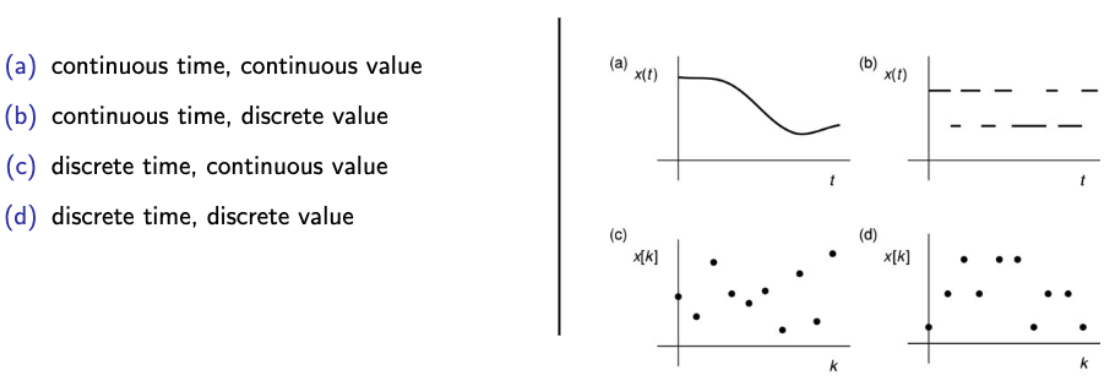
→ 우리가 무엇을 원하냐에 따라 4가지 중 어떤 것을 사용해도 된다.
→ (a) : 모든 시간대에서 변동하는 비트코인의 가격

Random Processes in This Course

• 간단하게 무엇을 배우는가에 대해서 알아보자.

Bernoulli	Poisson	Markov
Discrete Time Xi ㅛ Xi-1, Xi-2, … 오늘은 과거와 관련이 없다!	Continuous time version of BP s~t 기간의 일과 t~t+a 사이의 일은 관련 없다! 오늘은 과거와 관련이 없다와 비슷!	Discrete Time One-step more general than BP/PP 오늘은 ‘어제’와만 관련이 있고, 그 나머지는 관련이 없다!

Bernoulli Process

• 가장 간단한 Random Process의 한 형태이다.

Bernoulli Process

• 간단한 예제를 하나 들어보자.
• At each minute, We toss a coin with probability of head 0 < p < 1.
  → 여기서 중요한 것은, 시간이 아닌 (물론 이것도 중요) 각 이벤트들이 independent하다는 것이다.
• 이러한 값들은 그러면 X1, X2, X3,…로 표현될 수 있고, 이것들은 Independent Bernoulli trials이다.
  → 여기에 야무지게 시간으로 indexing을 해주면 된다.
• BP는 discrete time과 discrete value를 위한 것이다.
• 또한, BP를 a type of ‘arrival’ process라고도 한다.
  → 서버로 데이터가 전송될 RP or 상점에 방문객이 존재할 RP

Number of arrivals and Time until the first arrival

• T라는 값이 # of slots until the first arrival이라고 해보자.
• 그러면 T는 RV를 의미하게 되고, 만약 (X, X, X, X, X, O)라고 하면 T는 6이라는 값을 가질 것이다.
• 이러한 T는 또한 Geometric Random variable이다.
  
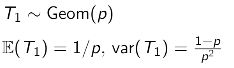
• Geom RV는 memoryless라는 속성도 갖고 있다.

Memoryless and Fresh-start after Deterministic time n

• 앞선 예제를 한(세) 마디로 표현하면 다음과 같다.
  → Independence across slots
• 어? 그럼 어떤 프로세스가 진행되다가 그 중간에 들여다보면 어떻게 보일까?
• 이것에 대한 질문을 여러가지 해보자.
  1. U = X1 + X2 ㅛ V = X5 + X6?
     → 매우 직관적으로 그렇다고 할 수 있다.
     → Because Xi s are independent.
     
  2. After time n = 6, I start to look at the process Xn (n=6 ~ INF)
     → (X1, X2, … , X5) ㅛ (X6, … XINF)
     → 즉, 우리는 이전 것과 상관없이 ‘우리의 입장’에서는 fresh-start와 같이 보일 것이다.
     → If you watch the on-going Bern process(p) from some time n, you still see the same Bern process(p).
     
     

Fresh-start after Random time N

• 더 빡센 질문이다.
• 우리가 언제 들여다 봐도 동일한 Bern process(p)를 볼 수 있다는 것은 위에서 알 수 있었다.
• 근데,,,,,,,시간이 random이라면?? 즉, ‘언제 들여다 본다’ 자체가 random variable이라면 어찌될까
• 예제를 통해 어떤 의문인가를 확인해보자.
  
  → 누군가가 process를 지켜보다 조건이 충족되었을 때, 나를 불러 확인하도록 하는 예제이다.
  1. Time of 3rd arrival에 해당하는 N은 7, 그 이후는 Bern process이다.
     → 이전에 3개가 도착한 것은 이미 확정되어 있다.
  2. (1)과 동일하다.
  3. 이건 어렵다…….. 결론을 말하자면 일단 답할 수 없고, n에서 본 순간 ‘111’이 나와야 하므로 ‘111’자체는 random이 될 수 없다.
     → 즉, 111이 나왔다 해도 n 이후의 process는 Bern process가 아니다.
     → 추가로, 이를 알기 위해 future knowledge가 필요하다.
     
     

Stopping time

• Stopping time이라는 말의 정의를 앞서 설명한 예제를 통해 설명할 수 있다.
• In probability theory, a random time N is said to be a stopping time, if the question of “N=n?” can be answered only from the present and the past knowledge of X1, X2, … Xn.
• 따라서, N 이후에 fresh-start라면, N은 stopping time이라고 할 수 있다.
• 앞선 예제에서, E1과 E2는 stopping time이다.

Distribution of Busy Periods (1)

• 예제를 하나 생각해보자.
• 어떤 서버가 있고, 요청이 들어왔을 때 busy(B), 아닐 때를 idle(I)라고 해보자.
• 여기서, First busy period B1을 다음과 같이 정의해보자.
  → Starts with the first busy slot and ends just before the first subsequent idle slot
• 무수히 많은 B1들이 있을텐데 두 개를 대표적으로 확인해보자.
  
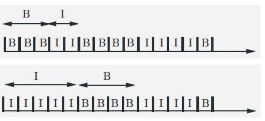
  1. B1 = 3
  2. B2 = 4
• 이런식으로 확인을 할 수 있고, 일반화해서 생각해본다면,
  1. Busy Period가 바로 시작
  2. Idle이 지속되다가 Busy Period가 시작
• 첫번째는 우리가 어디서 많이 본 RV로 치환할 수 있다.
  → Geometric Random Variable
• 두번째는? Fresh-start를 생각하자!
  → N이라는 새로운 RV가 time of the first busy slot이라고 한다면, N은 stopping time이다.
  → 왜냐? N 이후에는 Bern process를 fresh-start할 수 있기 때문이다!
  → 그러면, 그 이후는 Geometric Random Variable이다.
• 따라서, B1 is geometric with parameter (1-p)
  → p : idle

Distribution of Busy Periods (2)

• (1)과 똑같다. 하지만 두 번째 periods를 알고 싶다!!! (B2)
• 여기서 fresh-start의 힘을 알 수 있다.
  → N : time of the first busy slot of the second busy period
  → then, Is N a stopping time? → YES!
• 그럼 B2 are identically distributed as Geom(1-p).
• 이는 B3, B4,…에도 동일하게 적용할 수 있다.
  → 이것이 fresh-start의 힘이다.
  

Time of k-th arrival

• 이제 더 확장해서 생각해보자.
• Time of the first arrival을 Y1이라 하면, Y1 ~ Geom(p)일 것이다.
• 그러면!! Time of the k-th arrival은 어떻게 될까? 즉, Yk는 어떻게 될까?
• 먼저, 두 Yi, Yi+1의 interval time을 구하고 이 모든 것을 합하면 결국 Yk가 나올 것이다.
  → 이렇게 한 이유는, Yi는 i번째에서 봤을 때 fresh-time이고 i+1도 동일하기 때문이다.
  
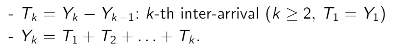
• 즉, After each Tk, the fresh-start occurs
  → Ti are i.i.d and ~Geom(p)
• i.i.d이기 때문에 다음도 도출할 수 있다.
  
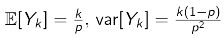
• 근데 아직 distribution을 구하지는 않았다.

PMF of Yk

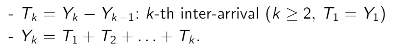
• Ti는 또한 i.i.d 이고 Geom(p)이다.
• 이제 PMF를 구해보자.
  
  → k번째 도착했을 때의 시간이 t일 경우는 다음과 같이 계산이 된다.
  → 먼저, 시간 t에서 arrival이 있으면서(and) k-1번의 arrivals가 t-1동안 있어야 한다.
  → Fresh-start!! 둘은 독립이다!!
  
  

Pascal Random Variable with Parameter (k, p)

• 바로 앞 예제인 PMF of Yk에서 배운 방법이 pascal rv에 대한 내용이다.
• 정의하자면 다음과 같다.
  → In the sequence of Bernoulli trials, the time Yk of k-th success.
• 식은 다음과 같다. parameter는 k와 p를 사용한다.
  
• Pascal(1, p) = Geom(p)
  → 당연히, 첫번째에 대한 것은 Geom이다.