Random Processes (3)
Random Processes (3)
현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.
Playing with Bern. and Poisson Process
Description via Inter-arrival Times
- 지금까지 배웠던 Bern.과 Poisson에서 Inter-arrival이라는 조건 하에서 생각해보자.
- Bern.과 Poisson의 간략하고 직관적인 설명을 확인해보자.

- 이번 정리에서부터 쭉 쓰게될 Notation은 다음과 같다.

Example.
- It has been observed that after a rainy day, the number of days until the next rain is Geom(p), indepedent of the past.
- Question. What is the probability that it rains on both the 5th and the 8th day of the month?
- 우리가 지금까지 배웠던 the geometric PMF를 사용한다면? 때에 따라 다소 어렵고 복잡한 문제가 될 수도 있다.
- 그래서 쉽게 생각해보자.
- Rainy days is a Bern. process
- Each rainy day is independent with probability p.
- 그럼 결론은? p^2이 된다. 쉽다!
Split: Bern. Process
- BP(p)를 두 개의 process로 나눠보자.
- 쉽게 생각해서, q라는 성공 확률을 갖고 성공 시 A 프로세스로 실패 시 B 프로세스로 옮긴다고 해보자. 그림은 다음과 같다.
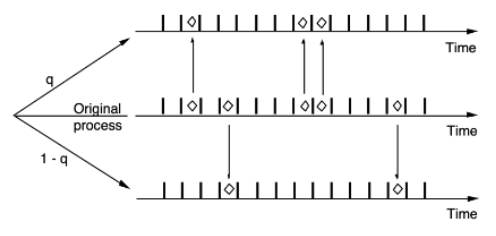
- Question. What are the two split processes?
→ BP(pq) and BP(p(1-q))
→ 새로운 BP가 두 개 생기게 된다! - 그럼, 이 두 BP가 서로 독립일까?
→ 당연히 아니다.
→ 하지만 각 프로세스의 각 슬롯끼리는 independent하다.
Merge: Bern. Process
- 자 이제 두 개를 합치는 상황에서는 어떻게 되는지 살펴보자.
- 이전과는 관계가 없는 문제라고 생각하고, Proc. 1과 Proc. 2를 합친다고 생각하자.
→ Merge BP(p) and BP(q) into one process.
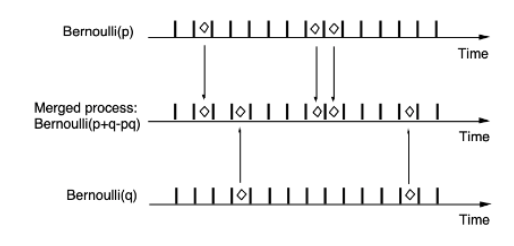
- 여기서, 1과 2의 특정 슬롯을 합칠 때 충돌이 발생한다면 merged process에는 하나만 들어간다고 하자.
- Question. Probability of having at least one arrival
→ 1 - (1 - p)(1 - q) = p + q - pq
→ 적어도 하나라고 말하는 이유는 Collid arrival에 대한 예외를 처리했기 떄문이다. - 그러면, 합쳐진다는 것이 ‘도착’이라고 해석한다면
→ Merged Process : BP( p + q - pq ) - 살짝 꼬아서, Merged proc.에 도착이 생겼을 때, 그것이 1번 proc.으로 부터 왔을 확률은?

Split: Poisson Process
-
개념은 Bern. Process를 split했던 것과 같다.
-
p의 확률로 keep process로 분리, 1-p의 확률로 discard process로 분리한다고 해보자.
-
그럼 이렇게 분리된 split process는 무엇일까?
→ 얘네도 Poisson Process이다. -
그래서 이들도 어떠한 속성을 갖게 되는데
-
Independence : 다른 시간대에 존재하는 process는 서로 독립적이다.
-
Time-homogeneity : 동일한 길이의 시간대에서의 process는 동일하다.
-
Small interval probability over δ-interval
→ keep process의 관점에서 보도록 하자.- 한 슬롯(δ-interval)에서 도착이 1개일 경우 : p(λδ + o(δ))
- 한 슬롯에서 도착이 2개(이상)일 경우 : p(o(δ))
- 한 슬롯에서 도착이 0개일 경우 : 1 - p(λδ + o(δ) + o(δ))
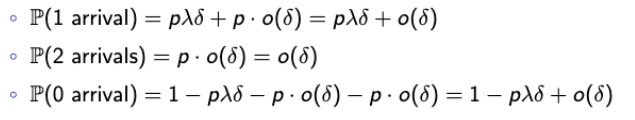
→ o(δ)는 negligible하다는 것을 기억하자.
-
-
따라서, 두 프로세스는 PP(λp)와 PP(λ(1-p))로 분리되게 된다.
Merge: Poisson Process
-
요놈도 개념은 Bern. Process를 merge했던 것과 같다.
-
PP(λ1)과 PP(λ2)를 Merge!
-
얘도 당연히 merged된 것은 Independence와 Time-Homogeneity를 갖게 된다.
-
그럼, 중요한 Small interval probability를 살펴보자.
- 한 슬롯에 도착이 없을 때 : (1 - λ1δ)(1 - λ2δ)
- 한 슬롯에 도착이 하나 있을 때 : λ1δ(1 - λ2δ) + (1 - λ1δ)λ2δ
- 한 슬롯에 도착이 두개 있을 때 : λ1δ * λ2δ
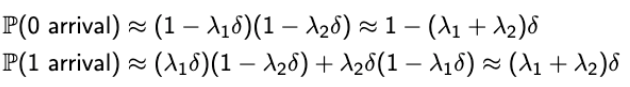
→ δ^2 은 negligible. -
따라서, Merged Process는 PP(λ1 + λ2)이다.
Cont.
- Merged에서 뭔가 더 생각해보자.
- Red : PP(λ1), Blue : PP(λ2)
- 그럼, Merged에 누군가 도착했는데, 얘가 Red에서 온 놈일 확률은 어떻게 될까?

→ 간단하게 구해질 수 있다. - 더 나아가서, 하나의 이벤트 Ak를 정의해보자.
→ Ak = {k-th arrival in the merged proc. is RED}- Ak의 확률은 당연히 앞서 구한 λ1/(λ1 + λ2)이다.
- 그리고, A1, A2, … Ak는 모두 독립적이다.
→ Red와 Blue가 독립이니까. - 그럼 10번의 도착 중에서 k개의 Red가 있을 확률은??
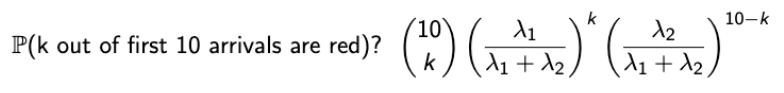
→ Binomial의 형태를 갖게 된다!
Using Poisson Processes for Intuitive Problem Solving
- 지금까지 배웠던 Split과 Merge가 실제 문제에서 어떻게 사용되는지 확인해보자.
Competing Exponential (1)
-
두 개의 독립적인 전구가 있다고 해보자. 그리고 이들의 생명을 Exponential RV로 모델링하자.

-
Question. Distibution of Z = min(Ta, Tb), the first time when a bulb burns out?
Approach 1.
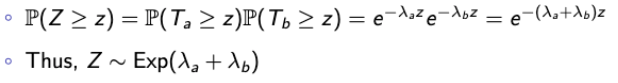
→ 근데 우리는 Poisson Process를 Merge하는 방법을 알고 있으니까, 그걸 적용해보자.
Approach 2.

→ 훨씬 간결하게 풀 수 있다. (확장된다면)
Competing Exponential (2)
- 그럼 확장해보자!
- 세 개의 전구가 있고 각각은 Exp(λ)로 생명이 모델링 되어 있다.
- Question. E[time until the last bulb burns out]
- 먼저, 세 개의 Merged Poisson Process를 생각해보자
- Time until the first burn-out : T1 = Exp(λ + λ + λ) = Exp(3λ)
- Time until the second burn-out : T2 = Exp(λ + λ) = Exp(2λ)
- Time until the third burn-out : T3 = Exp(λ)
- 이렇게 만들어버리면 E[time until the last bulb burns out] = E[ T1 + T2 + T3 ]가 된다.
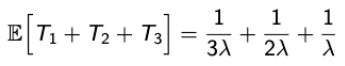
### Sum of Independent Poisson RVs
-
두 개의 독립적인 X와 Y RV가 있다고 해보자. 각각은 X ~ Poisson(μ)와 Y ~ Poisson(v).
-
Question. Distirution of X + Y?
→ RV의 덧셈은 Convolution을 사용하면 됐었는데, 이건 복잡하고 귀찮다.
→ 그러면, PP(λ) = # of arrivals in 𝛕(N𝛕) ~ Poisson(λ𝛕)라는 것을 기억해서 X 와 Y에서 PP를 추출하자. -
Poisson Process perspective.

→ 그럼 각각은 μ와 v를 시간으로 갖는 PP가 만들어질 것이고 X와 Y는 독립이였기 때문에 disjoint time interval을 갖게 된다.(일종의 연속된 시간으로도 볼 수 있다.) -
따라서, 질문에 대한 답은 μ와 v의 시간 동안의 # of arrivals of PP(1)이 되고, 따라서
→ X + Y ~ Poisson(μ + v)
Poisson arrivals during Exponential Interval (1)
- Random Time Interval 에서의 PP를 생각해보자.
- PP(λ)와 하나의 독립적인 RV T ~ Exp(v)로 생각해보자.
- Question. Distribution of N_T ?
- 우리가 배웠던 것 중에 Total Probability Theorem을 사용해서 생각해보자.
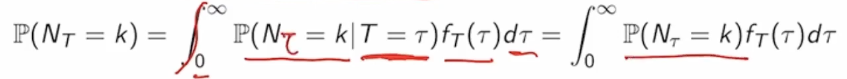
→ 흠,,, 근데 무지하게 복잡해보인다. - 그럼 ‘진짜’ 배웠던 것을 써보자!
Cont.
- 새로운 PP를 도입하자.
→ PP(v) - 머리속에서 PP(λ)와 PP(v)의 Merge에 대한 상상의 그림을 펼쳐보면,
- Merged Process에서 PP(λ)로 부터 도착들이 합쳐지다가
- 어느 순간 PP(v)에서 온 애가 등장할 것이다.
- 그럼, 이 순간 전까지의 PP(λ)를 구하면 된다.
- 구해보자.

→ ㅇㅋ - K라는 RV를 하나 생성하고 이 친구의 정의를 다음과 같이 내려보자
→ K : number of total arrivals until we get the first arrival from PP(v).
→ Then, K ~ Geom(v / (λ + v))
→ 즉, 성공 확률을 v / (λ + v)로 갖는 Geom RV가 된다. - 이렇게 만들어진 Geom RV의 문제점은 성공까지 횟수를 Count한다는 것이다.
→ 그럼 하나 빼자! - Let L be the number of arrivals from PP(λ) until we get the first arrival from PP(v).
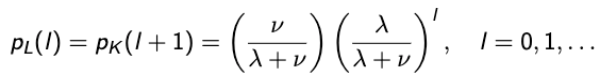
→ 5개의 도착이 있으려면, 6개의 시도 중 하나의 성공이 있으면 된다.
Approximation of Binomial : Poisson vs. Normal
- 우리가 배웠던 Central Limit Theorem에 따르면,
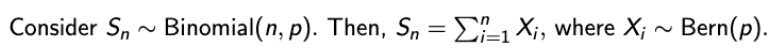
- n이 무한대로 갈 때를 상정했던 것이니까, Poisson RV도 여기에 숟가락을 얹을 수 있지 않을까?
- 일단 둘의 차이점을 살펴보자.
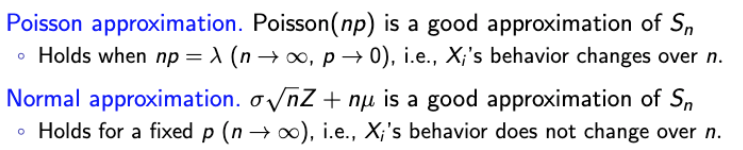
→ 가장 큰 차이점은 Poisson에서는 p도 변하는 값이라는 것이다.
→ 따라서, Xi도 이에 따라 영향을 받게 된다. - 그럼 언제는 Poisson을 써야하고, 언제는 Normal을 써야 할까?

→ 현장에서는 p와 n이 주어질 때가 많다고 한다. 따라서 어떤 방식을 쓸지 정하는 것이 중요하다.
Random Incidence Phenomenon
Example : Survey of Utilization of Town buses
- “도시의 버스 운용이 얼마나 잘 되고 있는가?”에 대한 설문 조사를 한다고 한다.
- 우리는 여기서 두 가지의 가정을 할 수 있다.
- (1) 랜덤으로 몇 개의 버스를 선택하고, (2)그 버스의 승객 수를 구한다.
- (1)버스 탑승객을 랜덤으로 선택하고, (2) 승객들이 탄 버스를 알아낸 다음에 (3) 그 버스의 이용자 수를 구한다.
- 그럼 이렇게 했을 때, [1]과 [2]의 가정을 통해 구해진 수가 다를까? 아님 차이가 날까?
→ Sampling method에 관련된 문제이다. - 이 이후에 나오는 내용은 이를 다루게 된다.
Random Incidence Phenomenon
-
하나의 예제를 들어보자.
-
고정된 시간 t에 나는 버스 정류장으로 간다.
*시간은 PP(λ), ~ Exp(λ)로 모델링- 정류장에 있는 사람에게 “이전 버스는 언제 왔나요?”라고 물어본다.
→ 답변은 U에 왔어요. - 그리고 기다렸다가 다음 버스가 왔을 때, 나는 시간을 측정한다.
→ 그 시간은 V이다.
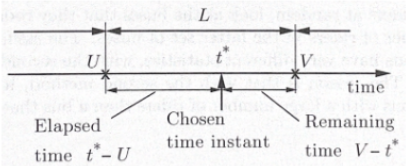
- 정류장에 있는 사람에게 “이전 버스는 언제 왔나요?”라고 물어본다.
-
U와 V 동안의 시간을 L이라고 했을 때, Distribution은 어떻게 구해야할까?
→ 당연히 Exp(λ)아닌교? -
아니다. 여기서 중요한 점은 t*는 고정된 시간이다. (그래서 incidence)
Distribution of L
-
우리는 t*이라는 Additional condition을 주었으니까, 일단은 L을 다음과 같이 표기한다.
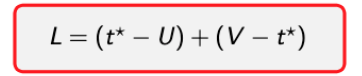
→ 이제 항별로 따져보자.-
V - t* : 내가가 좋아하는 memoryless 덕분에 fresh-start!
→ V - t* ~ Exp(λ) -
t* - U : 아~ 이게 애매하다. ‘이전’의 시간이다…
→ Trick을 사용하자. 시간을 거꾸로 본다면, 결국은 이후의 시간이 된다.수학적으로 이를 확인해보자면,
P(t* - U > x) = P(no arrivals over[ t* - x , t* ])
= e^(-λx) = P(T_inter > x)
→ Thus, t* - U ~ Exp(λ)
-
-
이걸 종합해보면, L = X1 + X2 이고 X1, X2 ~ Exp(λ)이다.
→ Time until we have two arrivals in PP(λ).
→ Erlang RV with parameter(2, λ)
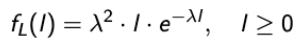
-
이는 Mean 값으로 2/λ를 갖게 되는데, Exp(λ)의 Mean이 1/λ라는 것을 생각하면 평균보다 큰 interarrival interval이라는 것을 알 수 있다.
→ An observer who arrives at an arbitary time is more likely to fall in a large rather than a small interarrival interval.
→ 따라서, Exp(λ)를 사용할 수 없다.
Back to Survey of Utilization of Town Buses.
- 우리는 [1]과 [2]에서 count한 승객의 수가 어떨지를 생각해봤었다.
- 결론은 [1] < [2]이다.
→ “Random Incidence Phenomenon”에서 봤듯이, [2]는 승객을 고르고 그 승객이 탄 버스를 알아내는 것이니까 동일한 문제이다. - 결론의 이유는 다음과 같다.
→ More likely to select a bus with a large number of riders than a bus that is near-empty.