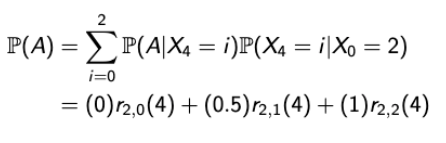Random Processes (4)

현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.

Random Processes (4)

• 지금까지 Bern, Poisson Process에 대해서 배웠다.
• 또 하나의 중요하고 유명한 Markov Chain을 이번 정리해서 해보겠다.

Definition, Transition Probability Matrix, State Transition Diagram

Recap and Markov Chain

• Discrete한 시간을 가정했을 때, Random Process는
  → RV X1, X2, …의 sequence로 볼 수 있다.
• 이 중 가장 간단한 random process는 Bernoulli Process인데, 이는
  1. Process without memory라고 볼 수 있다.
     
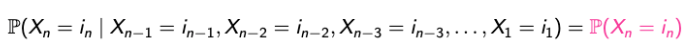
  2. 즉, 이전에 발생한 일들은 현재 일에 전혀 영향을 주지 않는다는 것을 의미한다.
• 그럼, 이것보다 just a little more general한 것은 없을까?
  → 아주 약간의 기억만을 갖고 있는 random process가 이에 해당할 것이다.
  
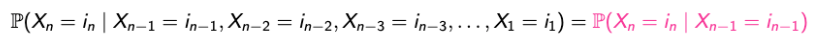
• 그리해서 나온 것이 오늘 배울 Markov Chain이다.

Example: Machine Failure, Repair and Replacement

• 예제를 통해서 Markov Chain이 무엇을 의미하는지 간략하게 생각해보자.
• 하나의 기계가 있고, 얘는 열심히 일을 한다. 그리고 이 기계는 다음과 같은 상태 변화에 대환 확률을 가진다.
  1. 현재 일을 하고 있으면, 다음 날 고장날 확률은 b
  2. 현재 일을 하고 있으면, 다음 날도 일을 할 확률은 1-b
  3. 현재 고장났으면, 수리를 받고 일을 할 수 있는 확률은 r
  4. 현재 고장 났으면, 또 고장날 확률은 1-r
• 여기서, 하루 하루의 상태를 표현할 RV Xn 을 하나 선언하자.
  
• 이렇게 하면 Conditional을 통해 다음과 같이 또 다음 날에 대한 확률을 구할 수 있다.
  
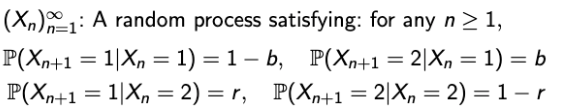
• 여기서 Markov Chain이 답할 수 있는 것은
  → What will happen at (n+1)-th day depends only on what happens at n-th day?
  

Markov Chain: Definition

• 정의 : X1, X2, …, Xn, …이 finite sample space S = {1, 2, …, m}에서의 값을 매핑할 때, S에 포함되는 i와 j 그리고 n >= 0 이면서 다음의 속성을 만족시킨다면 Markov Chain이라고 한다.
  
  → 강의에서는 finite한 sample space만을 고려하지만, 원래는 infinite까지 커버할 수 있다.
  • 또한, Alternate definition via conditional independence. For any fixed n, the future of the process after n is independent of {X1, X2, …, Xn-1}, given Xn.
• Markov Chain에서의 sample space는 state space라고도 한다.
• P(Xn+1 = j | Xn = i)는 n에 무관한 값이다.
• MC를 표현할 새로운 notation은 다음으로 한다.
  
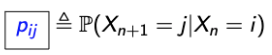
  → n에 independent하다는 것을 강조할 수 있는 아주 훌륭한 notation이다.
  
  

Transition Probability Matrix

• 새롭게 정의한 Notation은 n에 independent함을 강조하기에는 좋지만 쓰기에는 좀 별로다.
  → p1234면 12와 34? 123과 4? 흑흑
  
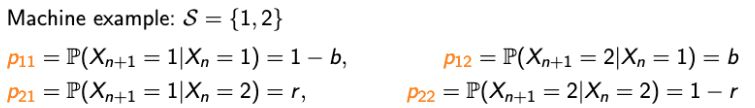
• 그래서 사람들은 매트릭스로 만드는 방법을 생각해냈다.
  
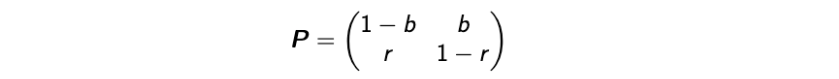
  • 이것이 Transition Probability Matrix이다.
    
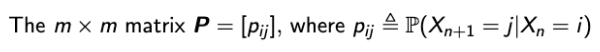
  • 여기서 하나의 중요한 특성이 있다.
    → “row”를 고정하면, “column”의 합은 1이 된다는 것이다.
    → 즉, 오늘이 고정되면 내일에 있을 일은 확률이 된다는 것이다.
    

State Transition Diagram

• 또 다른 표현 방법이다.
• State Transition Diagram
  
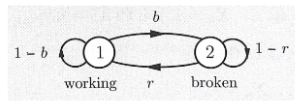
• 여기서는 Out-going의 총 합은 1이 된다.

Spider-Fly Example

• 한 파리가 1, 2, 3, 4 position에서 하나씩 옮겨가며 날라다닌다고 하자.
  🪰는 다음과 같은 확률로 움직인다.
  1. 왼쪽은 0.3
  2. 오른쪽은 0.3
  3. 가만히 있을 경우는 0.4
• 여기서, 1번과 4번에는 거미🕷가 숨어있어서 파리가 그 위치로 가면 잡아 먹히게 된다.
• Xn을 position of the fly라고 한다면, State transition diagram과 Transition probability matrix는 어떻게 될까?
  
  

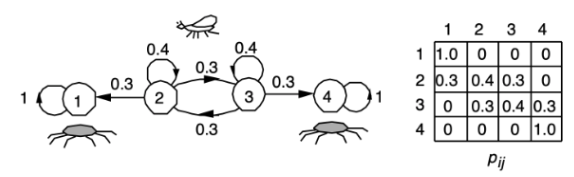
Modified Spider-fly

• 약간의 수정을 가해서 Markov Chain에서 무엇이 중요한지 확인해보자.
• 이전에 사용했던 Xn이 아닌, Yn이라는 새로운 RV로 modeling을 해보자.
  
• 흠,,그러면 Yn : n >=0 일 때, 이것이 Markov chain이라고 할 수 있을까?
  → Markov property를 사용해서 생각해보자. 즉, given Y1, Y2 ㅛ Y0 ?
  
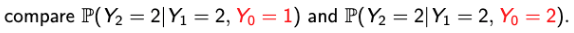
  → 우리가 배운 property를 생각해보면 두 개의 값은 같아야 한다. 내일을 알고 싶은데 어제는 필요 없으니까.
• 먼저, 좌항
  
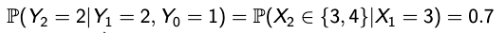
  → Y0 = 1이고, Y1 = 2가 되기 위해서는 Y0에서 위치는 3일 수 밖에 없다.
• 그리고 우항
  
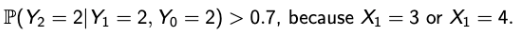
  → 같지 않다!
• 따라서, Yn : n >= 0는 Markov chain이 아니고, Markov chain을 위해선 modeling 또한 중요한 요소임을 알 수 있다.

COVID-19 Infection Example

• In discrete time slots, N persons.
• Each person is in one of the three conditions :
  (F) : infectious
  (I) : Purely infected
  (N) : Noninfected
• Infection model.
  
  → 한 사람이 N인 상태로 계속해서 있다가 어느 날 감염자를 만나게 되면
  → 해당 Time slot은 F로 변경. 단 하나의 time slot만이 해당된다. 그리고 이 때, 다른 이를 감염시킬 수 있다.
  → 이후, 격리된다.
• Contact model.
  
• 자 그러면, 모델링을 한 번 해보자잇!
  Xn : # of infectious (F) persons at the beginning of time slot n.
  Yn : # of noninflected (N) persons at the beginning of time slot n.
• Q1. Xn : n >= 0 가 Markov Chain???
  → Nope.
  
  → Xn-1 자체에서 얻어 오는 것이 아닌 Yn-1로부터 얻어지게 된다.
• Q2. Yn : n >= 0 가 Markov Chain???
  → Nope.
  
  → Xn에서 설명했던 것과 동일한 이유이다.
• Q3. Zn = (Xn, Yn) : n >= 0 가 Markov Chain???
  → Yes!
  → (Xn, Yn) only depends on (Xn-1, Yn-1).
  
  

n-Step Transition Probability

Probability of a Sample Path

• Q. What is the probability of a sample path in a Markov chain with the transition probability matrix P = [pij]?
  → 어떤 경로가 주어졌을 때, Markov chain에 의해서 이 경로로 올 확률은 어떻게 되는 것인가에 대한 질문이다.
• 어떤 경로가 다음과 같이 주어졌다고 하자.
  
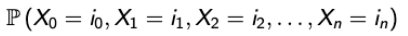
  → 이를 Conditional probability로 해석하면, P(A | B)∙P(B)로 변경할 수 있다.
  
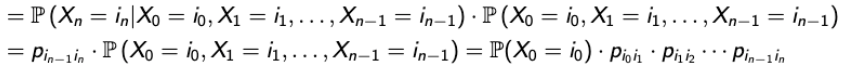
  → 하지만 Markov chain이라고 하면, n은 n-1과만 관련되기 때문에, P(A | B)는 p(i_n-1)(i_n)로 바꿀 수 있다.
  → 이후, P(B)의 항을 recursive하게 이어나갈 수 있게 되어 마지막 항의 값이 나오게 된다.
• Spider-fly 예제에서 다음과 같은 경로가 주어졌을 때의 확률(Transition probability)을 구해보자.
  
  → 👍
  
  

Prabability after n steps

• Q. What is the probability that my state is j, after n steps, starting from i?
  → 특정 구간에 해당하는 확률은 앞서 나온 내용으로 구할 수 있다.
  → “i”에서 시작해서 n번의 스텝 이후에 “j”로 끝나는 경로의 확률은 어떻게 구할 수 있을까?
• 먼저, notation을 하나 정하자.
  
  → n=1일 때는 당연히 다음 단계이기 때문에 transition probability matrix를 통해 구할 수 있다.
• 그럼, 공식으로 생각해보자.
  
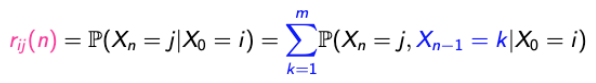
  → 처음 상태가 i이고 n번의 스텝 이후에 j의 상태로 끝나는 것은 conditional로 표현할 수 있고,
  → k가 모든 상태를 포함한다면 conditional과 마지막 항은 동일하다고 볼 수 있다.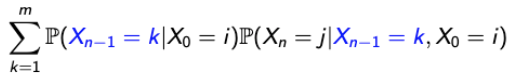
  
  → P(A, C | B) = P(C | B)P(A | C, B)공식을 통해서 풀어낼 수 있다.
  → 마지막 항에서 n과 n-1만 신경쓰면 되니까 X0=i를 없앨 수 있고
  
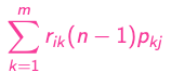
  → 마지막으로 다음과 같은 식이 도출될 수 있다.
• 따라서, r(ij)(n)은 재귀적으로 풀 수 있다는 것을 확인할 수 있고, 이것을 Chapman-Kolmogorov equation이라고 한다.

More Generalized Chapman-Kolmogorov Equation

• Chapman-Kolmogorov Equation이 더 일반적인 상황에서 어떻게 적용되는지 확인해보자.
  → n-step에서 (n+l)-step인 상황을 생각해보자.
  
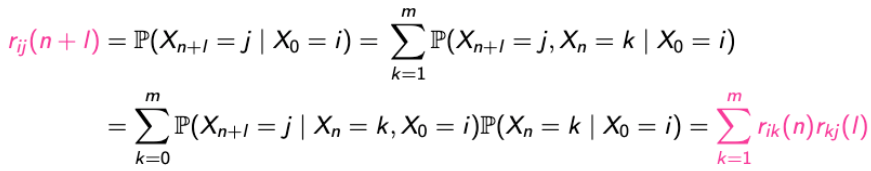
  → 앞에서 증명한 방식을 사용해서 똑같이 할 수 있다.
• Notation도 새롭게 하나 추가하자.
  
  → 이는 특정한 값이 아닌 Matrix이다.
• 과연 Matrix로 선언한 것이 어디에 좋은지 간단하게 알아보자.
  
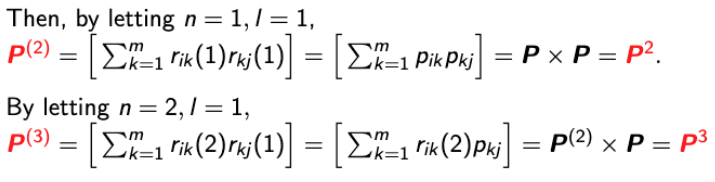
  → In other words, n-step transition probability matrix is just a n-time multiplication of the transition probability matrix P.
  

Example: Urn with Two balls

• 한 항아리는 항상 2개의 공을 갖고 있고, 이 공의 색은 Red or Blue

• 각 단계에서, 항아리에서 랜덤으로 하나의 공을 선택하고, 랜덤으로 새로운 공을 채워 넣는다.

• 채워 넣을 때,

  1. 뽑은 공과 같은 색이 들어갈 확률은 0.8
  2. 뽑은 공과 반대되는 색이 들어갈 확률은 0.2이다.
     

  이렇게 되면 공을 뽑는 것은 오직 이전 상태하고만 연관이 된다.

• 처음에 항아리는 2개의 Red 공이 들어가있다.

• Q. Find the probability the fifth ball selected is red.

• Solution.
  → Xn을 n-stage 이후에 남아 있는 빨간 공의 색으로 해보자.
  → 여기서, stage space, S = {0, 1, 2}가 된다.
  
  → 그러면, Transition Probability Matrix는 다음과 같이 생성될 것이다.
  → Let A = fifth ball is red, 그럼 매우매우 간단하게 앞서 배운 내용으로 문제를 풀 수 있다.
  
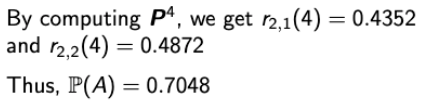
  → 4 단계 이후에 남아있는 공이 2개라면 그 중 뽑을 확률은 1이므로 1*r(2, 2)(4)
  

  → 4 단계 이후에 남아있는 공이 1개라면 그 중 뽑을 확률은 1/2이므로 0.5*ㄱ(2, 1)(4)
  

• Another Solution.