Random Processes (5)
현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.
Random Processes (5)
Classification of States
Different States and Classes?
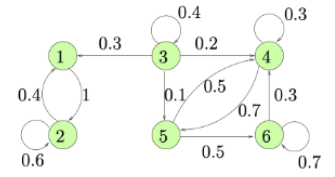
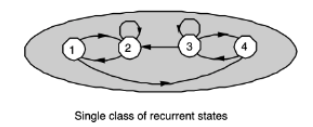
→ 다음과 같은 State Transition Diagram이 시사하는 메시지를 생각해보자.
- Multiple Classes may exist.
- State 3 can only be reached from 3.
- State 1 and 2 can reach each other but no other state.
- State 4, 5 and 6 all reach each other.
- All states can be divided into three classes : {1, 2}, {3}, {4, 5, 6}
- Some states are visited infinite times, but some states are not.
- If I start from stage 1, visit 1 infinite times.
- If I start from stage 3, visit 3 only finite times. (move to other classes and don’t return)
- States in the same class share some properties.
- State 2 will share the above properties with stage 1. (Self-visit infinite times)
Classification of States
- Accesible
- Definition : State j is accessible from state i, if for some n, r(ij)(n) > 0
→ denoted by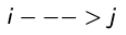
- Definition : State j is accessible from state i, if for some n, r(ij)(n) > 0
- Communicate
- Definition : If i is accessible from j and j is accessible from i, we say that i communicates with j.
→ denoted by
- Definition : If i is accessible from j and j is accessible from i, we say that i communicates with j.
- Recurrent And Trasient
- Definition : Let A(i) = {state accessible from i}, State i is recurrent, if j ∈ A(i), i is also accessible from j.
→ If A state that is not recurrent is transient. - 어렵다! i로부터 어떻게든 연결되어 있는 states(j)들이 i와 communicate할 때
- 어떤 state가 Recurrent 속성을 갖고 있으면, 그 state에서 출발을 하면 언제가는 다시 돌아오게 된다.
- Definition : Let A(i) = {state accessible from i}, State i is recurrent, if j ∈ A(i), i is also accessible from j.
Cont.
-
Recurrent 속성에 대해서 더 알아보자.
-
A set of recurrent states which communicate with each other in a class.
→ 한 집합 내에 모든 state들이 recurrent할 때, 서로 간에는 communicate할 수 있다. -
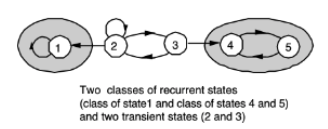
Markov chain decomposition
-
A MC can be decomposed into one or more recurrent classes, plus possibly some transient states.
-
A recurrent state is accessible from all states in its class.

-
A recurrent state is not accessible from recurrent states in other classes.
-
A transient state is not accessible from any recurrent state.
→ 위 사진과 같다. -
At least one, possibly more, recurrent states are accessible from a given transient state.
→ Transient는 쉽게 생각해서 나가는 것은 마음대로지만 들어오는게 힘들다.
-
-
The MC with only a single recurrent class is said to be irreducible.
→ 앞에 나온 것을 응용하면, All states in a single recurrent class can communicate with each other.
Periodicity
- Definition. A recurrent class is said to be periodic, if its states can be grouped in disjoint subset S1, …, Sd (d > 1) so that all transitions from Sk lead to Sk+1(or to S1 if k = d).
→ A recurrent class that is not periodic (i.e., d=1) is said to be aperiodic. - 내가 그린 이쁜 그림으로 이해해보자.
아이패드를 샀다
→ 왼쪽은 하나의 recurrent class이다.
→ 이를 우측과 같이 세 개(d=3)의 그룹으로 나눌 수 있는데, 이 그룹은 {1, 2}→{3, 4, 5}→{6}→{1,2} 이런 식으로만 움직일 수 있다. - 이것의 속성 중 하나는 n이 d로 나눠질 수 없다면 r(ii)(n) = 0가 된다는 것이다.
→ 위 그림에서,
→ r(33)(0) = 0, r(33)(1) = 0, r(33)(3) > 0, r(33)(127) > 0 - 하지만, 이러한 periodic 속성이 해당 클래스에 존재하는지를 확인하는 것은 때로는 매우 어려울 수도 있다.
→ But, 야매로 self-transition이 존재한다면 aperiodic이라는 것은 쉽게 알 수 있다.
Steady-state Behaviors and Stationary Distribution
- Markov chain을 오랜 기간 진행하다보면 steady한 상태의 행동을 확인할 수 있다.
n-step transition prob. : r(ij)(n) for large n
- 그림을 통해 n이 무수히 커질 때, Markov chain이 어떻게 되는지 확인해보자.
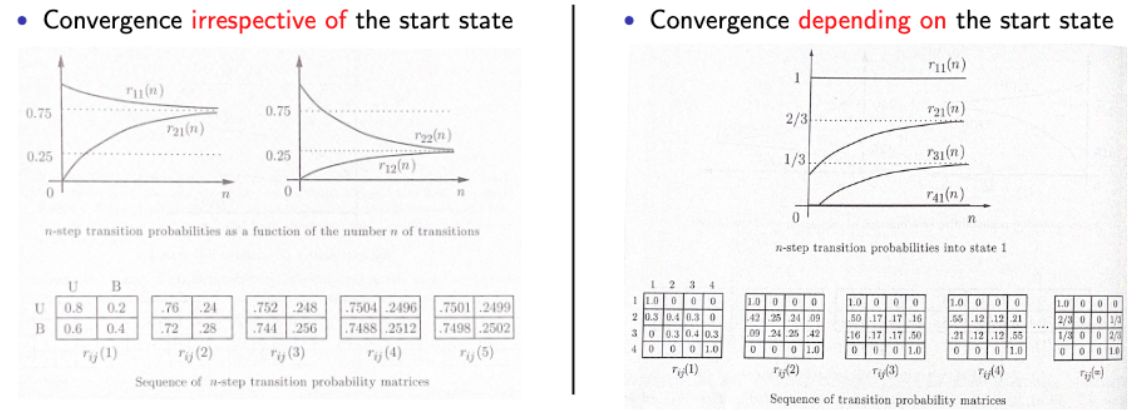
→ 출발 지점에 초점을 맞추는지/아닌지에 따른 Markov chain의 행동이다. - 여기서, 우리는 “도착 지점”에 초점을 맞춰보자
Steady-state behavior : Why Important?
- 새로운 Notation을 적용해서,
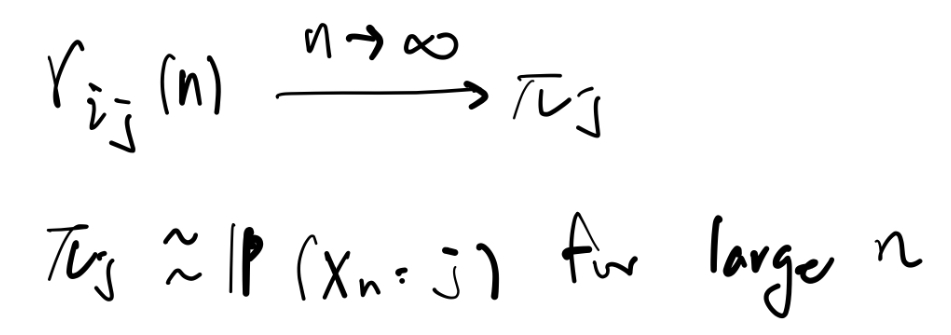
→ 다음과 같이 해보자. 이를 stationary probability라고 부른다. - 이를 사용한다면, MC를 오~랜 시간 진행시켰을 때, MC가 어떠한 최종 상태에 이르는 확률을 알 수 있다.
- 직관적으로 Machine 예제를 또 가져와보자.
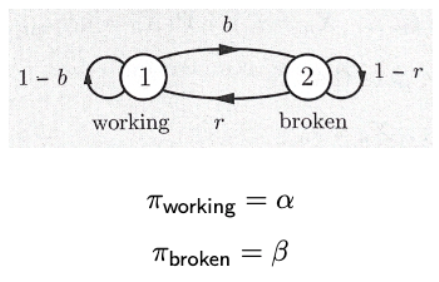
→ a+b = 1이라는 것은 명백하고,
→ 기계를 엄청나게 오래 동작시켰을 때, 얘가 계속해서 일을 잘 할 수 있는지, 아니면 죽는지를 확률을 통해 알 수 있게 된다.
Steady-state Behavior : Convergence Condition
- 이렇게 좋은 것을 그럼 언제만 사용할 수 있을까?
- A single recurrent class
- Aperiodic
- 왜 두 개의 조건을 만족해야하는지 직관적으로만 확인해보자.
- 여러 개의 recurrent class가 존재한다고 하면, 하나의 recurrent class에서는 다른 class로 넘어갈 수 없다.
→ 즉, 시작 지점을 고려하지 않을 수 없다. - Divergent behavior for periodic recurrent classes.
→ 간단하게, d=2일 때를 생각해보자.
→ r(ab)(1) = 0, r(ab)(2) > 0, r(ab)(3) = 0
→ 수렴 형태가 아닌 divergent한 형태를 보이게 될 것이다.
- 여러 개의 recurrent class가 존재한다고 하면, 하나의 recurrent class에서는 다른 class로 넘어갈 수 없다.
Steady-state Convergence Theorem
- 그럼 이렇게 좋은 것을 어떻게 계산해야될까?
→ Brute Force!!!!! - 다 해보는 것은 매우 좋지 않고 비용만 드는 문제다.
- 따라서, 두 개의 방정식을 통해 푸는 방법을 알아보자.
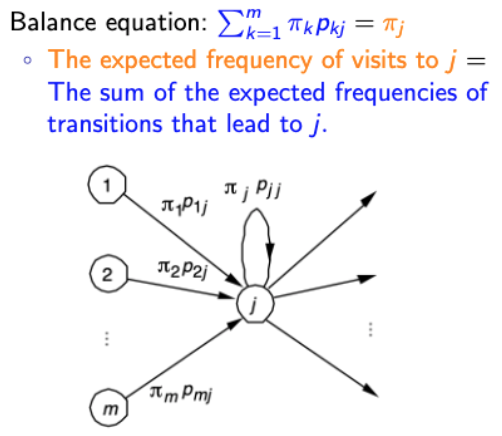
- Balance Equation
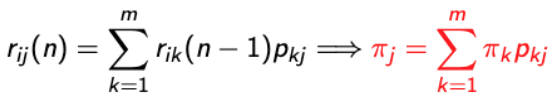
→ j = 1, 2, … m - Normalization Equation
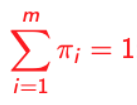
→ 결국, 확률 값이기 때문에 이들의 합은 1이 된다.
- Balance Equation
- Balance Eqn. + Normalization Eqn.을 같이 사용한다면 Linear equations을 푸는 것이기 때문에 steady-state probabiliteis의 계산이 가능하다.
Long-term Frequency Interpretation
- 직관적으로 Balance equation을 이해해보자.
- 지금까지 배운 확률이라는 개념은 다음과 같다.
→ Probability is interpreted as the relative frequencies out of many independent trials. - 이러한 개념을 convergence에 적용해보면,

- 즉, πj는 state j로의 expected fraction of time이라고 볼 수 있다.

- 그럼, 최종적으로 balance equation을 해석해보자.
Example.
- Transition Probability Matrix가 다음과 같이 주어졌을 때, π1과 π2를 구해보자!

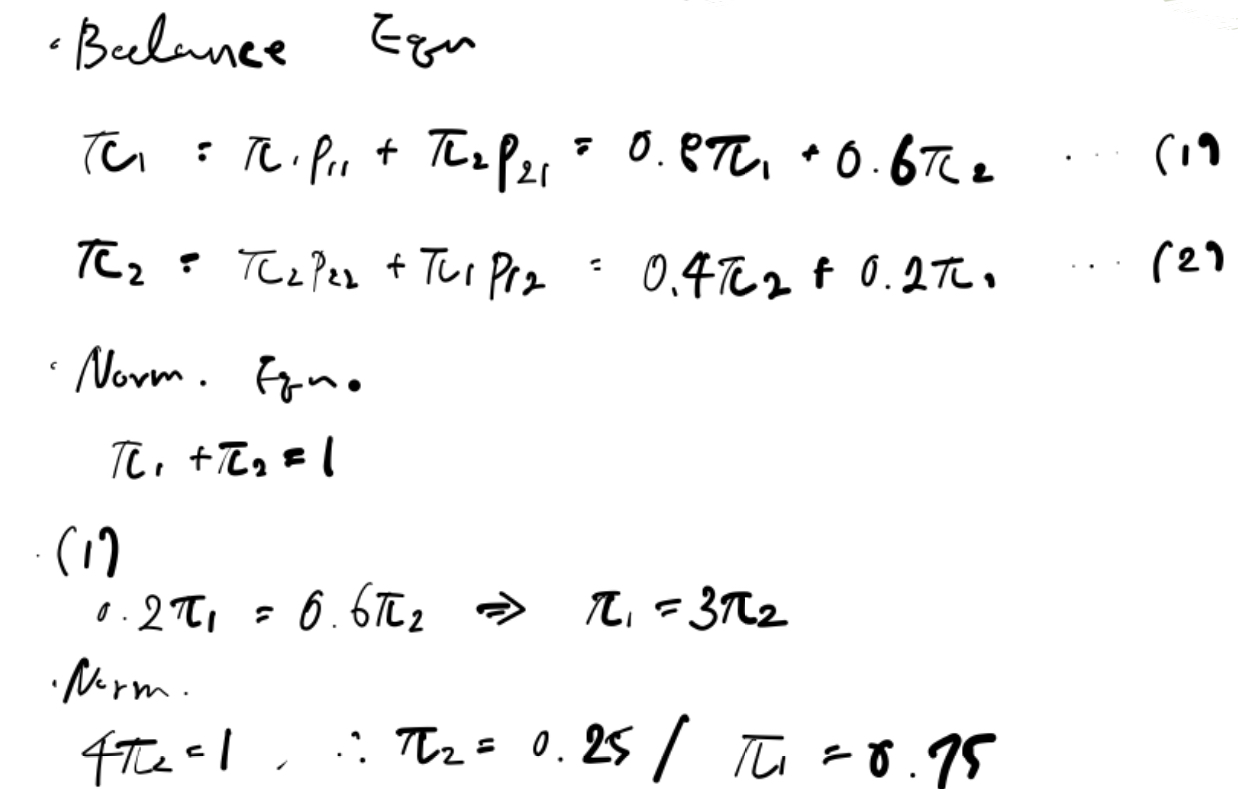
Stationary Distribution
- πj는 stationary distribution로 불리기도 한다. 왜일까?
→ Stationary : not moving or not intended to be moved.- Distribution으로 부를 수 있는가?

- Stationary라고 부를 수 있는가?
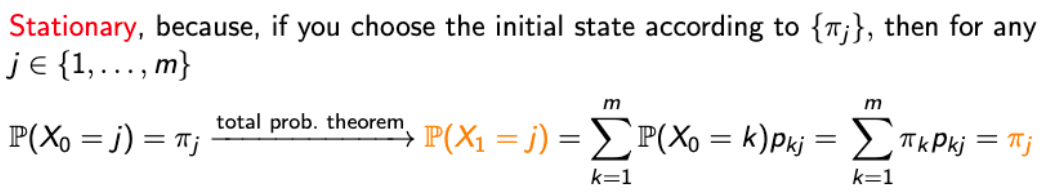
→ 원래는 출발점을 고려하지 않았지만, πj에 따라서 출발 지점을 선택 했을 때는 위와 같은 결과가 나온다.
→ 나의 생각으로는 Long-term frequency interpretation에서 나온 것처럼 애초에 πj라는 것이 모든 경우를 포함하기 때문…?
- Distribution으로 부를 수 있는가?
- 확장해서 다음과 같은 것을 알 수 있다.
- 그럼 이 좋은게 항상 모든 것에 적용이 가능할까?
→ 좋은 것은 그렇지 않다.- Only single recurrent class
- Aperiodic
Example.
-
한 사람은 우산을 두 개 가지고 있고, 집에서 사무실로 또 그 반대로 우산을 가지고 다닌다.
-
만약 비가 내리고, 우산이 있다면 그 우산을 갖고 가지만, 비가 오지 않으면 우산을 그냥 내비 두고 간다.
- 집 : 2 / 사무실 : 0
→ 출근(🌧) : 집 : 1 / 사무실 : 1
→ 출근(☀️) : 집 : 2 / 사무실 : 0
→ 퇴근(🌧) : 집 : 2 / 사무실 : 0
→ 퇴근(☀️) : 집 : 2 / 사무실 : 0 - 집 : 1 / 사무실 : 1
→ 출근(🌧) : 집 : 0 / 사무실 : 2
→ 출근(☀️) : 집 : 1 / 사무실 : 1
→ 퇴근(🌧) : 집 : 2 / 사무실 : 0
→ 퇴근(☀️) : 집 : 1 / 사무실 : 1 - 집 : 0 / 사무실 : 2
→ 출근(🌧) : 집 : 0 / 사무실 : 2
→ 출근(☀️) : 집 : 0 / 사무실 : 2
→ 퇴근(🌧) : 집 : 1 / 사무실 : 1
→ 퇴근(☀️) : 집 : 0 / 사무실 : 2
- 집 : 2 / 사무실 : 0
-
비가 올 확률은 p이다.
-
Q. What is the steady-state probability that she gets wet during a commute?
- State space = {0, 1, 2} : i umbrellas available in location.
→ 즉, 상태의 변화는 출근 또는 퇴근이 된다. - Transition diagram
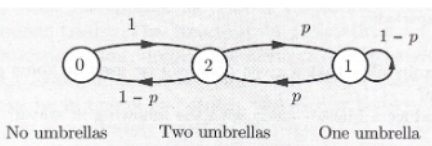
→ 상태의 변화는 출근 또는 퇴근임을 기억하자.
→ 예시로, 0에서 2로 가는 것은 출근 때 집에 0개이지만 사무실에는 2개가 있으니 1의 확률이 된다. - 이는 single recurrent class이고 aperiodc(self-transition)이므로 우리가 배운 내용을 모두 적용할 수 있다.
- Using Balance and Normalization equation.
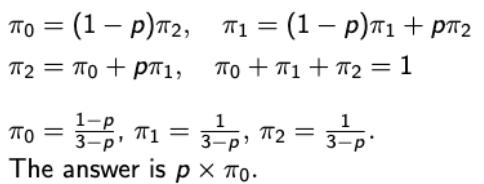
- State space = {0, 1, 2} : i umbrellas available in location.
Birth-Death Process
Example 1. Random Walk with Reflecting Barriers
- 한 사람이 직선의 길을 걷고 있다고 해보자.
- 그리고 이 사람은 각 slot time에서 오른쪽으로 갈 확률은 b, 왼쪽으로 갈 확률은 1-b라고 해보자.
- 직선의 길이는 m이고 직선에서의 위치는 1, 2, …, m으로 표현하고 그 중하나의 위치에서 시작한다.
- 이 때, 0의 위치(1의 위치에서 왼쪽으로 또는 m의 위치에서 오른쪽)에 도착했을 때, 즉시 방향 전환하기 직전의 위치로 가게 된다.
- Q. 이 때의 Transition Diagram은?
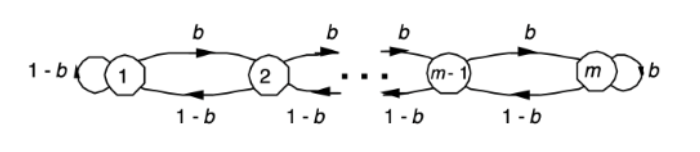
Example 2. Queueing
- 손님이 슈퍼 마켓에서 계산을 위해 카운터로 간다.
- 카운터에 줄을 설 수 있는 최대 인원 수는 m이고, 앞선 손님이 있고 m이 아니라면 기다리게 된다.
- 이러한 condition에서는 3가지의 상황이 발생할 수 있다.
- 새로운 손님이 b의 확률로 도착
- 이미 줄에 있던 사람이 d의 확률로 떠남(계산 또는 다른 물건을 가지러)
- 줄에 1-b-d의 확률로 그 누구도 새로 오지 않고 떠나지 않음
- Q. 이 때의 Transition Diagram은?
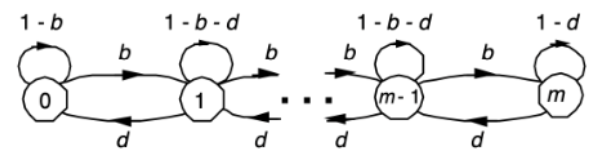
Birth-Death Process
-
앞서 본 두 예제의 공통점이 무엇일까?
→ 바로 근처의 이웃과만 transition이 발생한다는 것이다. -
이러한 Markov chain을 Birth-death process라고 부른다.
- Linearly arranged
- Transition only occur to a neighboring state
-
State Diagram of Birth-Death Process
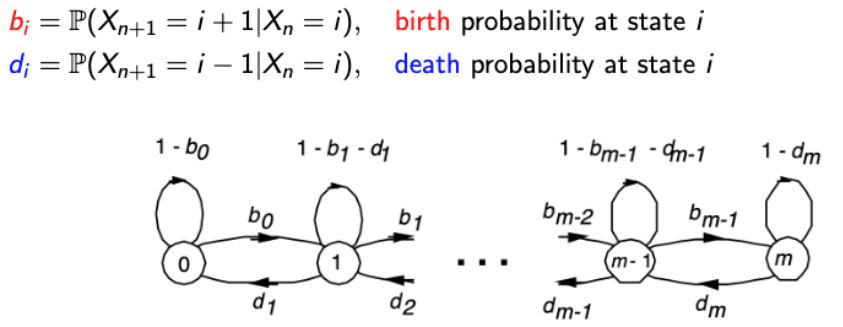
→ 앞서 다룬, Random Walk와 Queueing은 Birth-Death Process의 특이 케이스 중 하나이다. -
Balance Equation.
-
at state 0.
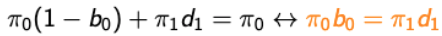
-
at state 1.
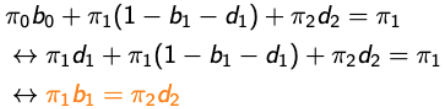
-
General.
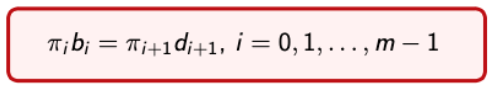
-
이 식으로부터 우리가 유추할 수 있는 것은 state n의 관점에서 dn, bn의 frequency는 동일하다는 것이다.
→ 따라서, Birth-Death Process에서는 이를 Local balance equation이라고 한다. -
특이한 Balance Eqn.을 갖고 있기 때문에 stationary probability를 구하는 것도 간단하게 할 수 있다.
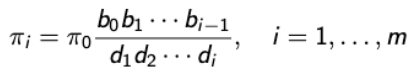
→ 추가로, 당연히
-
Transient behaviors
Motivating Questions
- 이 전까지는 Steady-state behavior에 대해서 공부를 했었다.
→ 하나의 recurrent class 🏝 - 이제는 더 확장된, 그리고 일반적인 MC에 대해서 생각해보자.
→ A MC with multiple recurrent class and a set of transient states T. - 여기서 그럼 하나의 가정을 진행해야 한다.
→ 이 MC가 어디서 시작해야될까?- Recurrent class
→ 한 번 빠지면 헤어나올 수 없다. (탈모) - Transient state
→ 그러면 언젠가는 Recurrent class로 진입하게 될 것이고, 거기서 재밌게 놀 것이다.
- Recurrent class
- 그래서 우리는 일반적인 MC에서 이러한 질문을 던질 수 있다.
→ Q. Transient Behavior : What is the first recurrent state to be entered as well as time until this happens?
Special case : Every Recurrent State is Absorbing
-
General한 형태를 다루기 전에, 특이한 케이스를 하나 살펴보자.
→ Every recurrent state is absorbing -
Definition. A state k is absorbing, if p(kk) = 1, and pky = 0 for all j != k.
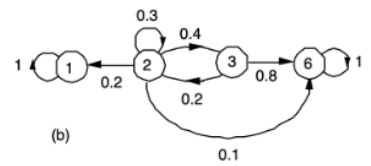
→ 여기서는 1과 6이 해당된다. -
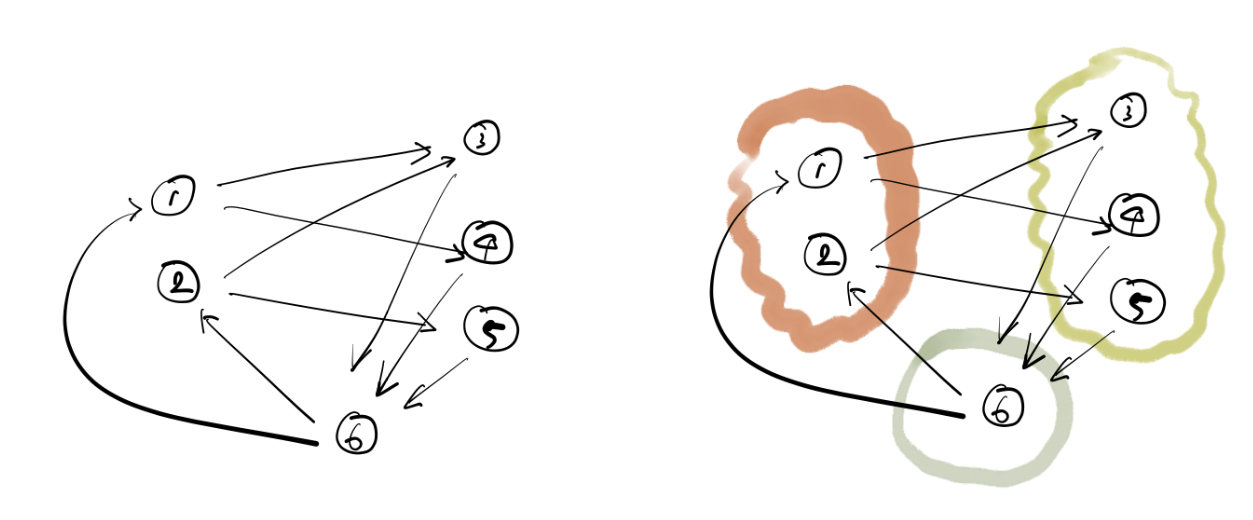
For a given absorbing state s, the probability ai = ai(s) of reaching s, starting from a state i?
→ i : starting point
→ s : End point, absorbing state -
S = 6으로 고정시켰을 때,
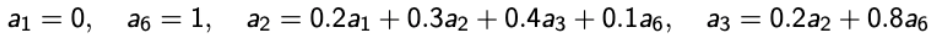
→ (s는 생략) 위 그림에서 각각의 ai의 확률은 위와 같다.

→ a2(1) = 1 / a2(6)가 된다. 1로 가려면 2를 무조건 거쳐야 하고,→ 6이 absorbing한 것처럼 1도 absorbing하기 때문.
For General MCs
-
다음 그림을 봐 보자.
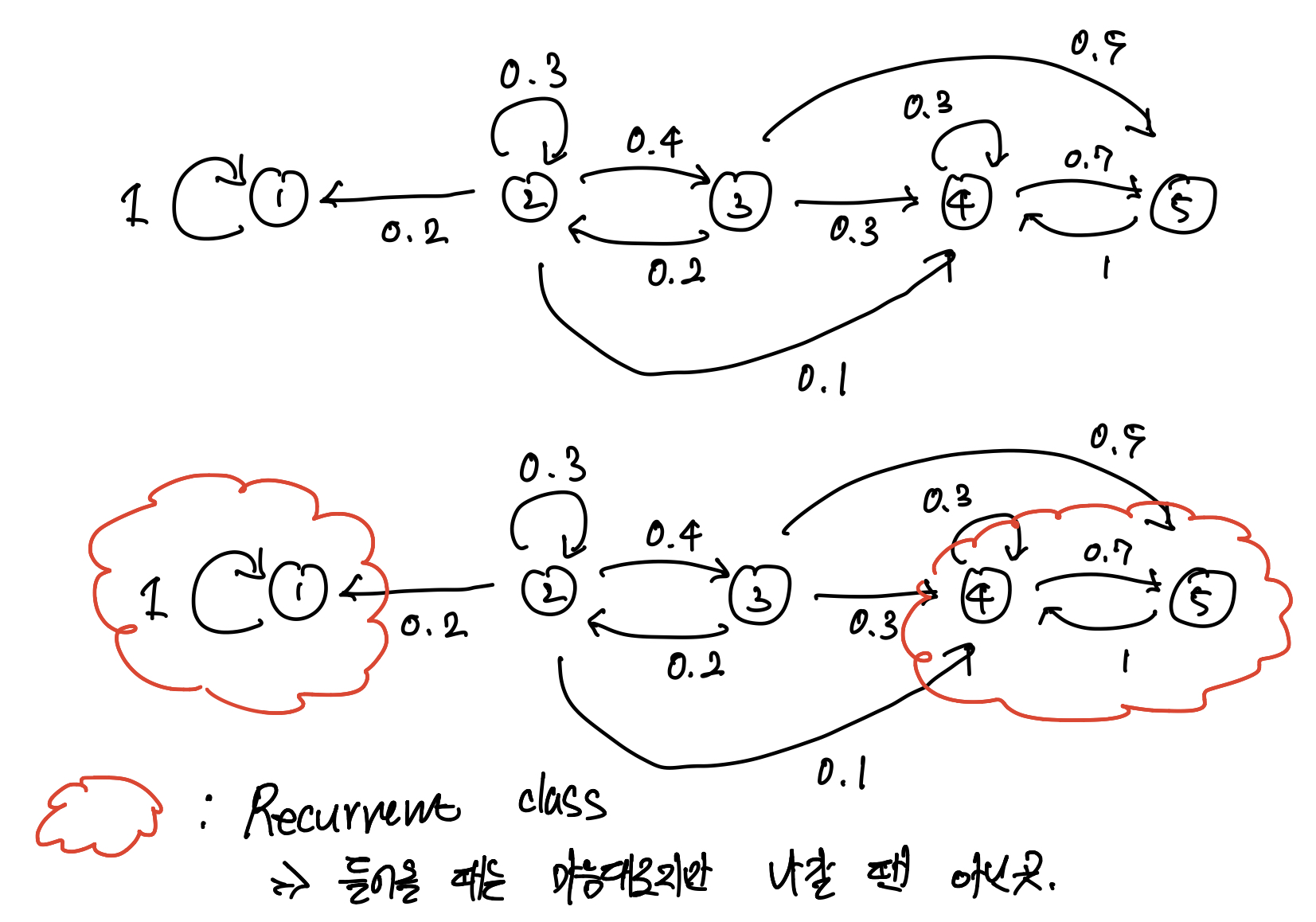
-
{1}과 {4, 5}는 Recurrent class로서 한 번 들어오면 다시는 나갈 수 없는 구조이다.
-
그럼 여기서 질문.
→ Probability that the state eventually enters the recurrent class {4, 5}?
-
-
{4, 5}는 들어가는 순간 나올 수 없기 때문에, 단순히 그 ‘섬’으로 들어갈 확률을 구하는 문제이다.
-
그럼, {4, 5}를 하나의 섬, 즉 {6}으로 치환해도 별 다를 것이 없는 문제가 된다.
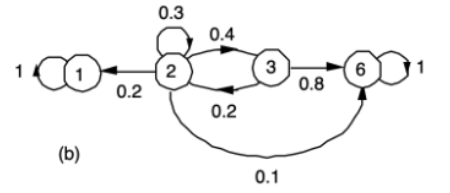
→ 문제에 대한 정답? 우린 이미 구했다. 위를 보자!
Expected Time to Any Recurrent State
-
Question. Starting from a transient state i, what is the expected number of steps until a recurrent state is entered(which we call absorption)?
- Special case when all recurrent states are absorbing
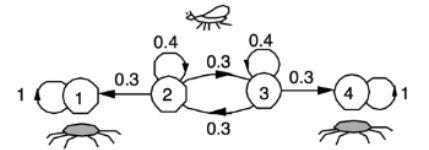
→ Spider-Fly! - μi를 새롭게 정의해서,

- 그럼 문제에 대한 정답은 다음과 같다.
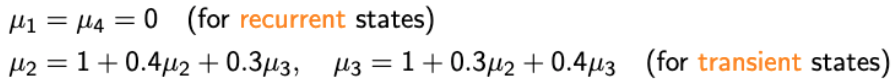
- Special case when all recurrent states are absorbing
Expected Time to a Particular Recurrent State s
- 풀이의 용이성을 위해 Single recurrent class를 생각하자.
- 우리는 두 개의 질문을 할 것이다.
Q1. Mean first passage time. Starting from i, expected number of transitions to ti to reach s for the first time.
Q2. Mean first recurrence time. Starting from s, expected number of transitions to ts* to reach s for the first time. - 가정하는 MC는 다음과 같다.
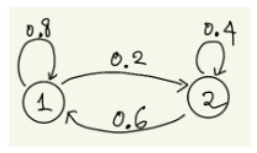
- 풀이는 다음과 같다.
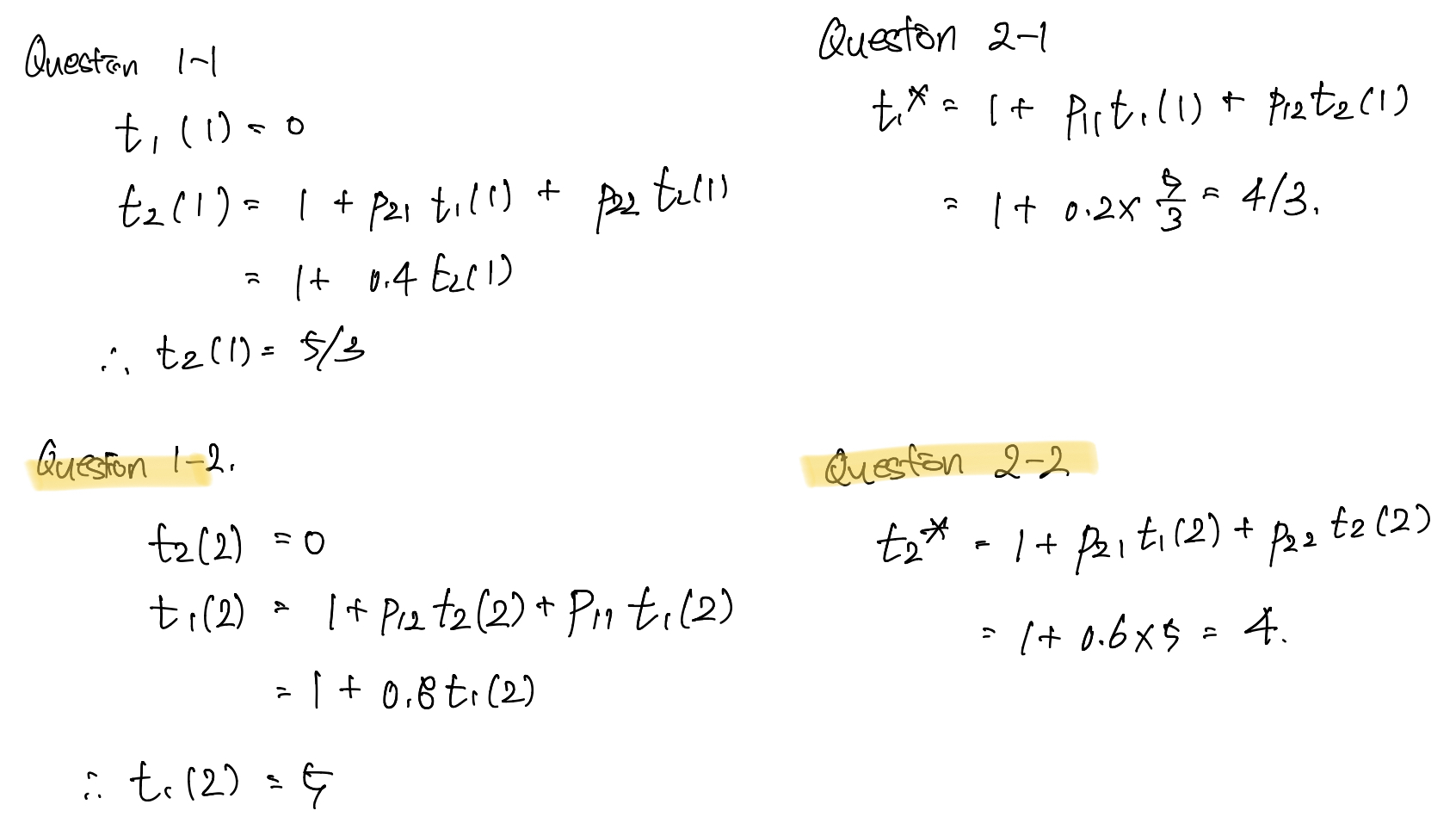
→ 1-2와 2-2는 내가 풀어서 넣었다. 틀릴 수도 있당.