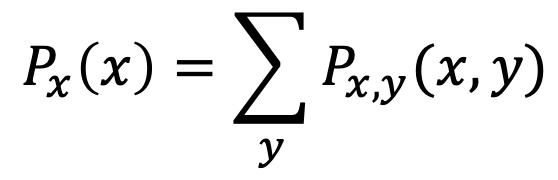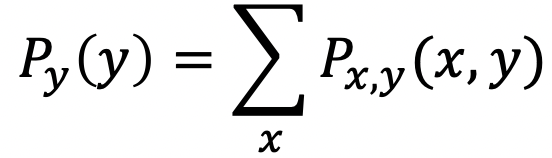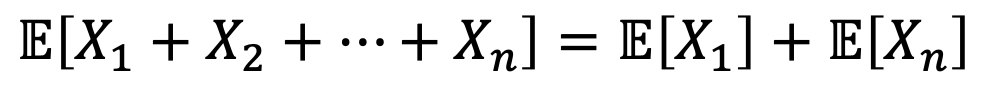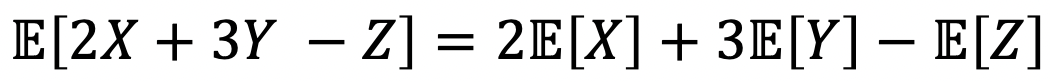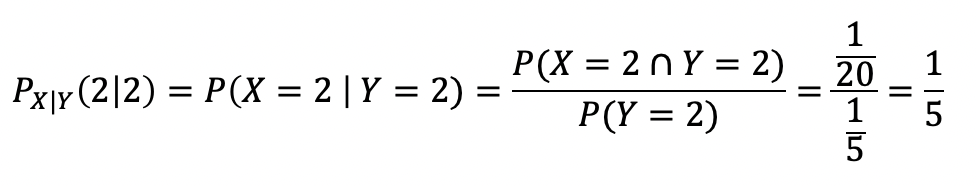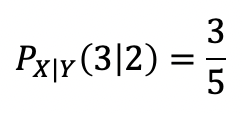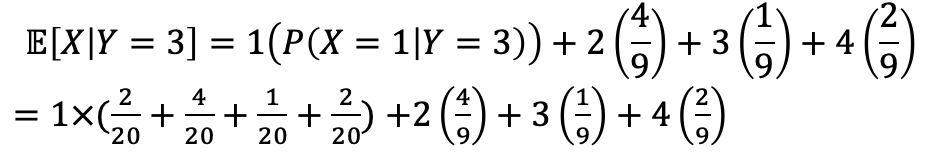Random Variables (2)

3 minute read

Random Variable (2)

현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.

시작하기 전 (1)에서 한 내용을 복습하고 갑시다.
1. Random Variables(X)는 어떤 이벤트 w에 대한 값을 실수(x)로 mapping해주는 ‘함수’이다.

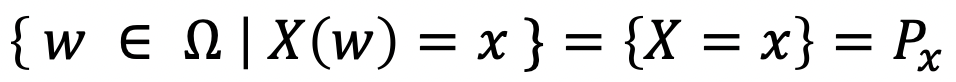
(Functions of) Multiple random variables

Joint PMF
- For two random variables X, Y, consider two events {X=x}, {Y=y}, and
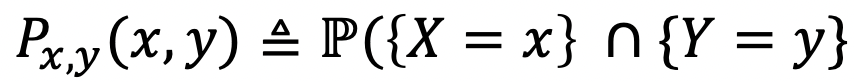
- 그러면 얘는 이러한 속성을 갖게 된다.
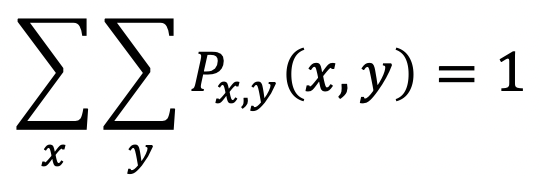
- 또한, 얘에서 어떤 속성을 갖게 되면 Marginal PMF라고 불릴 수 있다.
Marginal PMF
- Joint PMF에서 아래 두 속성을 만족한다면 Marginal PMF이다.
Functions of Multiple RVs
- Z라는 Random Variable이 있다고 해보자, 그리고 Z = g(X, Y)로 rv인 X, Y와 g라는 함수를 통해 표현된다.
  → X+Y , X^2 + Y 등이 될 수 있다.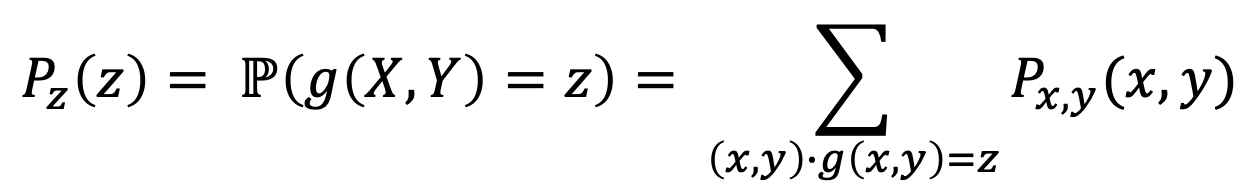
  - 그렇다면 이렇게 표현될 수 있다!
  - 여기서, Pz를 위해 시그마 연산에서 X와 Y, g를 통해 만들어질 수 있는 모든 값을 사용한다는 것을 명심하자.
- 그럼 이 친구의 Expectation은 어떻게 표현될까? 비슷하다.
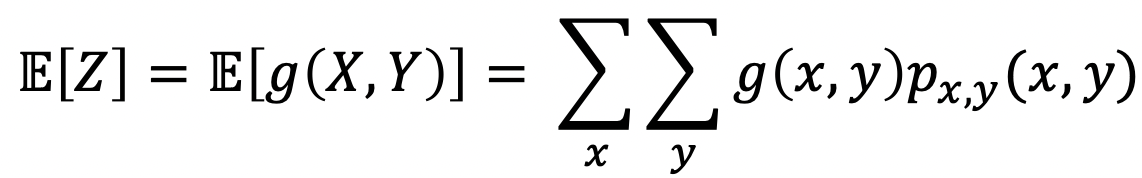
Linearity of Expectation for Multiple RVs
- (1)에서 말했던 것과 같이 Expectation은 다음과 같은 속성을 갖고 있다.
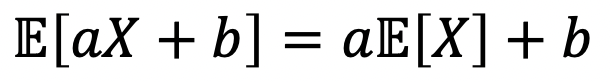
- 이에 따라서, Multiple RVs에서는 다음과 같은 속성을 가질 수 있다.
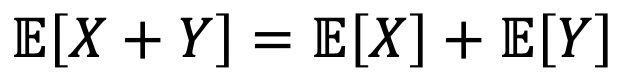
- 또! 여기서 확장해보자.
- Linearity를 사용하여, Mean of a binomial rv Y with (n, p)를 구해보자.
  → Y = number of success in n Bernoulli trials with p
  - 그렇다면, Y = X1 + X2 + … + Xn으로 표현될 수 있고, Xi = Bernoulli rv라고 할 수 있다.
  - 여기서, Y의 Expectation을 구해보자.
    
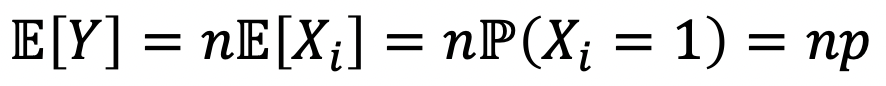
    → Bernoulli rv에서 P(X=1)로 표현됨을 기억하자…
    → Bernoulli rv는 단순히 ‘성공’ 또는 ‘실패’로 나타나는 실행(bernoulli trials)을 n번 반복했을 때, 성공이 나타난 횟수를 확률 변수로 갖는 것
    → 각 실행은 서로에게 어떤 영향도 주지 않음

Conditioning of random variables

이전 내용을 복습하자면, probability law에는 두 가지의 종류가 있고, 이는 Normal과 Conditional이다.
둘 다, 3 axioms를 만족시키며 다음과 같은 속성과 notation을 갖고 있다.
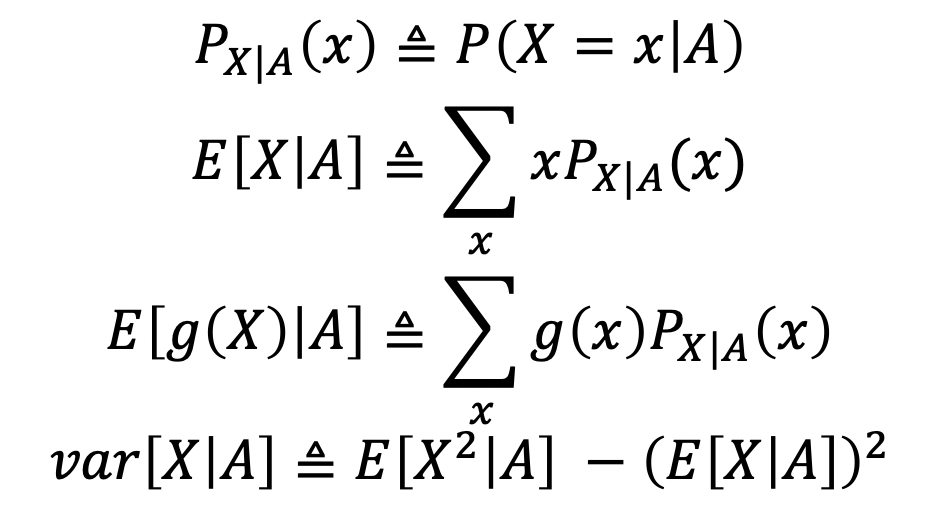
하지만 얘네가 모두 단순히 notation임을 기억하고, 우변이 나오게 된 이유에 대해서 잘 알고 있자.
1. Normal과 Conditional에서의 E와 var
  - 공통적으로 x={1, 2, 3, 4}를 뽑게 되고, 각각은 동일한 확률로 뽑힌다.
  - Normal
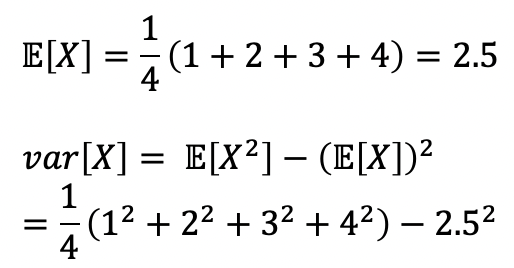
  - Conditional, 조건 : X >= 2
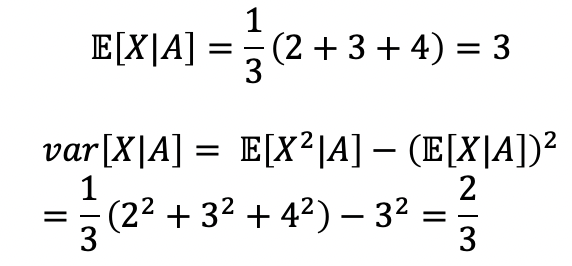
    - X>=2에서는 P_X|A(1) = 0이 됨을 이해하자, 그렇게 되면 모두 동일한 확률을 갖게 됨으로 P_X|A(-) = 1/3이 된다.
Conditioning on Event VS Conditioning on RV


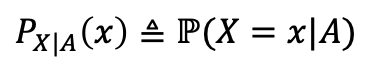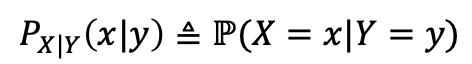- Conditioning on Event	- Conditioning on RV

→ Y=y를 A라고 생각한다면 동일한 Notation에서의 수식을 얻을 수 있다!

Conditional PMF
- Conditional PMF
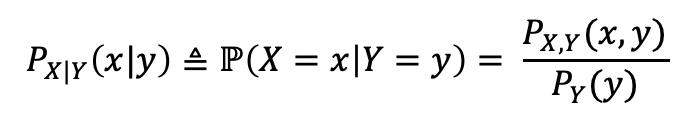
  - P(A B) = P(A ∩ B) / P(B) 인데, P(A ∩ B)를 Joint PMF로 표현할 수 있다.
- Multiplication rule
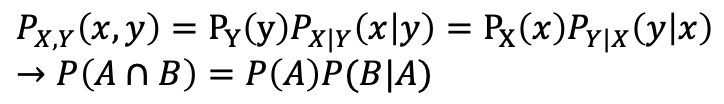
- 예제를 풀어보자
  - 다음은 tetrahedral 주사위를 던졌을 때, 두 면의 숫자에 따른 확률이다.
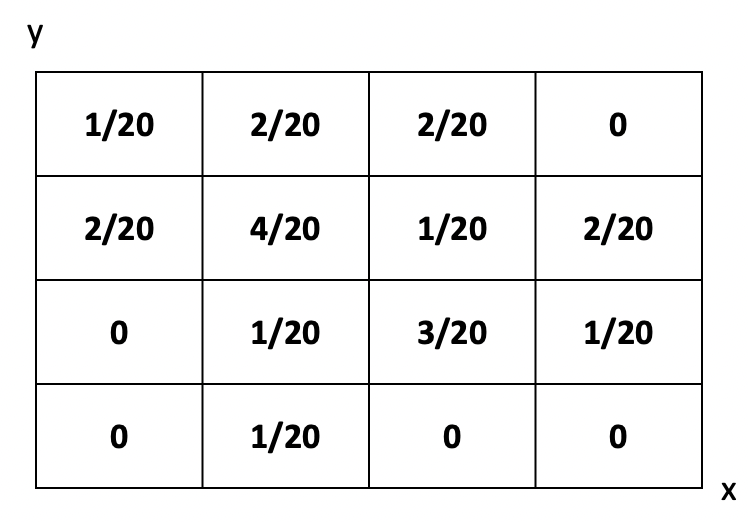
- Total Expectation Theorem for {Ai}
  - 여기서 잠깐! TPT에 대해 복습을 해보고 들어가자.
    → Sample space를 mutually exclusive하게 partition({A1,…An})으로 나눴을 때, P(B) = ΣP(Ai)P(B | Ai)를 만족한다.
  - 이거를 Conditional PMF에 적용해보자.
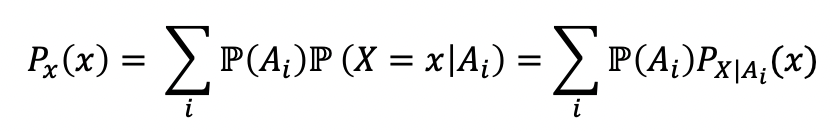
    - 그러면 이렇게 된다. 이걸로 Expectation을 계산해보자.
    - Expectation은 기댓값, 확률적 평균을 의미하니까 각 나온 TPT에 시그마를 붙여 계산한다.
      → Conditioning of random variables 에 대한 정리를 위에서 살펴보면서 하면 된다.
  - Total Expectation Theorem
    
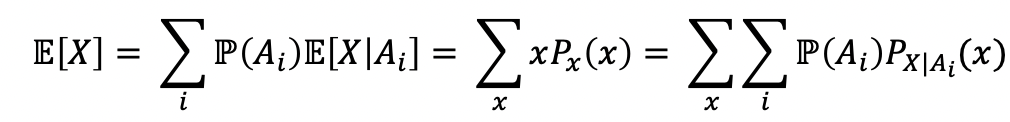
    → 이전에도 했듯이, 얘는 가중치를 더한 형태가 된다. 하지만 가중치와 기댓값이 곱해질 때(2번째 변), 각 Ai에 대한 값이 곱해짐을 확인해야 한다.
    
    → 물론, Conditioning on Event VS Conditioning on RV 에서 설명한 것 처럼 Ai는 Y=y처럼 다른 Random Variable로 변환될 수 있다.
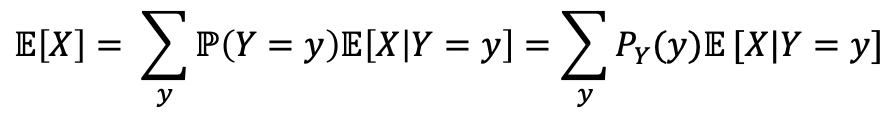
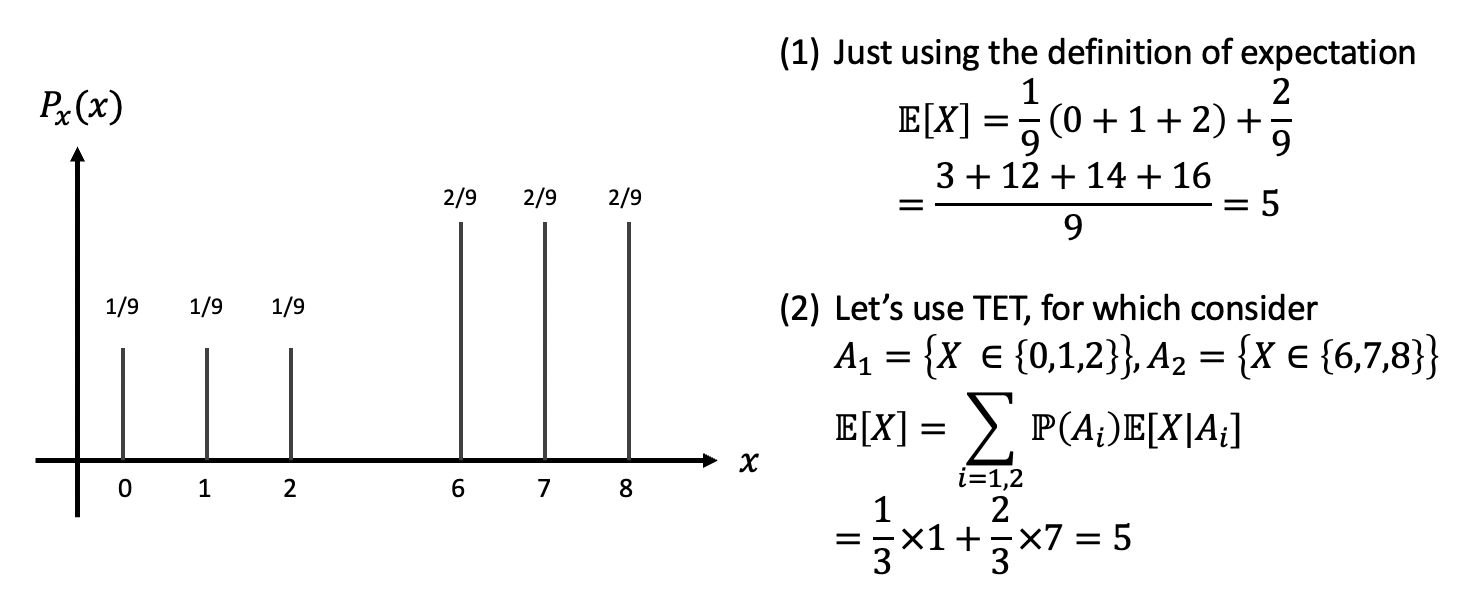
    - 이에 대한 예제를 살펴보자,
Memoryless Property
- Some RVs often do not have memory. → 말 그대로 기억력이 없음을 의미
- 예시를 통해 이 말을 이해해보자.
  
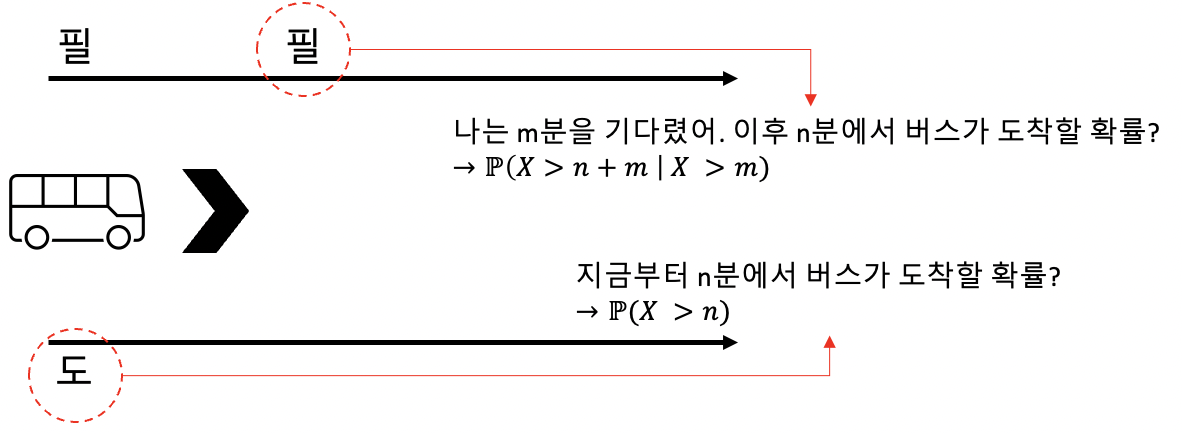
  → 필은 m분을 먼저 기다린 뒤, n분 후에 버스가 도착할 확률을 궁금해 하고 있다.
  
  → 도는 지금부터 n분 후에 버스가 도착할 확률을 궁금해 하고 있다.
  
  → 이 둘은 결국 같은 질문이고, 필이 m분을 기다렸다는 것은 사실상 영향을 주지 않는다.
- Definition. A random variable X is called memoryless. If, for any n, m >= 0
- Meaning. Conditioned on X > m, X - m ‘s distrubution is the same as the original X.
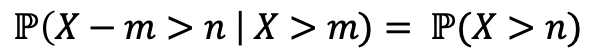
- 모든 RV가 이를 만족하는 것은 아님
- Memoryless Porperty of Geometric RVs
  → Geometric RVs는 무한히 많은 independent한 시도 끝에(k번의 시도) 성공하는 확률을 의미
  → 그리고 아래와 같은 식을 만족한다.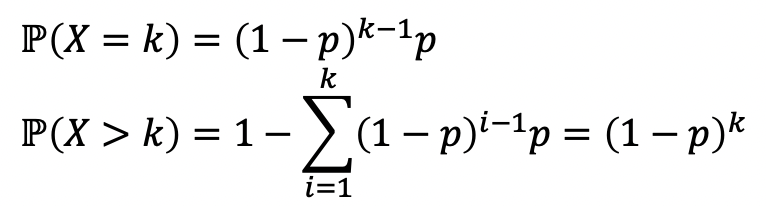
  - 그럼 이 친구가 항상 memoryless라고 가정을 해보자.
    
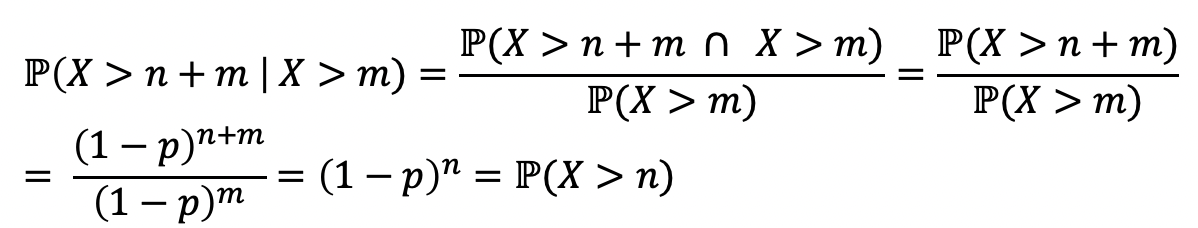
    → 짜잔, 이렇게 증명이 되고 Geometric RV는 항상 memoryless임을 알 수 있다.
  - 그럼 또, 이 친구가 좋은 친구인 이유를 아래 예시를 보면서 확인해보자.
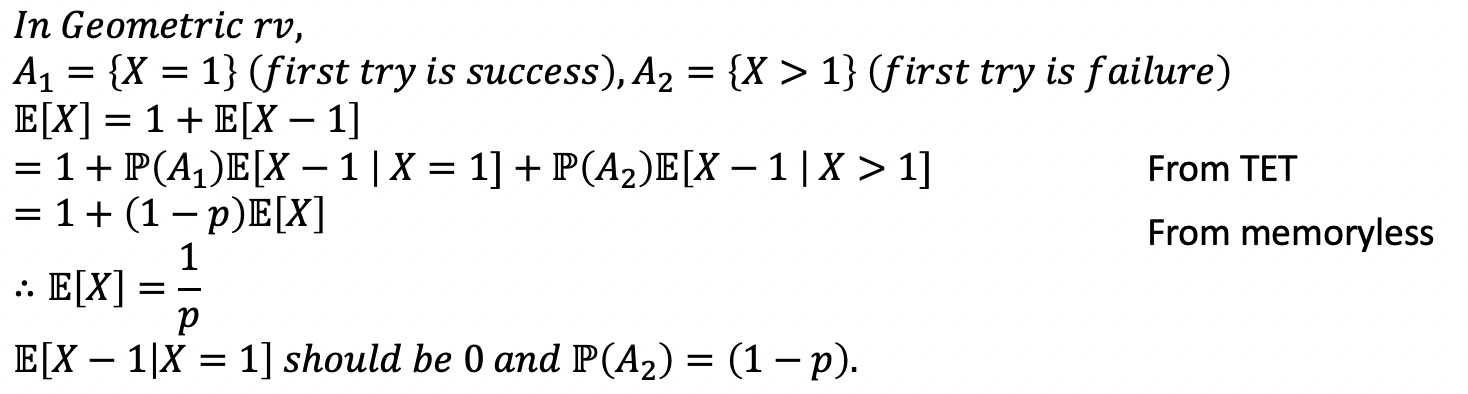