Random Variables (3)

1 minute read

Random Variable (3)

현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.

Independence for random variables

Independence에 대해서 다시 한 번 보자

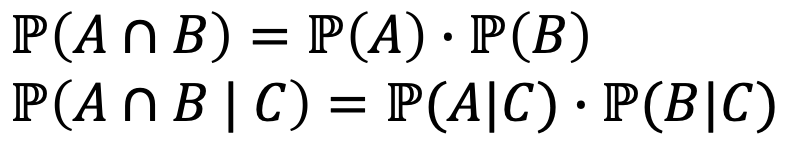
→ 다음과 같은 식을 만족한다면 [Conditional] independence 하다고 말할 수 있다.
그럼 Random Variable과 event의 independence는 어떤 조건을 가져야 할까?

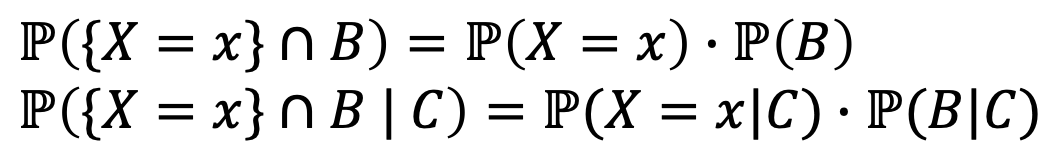
→ 당연히, 비슷한 형태를 갖게 된다.
추가적으로, 두 개의 RV에 대한 independence는 어떤 조건일까?

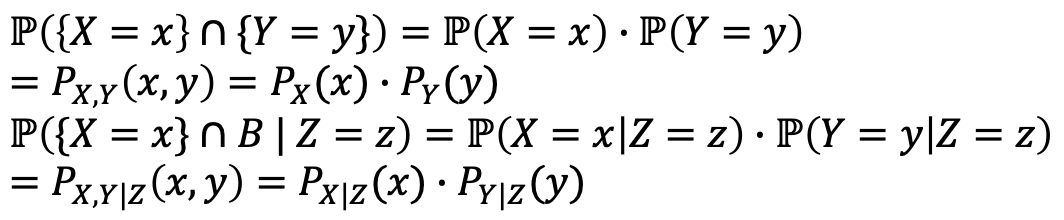
→ 이것 또한 비슷한 형태를 갖게 되고, 지난 시간에 봤던 Joint PMF를 사용한 notation을 다시 한 번 숙지하자.
예제를 통해 이해를 해봅시다~~

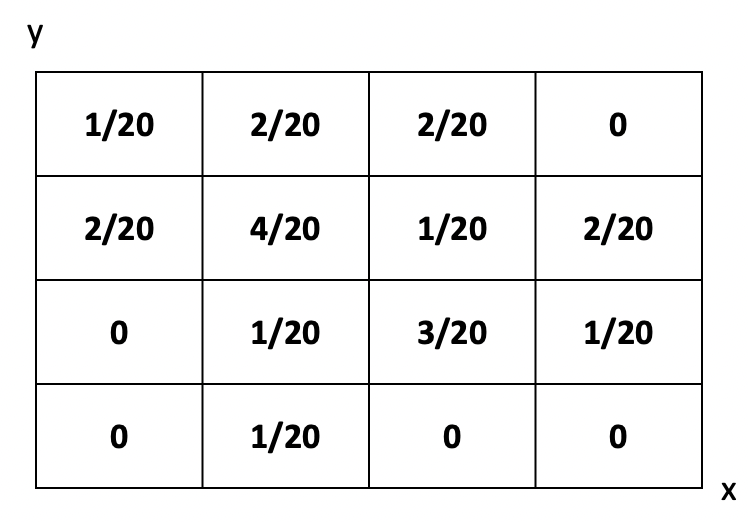
→ 익숙한 그림이다……….

1) X ㅛ Y ?

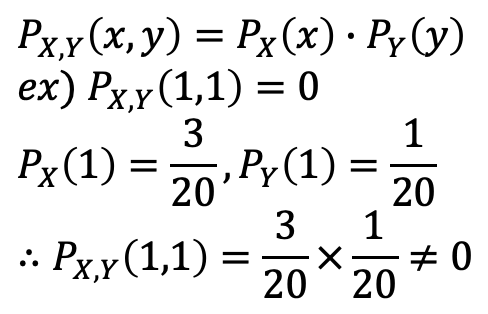
2) X ㅛ Y | {X <= 2 and Y >= 3} ?
- 조건을 Z라고 말한다면, 다음과 같은 수식을 만족해야 한다.
  
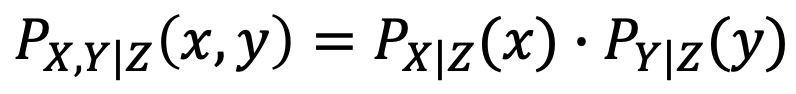
  → 자, 그러면 Z 조건에서 발생할 확률은 다음과 같이 채워지게 된다.
  
  → 여기서 중요한 점은, ‘Z 조건’에서 발생할 확률이기에 분모가 달라진다는 것이다.
- 그럼 계산을 해 보십다!
  1. X=1이고 Y=3일 때. (1/3)*(2/3)=2/9이다.
  2. X=2이고 Y=4일 때, (2/3)*(1/3)=2/9이다.
  3. 나머지도 똑같다^^, 따라서 independence이다.
Expectation과 Variance에서 Independence
- Expectation
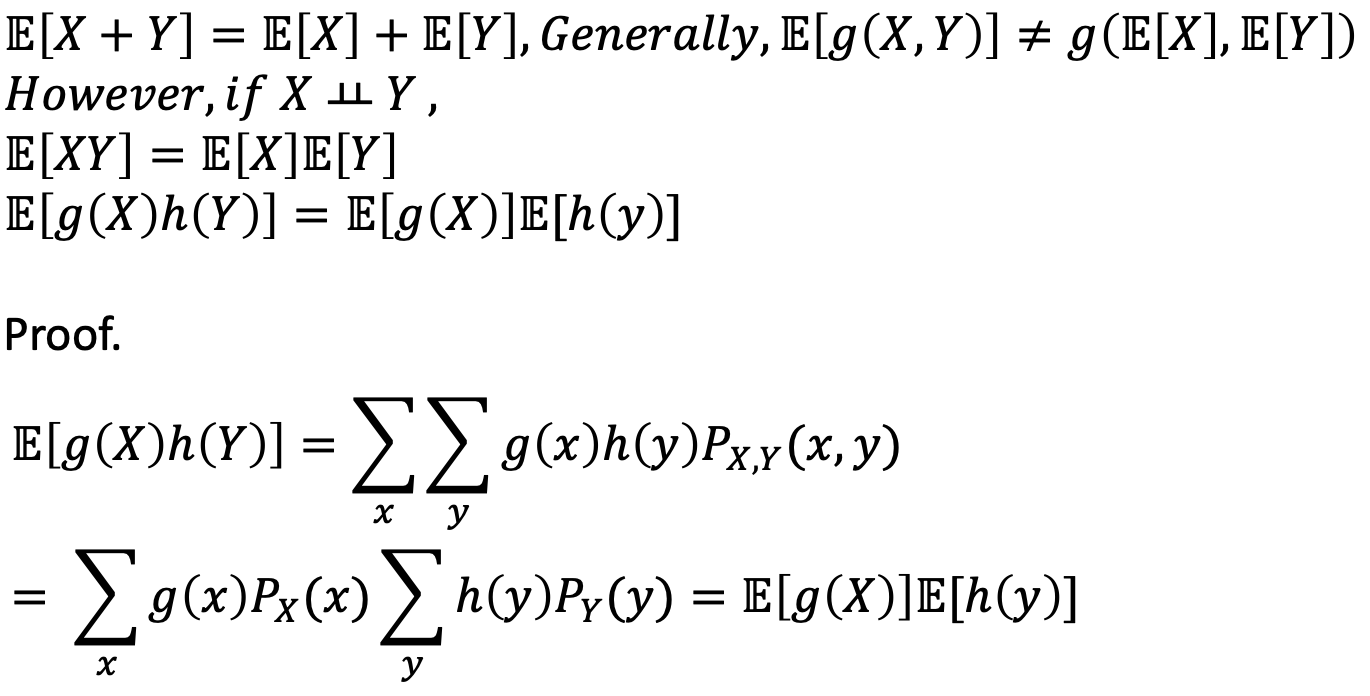
- Variance
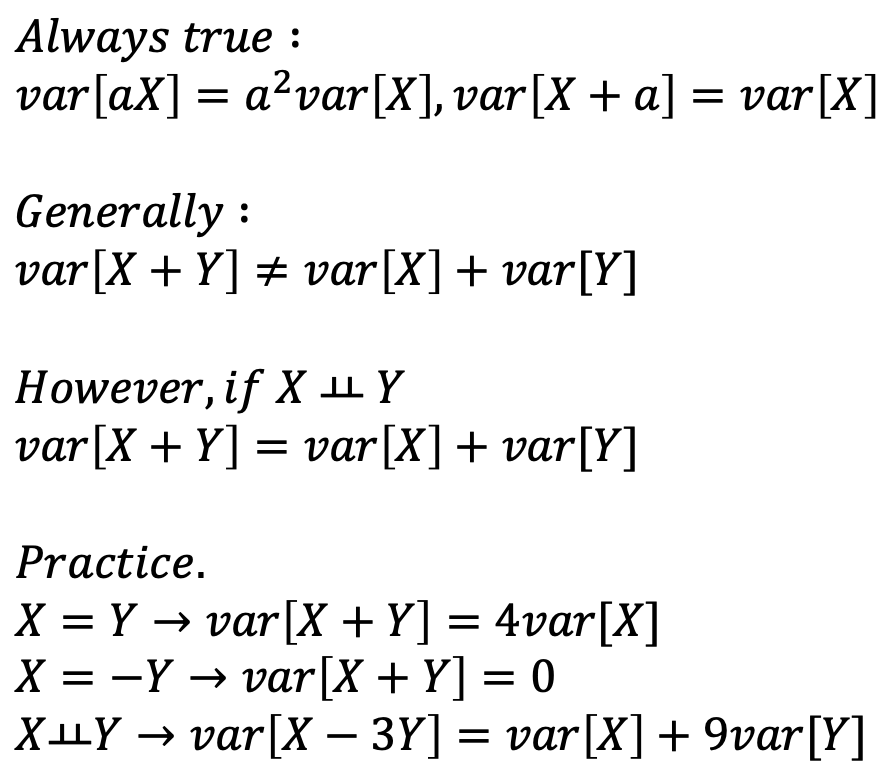
  - 여기서, 일반적으로 var[X+Y] != var[X] + var[Y]인 이유를 확인해보자. (var의 정의를 사용하면 쉽게 생각할 수 있다.)
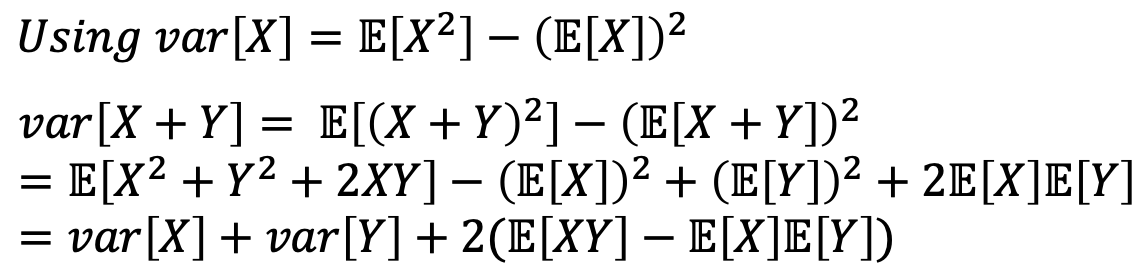
  - 감이 오지 않는가,
    X ㅛ Y이기 위해서는 var[X+Y] = var[X] + var[Y]이니까,
    E[XY] = E[X]E[Y]를 만족하면 된다.💩
- 하나의 예제를 살펴보자.
  
  n명의 사람이 모자를 어떤 박스에 던진다.
  
  그리고 박스에서 랜덤하게 하나의 모자를 꺼낸다.
  
  이 때, rv X를 자기 자신의 모자를 꺼낸 사람(1)이라고 해보자.
  
  이 때, E[X], var[X]를 구하라.
  1. Define a rv Xi = 1 if i selects its own hat and 0 otherwise.
    → {Xi}, i=1,2,3, …, n : identically distributed.
    
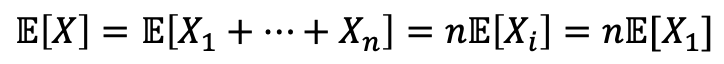
    → 그러면 Expectation은 다음과 같은 식을 만족할 것이고, X1 = 1/n이므로, E[X]=1이 될 것이다.
  2. Are Xis ars independent? If yes, easy to get var(X).
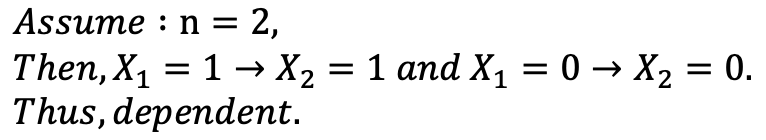    → 다음과 같은 간단한 가정만으로도 Xi들은 dependent하다는 것을 알 수 있다.
    → independent하면 var 계산이 쉬울테지만,,,아니니까 하나 씩 해야된다.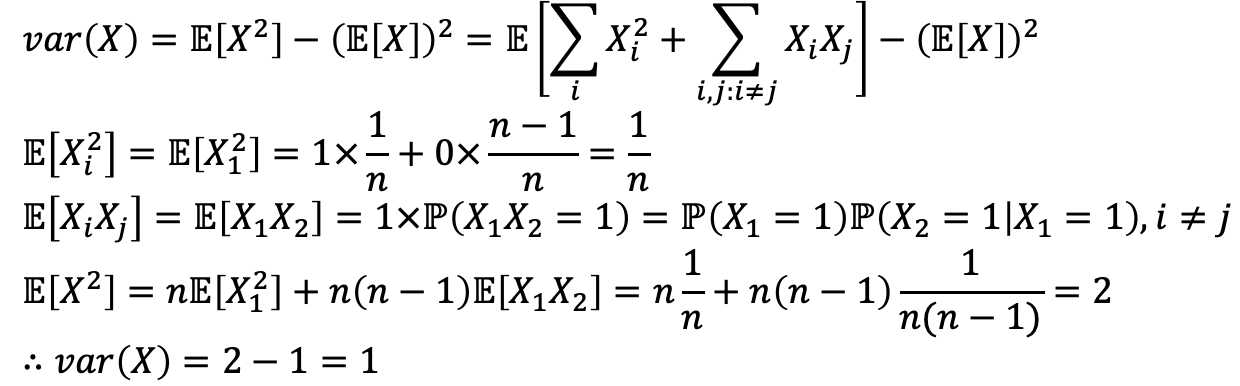
    
    → Xi가 identically distributed이기 때문에 i에 어떤 값이 들어가도 괜찮다는 것을 기억하자.