Random Variables (4)
Random Variables (4)
현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.
Continuous Random Variable and PDF (Probability Density Function)
-
일상에서 많은 RV는 보통 continuous values를 갖고 있음
→ 대표적인 예로, 자동차의 속력🚗 -
All of the concepts and methods for discrete RVs have continuous counterparts.
→ 이를 간단한 그래프와 수식으로 살펴보자.
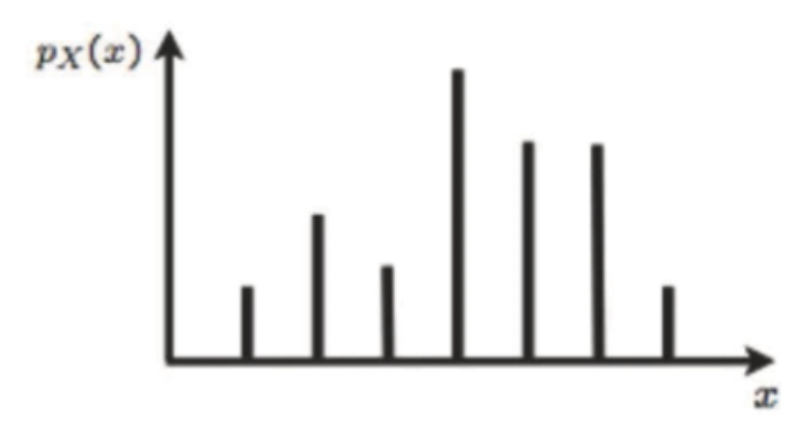
→ 지금까지 봐왔던 discrete RVs이다. 여기서, 두 값(x) 사이의 확률은 어떻게 구할 수 있을까?💩
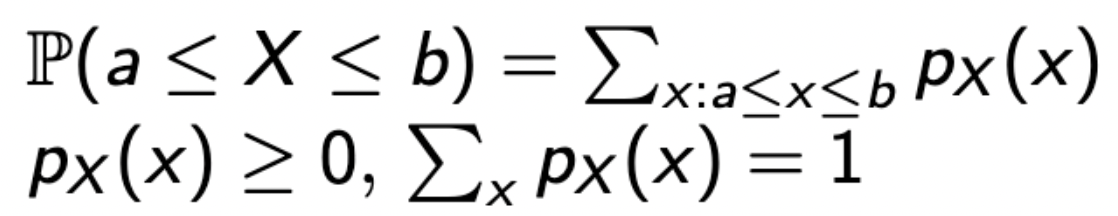
- 간단하게 그 사이의 값을 더하면 된다.
- 물론, 이를 만족하려면 두 번째 조건을 만족해야 한다.
→ 그러면, 이 개념을 continuous로 확장한다면 어떤 개념을 추가하면 될까? 바로, 적분이다.
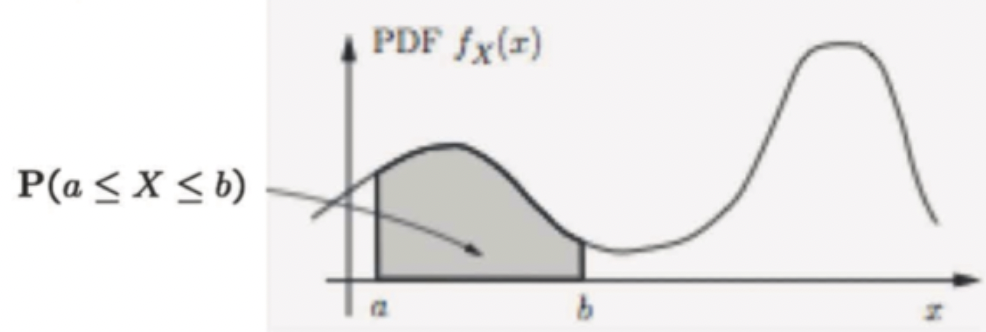
-
Continuous values들의 그래프는 고등학교때부터 봐왔던 꾸불꾸불한 모습을 갖고 있다.
-
그럼 a와 b 사이의 확률은 어떻게 구할까?
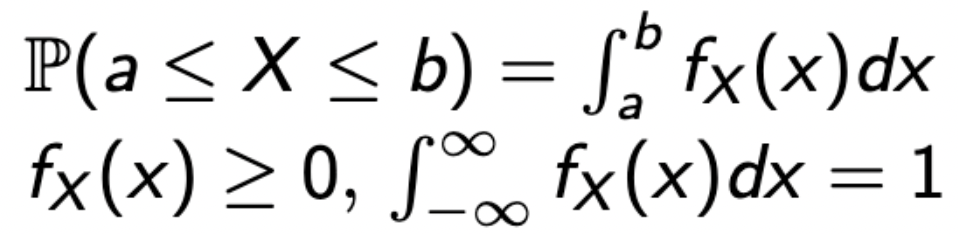
- 간단하게 흔히 알고 있는 적분 공식을 사용하면 된다.
- 이것도 두 번째 조건을 만족해야 한다.
- 이것이 PDF(Probability Density Function)이며, notation이 바뀌었음을 확인하자.
-
PDF의 속성을 살펴보자.
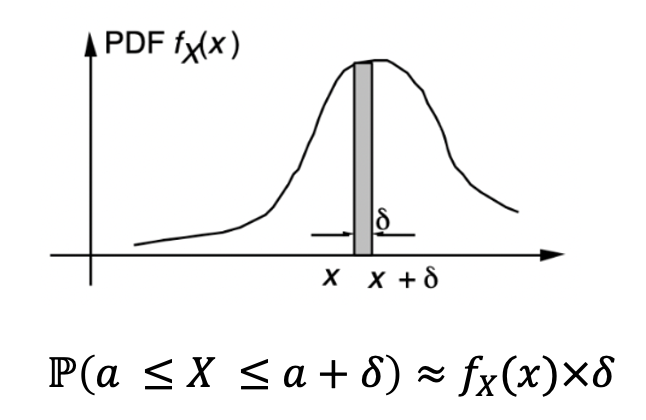
- 지금까지 설명했던 적분의 형태이다. 그러면 우리는 아주 아주 작은 δ를 사용한다면, 특정 값에서의 확률을 비슷하게 구할 수 있다.
- 하지만, ‘특정 값’에서의 확률은 0이 된다. 적분은 넓이니까! 💩
-
자 한번, uniform한 형태에서 PDF 그래프를 그려보고, Expectation과 Variance를 구해보자.
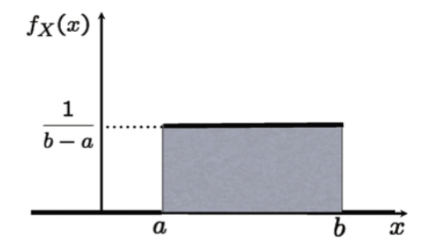 → PDF 그래프는 다음과 같이 그려지고, 총합은 당연히 1이 나온다.
→ PDF 그래프는 다음과 같이 그려지고, 총합은 당연히 1이 나온다.
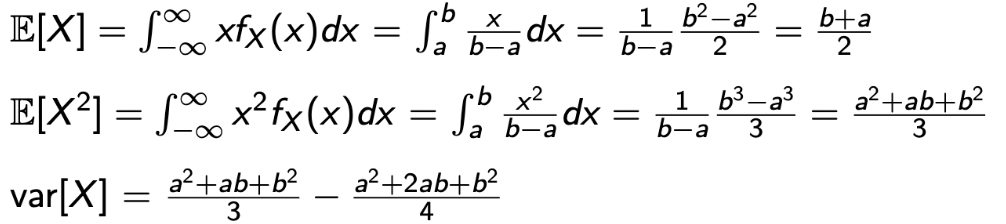
- Expecatation과 Variance는 다음과 같이 쉽게 구해질 수 있다.
- Expecatation과 Variance는 다음과 같이 쉽게 구해질 수 있다.
CDF (Cumulative Distribution Function)
-
그렇다면, 지금까지 배운 PMF와 PDF를 종합할 수식은 없을까?
- Discrete : PMF
- Continuous : PDF
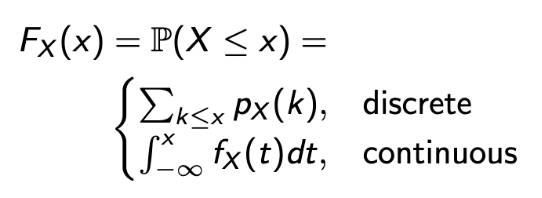
→ 간단하게 표현이 가능하고, 이는 단순히 이전의 값을 모두 더한 것을 의미한다.
→ 그래프로 PMF가 CDF로 변환되는 과정을 살펴보자. 💩
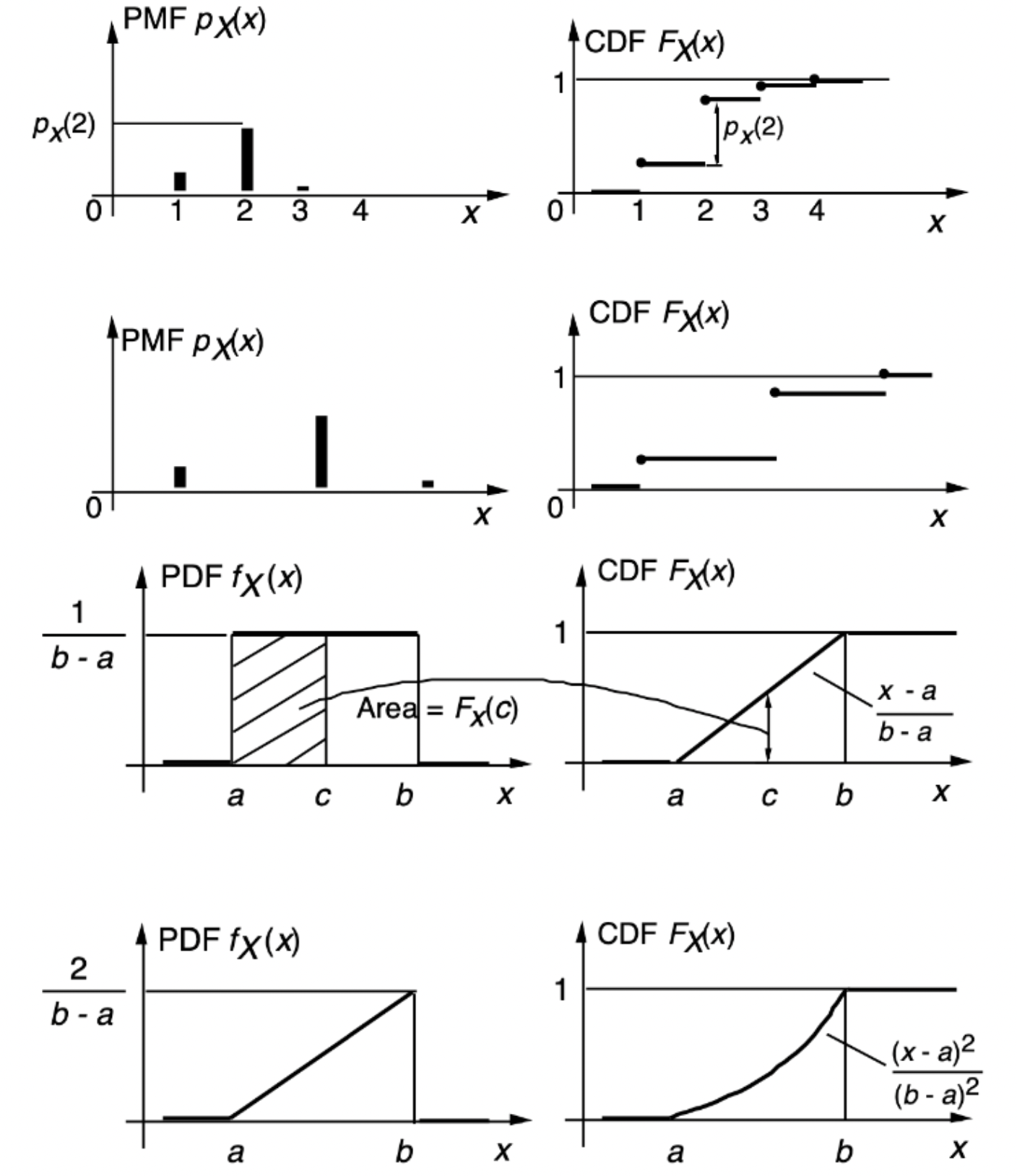
→ 수식과 종합해서 본다면, ‘누적’된 값임을 알 수 있다.
-
이러한 CDF의 속성을 한 번 살펴보자.
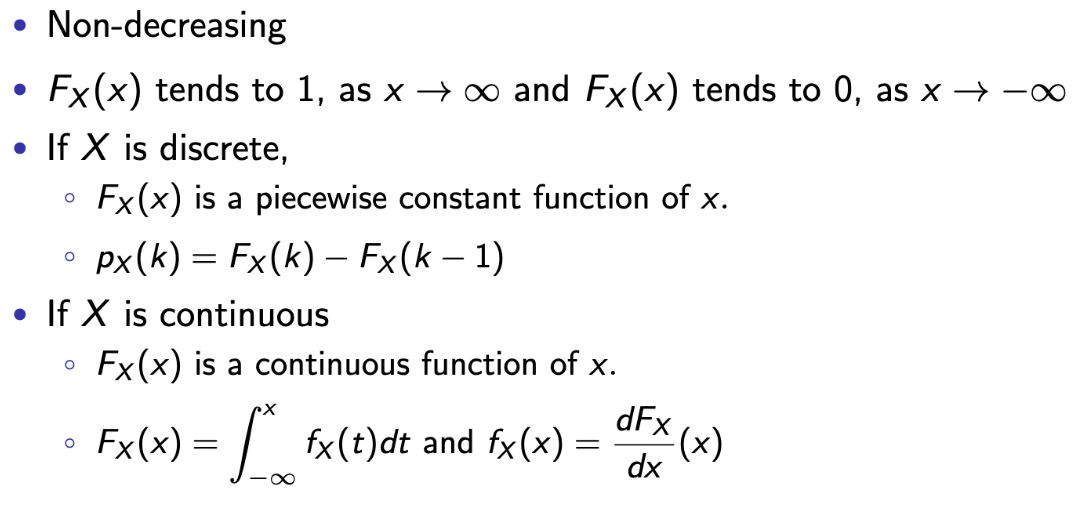
→ 앞서 말한, PMF와 PDF의 속성 덕분에 누적 값은 항상 증가하는 방향이다. (내 카카오 주식은 반대다.)→ 또한, 무한대로 갈 수록 1에 가까워지고 그 반대의 경우에는 0으로 수렴하게 된다.
→ 여기가 중요하다🐯- discrete의 경우에는 CDF는 piecewise constant function(계단 함수)의 형태를 갖게 된다.
→ 그러면 k에서의 확률은 CDF에서 k번째와 k-1번째 값을 빼서 계산이 가능하다. - continuous의 경우에는 PDF와 CDF의 관계성이 나타나게 된다.
→ PDF를 적분해서 얻은 것이 CDF이기 때문에, 미분을 했을 땐 역으로 계산할 수 있다.
- discrete의 경우에는 CDF는 piecewise constant function(계단 함수)의 형태를 갖게 된다.
-
예제를 하나 생각해서 CDF의 이점을 생각해보자.
- 세 번의 시험을 본 뒤 점수를 내고, 네 번째 시험에서의 점수가 앞선 세 점수보다 높을 확률을 구해보자.

- 세 번의 시험을 본 뒤 점수를 내고, 네 번째 시험에서의 점수가 앞선 세 점수보다 높을 확률을 구해보자.
Exponential RV
-
이는 파라미터 λ를 갖는 exponential RV를 의미한다.
-
수식으로 보면 더욱 간단하다.
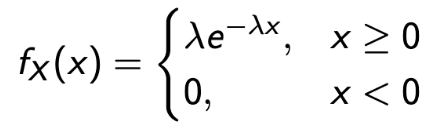
-
λ에 따라 RV는 특성을 다르게 갖게 된다.
→ λ가 크다면 : 급격히 낮아지는 형태의 RV를 갖게 된다.
→ λ가 작다면 : 천천히 낮아지는 형태의 RV를 갖게 된다.
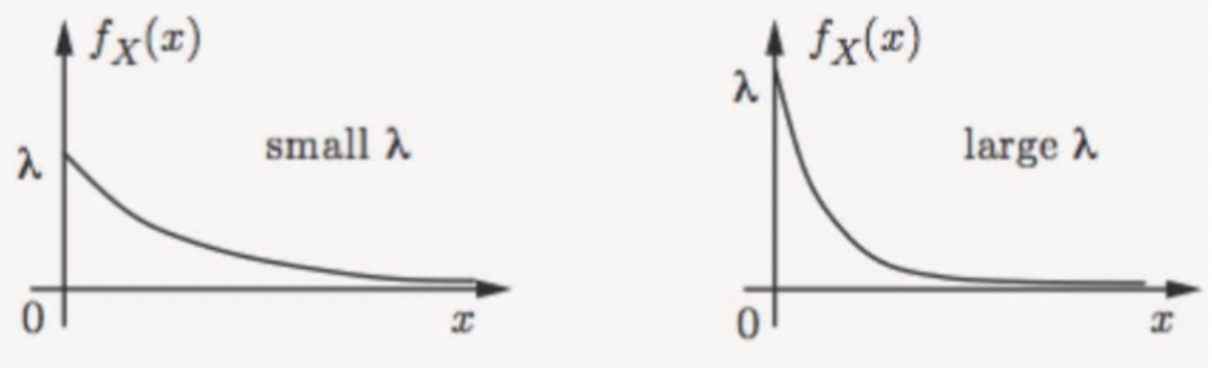
-
그렇다면, Exponential RV를 사용하여 CDF, Expectation, Variance를 구해보자.
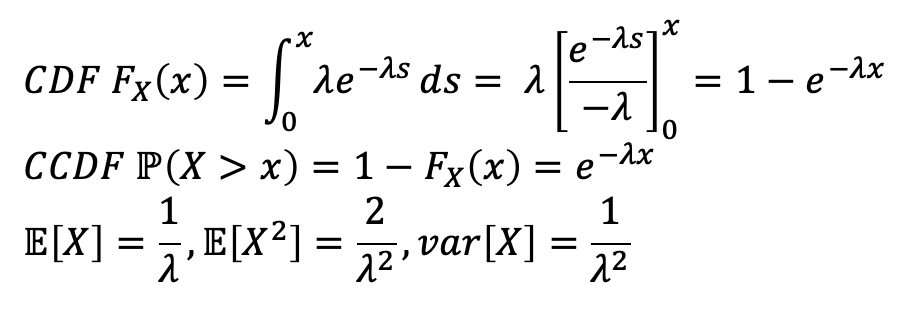
→ CCDF는 Complementary CDF를 의미한다.
→ 이러한 CCDF는 Waiting Time 모델링에 유리하다. 이후 예제에서 이를 다루겠다.
→ Expectation과 Variance를 구하는 방법은 다음과 같다. -
그럼, Waiting time 모델링에서 어떻게 유리한지 예제를 통해 살펴보자.
→ messages arriving at a computer, some equipment breaking down, a light bulb burning out, etc…
→ 근데, 우리는 앞서 이러한 ‘발생 확률’을 예측하는 것을 해보지 않았는가? Geometric→ 이건 또 나중에 살펴보도록 하고, 먼저 예제를 들어보자
- 메테오가 한국에 떨어진다고 한다. 큰일이다.⚠︎
- Time of landing은 Expectation(mean)을 10 days로 갖는 Exponential RV로 모델링 되어있다.
- 그러면, 현재가 자정일 때 첫 날, 6시와 18시 사이에 메테오가 떨어질 확률은 어떻게 될까?
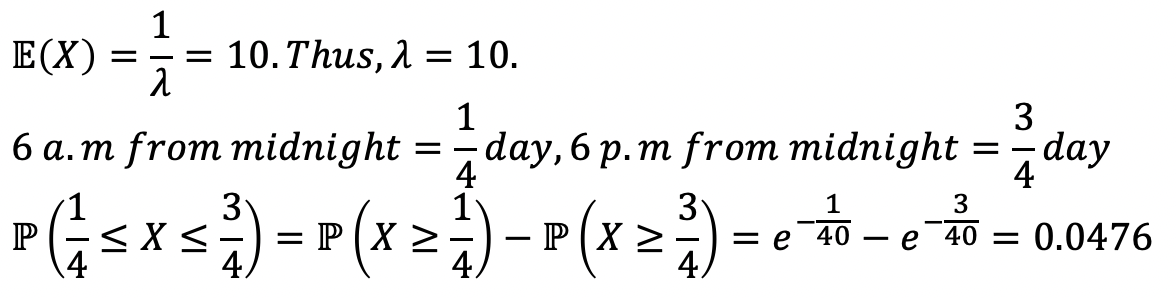
→ CCDF를 사용한다면 이와 같이 쉽게 해결할 수 있다.
-
자, 그럼 뒤로 미뤄뒀던 Geometric과의 차이점을 알아보자.
- 어떤 상점에서 손님의 도착에 대한 정보를 저장하고 있다.
- 30분 동안 들어온 손님의 수를 기록한다. (30분의 window size를 갖는다.)
→ discrete - 손님들이 들어온 정확한 시간을 기록한다.
→ continuous
- 30분 동안 들어온 손님의 수를 기록한다. (30분의 window size를 갖는다.)
-
이 둘의 기록하는 방법(modeling)에서의 차이점은 존재하지만, 두 방법이 ‘틀린 방법’은 아니다.
-
In many cases, continuous case is some type of limit of its corresponding discrete case.
→ 그렇다면, 수학적으로 어떻게 geometric과 exponential이 극한에서 만나는지를 설명할 수 있을까?-
이를 위해 몇 가지 가정을 해보자.
-
SLOT : 단위 시간
-
Continuous system == Discrete system with
→ infinitely many slots whose duration is infinitly small.
→ success probability “p” over one slot decrease to 0 in the limit. -

→ geometric RV인 X_δ^geo를 새롭게 가정하자. -
위에서 정한 geometric RV의 success probability를 P_δ라고 하자.
→ 그러고,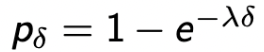 이라고 하면, 얘는 마법같이 앞서 얘기한 Exponential RV의 조건에 모두 부합하게 된다.
이라고 하면, 얘는 마법같이 앞서 얘기한 Exponential RV의 조건에 모두 부합하게 된다.
-
-
가정한 내용을 기반으로, X_δ^geo의 확률을 구해보면,
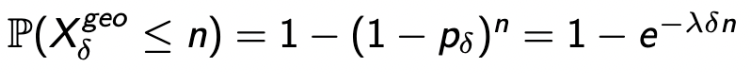
→ Geometric이니까, 그 녀석의 수식이 적용된다.
→ 근데, 얘는 Exponential CDF와 비슷하게 생겼다.-
자, 그래프로 한 번 보자.
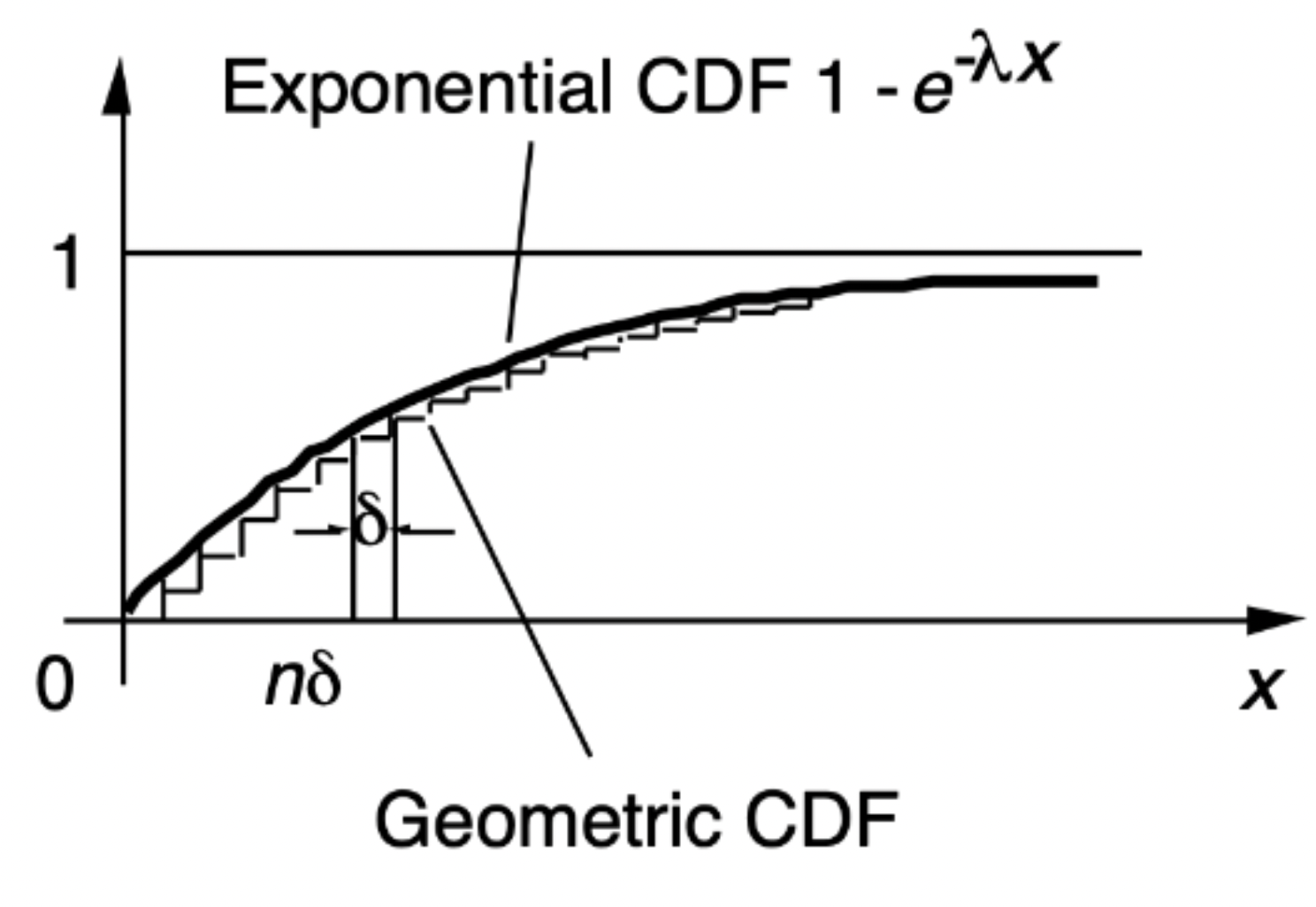
→ δ는 slot의 길이였고, n이 자연수라면, δn은 slot이 n만큼 이어질 때의 위치가 될 것이다.
→ 즉, nδ는 그래프에서 보이듯 x값이라 할 수 있다. -
이 내용을 정리한다면 다음과 같다.
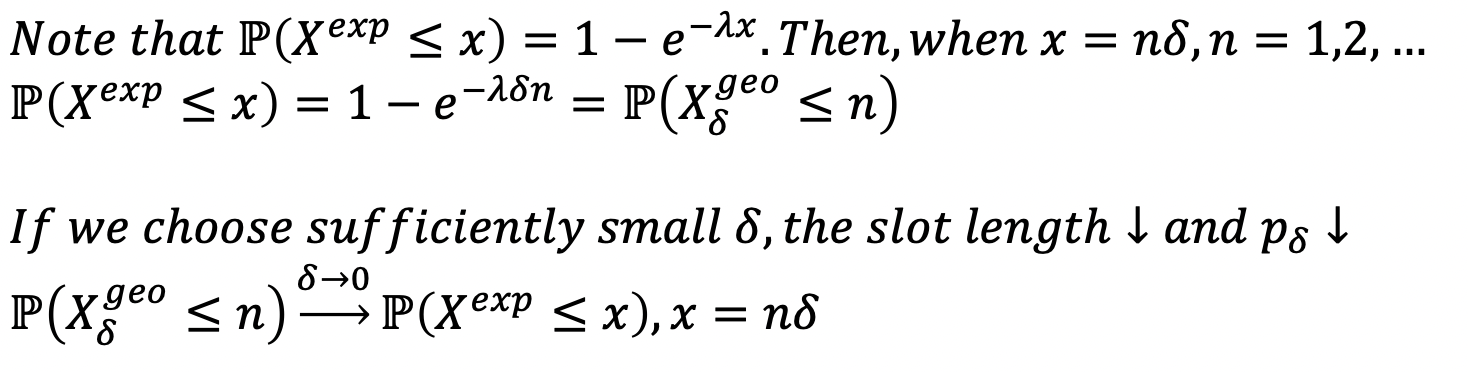
-
-
- 어떤 상점에서 손님의 도착에 대한 정보를 저장하고 있다.