Random Variables (5)
Random Variables (5)
현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.
Gaussian (Normal) RVs
| Standard Normal | General Normal |
|---|---|
Notation : 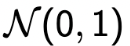 PDF : 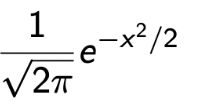 Expectation And Variance 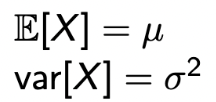 |
Notation : 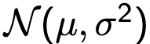 PDF : 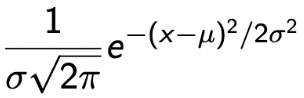 Expectation And Variance 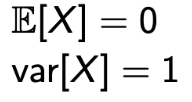 |
→ Expectation은 μ를 중심으로 symmetric하다는 것을 알 수 있다.
→ 또한, PDF의 속성인 Normalization은 다음과 같은 수식으로 증명이 된다. (적분 수업이 아니여서 전개 과정은 없다.💩)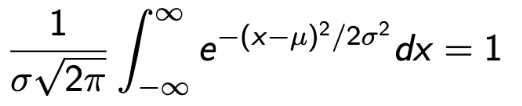
→ Variance는 다음과 같은 수식으로 증명이 되고, 이는 E[(X-μ)^2]과 같다.
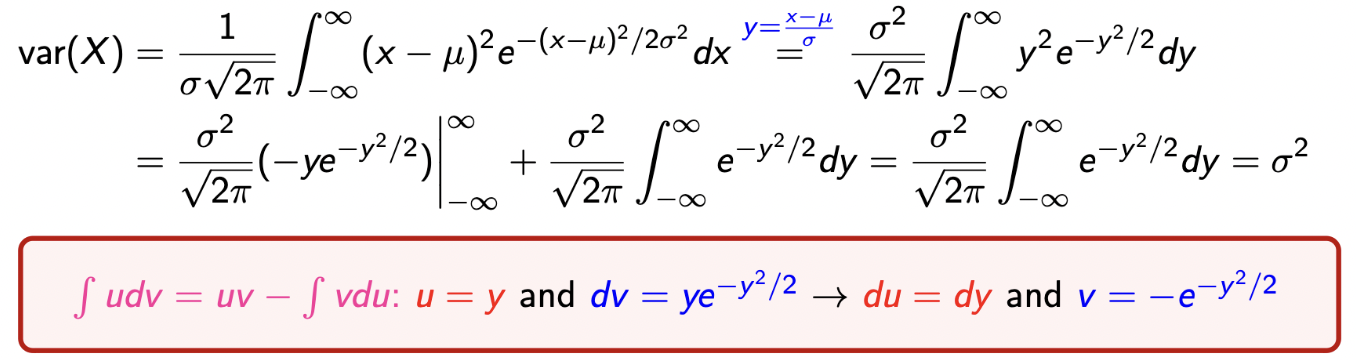
→ 마지막 부분에서 Normalization property가 적용됨을 확인하자.
-
Normal RV의 특이한 속성을 알아보자.

→ X가 Normal일 때, 이를 통해 만들어진 RV Y또한 Normal함을 알 수 있다.→ Expectation과 Variance는 다음과 같이 쉽게 구해질 수 있다.
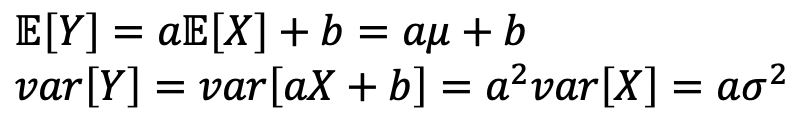
→ Thus, every normal RV can be STANDARDIZED.→
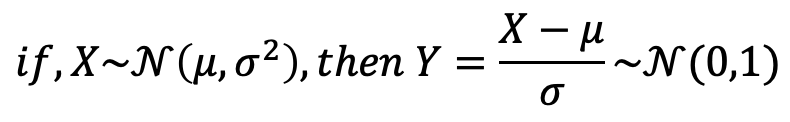
-
Standardized된다는 것이 어떠한 의미를 가질까?
-
모든 normal RV의 CDF를 특정한 표(table, Φ)를 사용하여 쉽게 구할 수 있다.
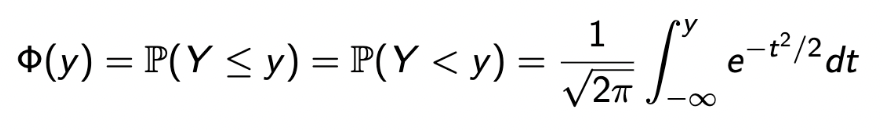
-
이걸 적용한 예제를 하나 살펴보자.
-
매년 강설량 X를 N(60, 20^2)으로 모델링 했다고 하자. 그럼, 최소 80 inches일 확률은 몇인가?
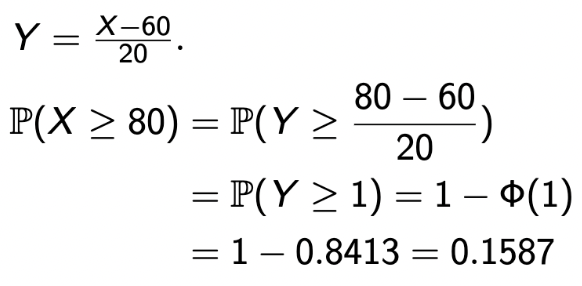
→ 구하려는 X를 Y로 변환함으로써 Standardized를 하고, 테이블을 통해 쉽게 구할 수 있는 것을 확인할 수 있다.
-
-
-
Normal RVs : Why Important?
- Central limit theorem (중심 극한 정리)
→ 모집단이 Normal을 이룬다고 할 때, 이 모집단으로부터 추출된 표본의 크기가 충분히 크다면 표본 평균들이 이루는 분포는 정규분포에 근접한다.- One of the most remarkable findings in the probability theory
- Sum of any random variables ≈ Normal random variables
- Modeling aggregate noise with many small, independent noise term
- Convenient analytical properties, allowing closed forms in many cases
- Highly popular in communication and machine learning ares
- Central limit theorem (중심 극한 정리)
Continuous : Joint PDF and CDF (1)
- 다음과 같은 조건을 만족한다면, 두 개의 continuous RV는 jointly continuous라고 말할 수 있다.
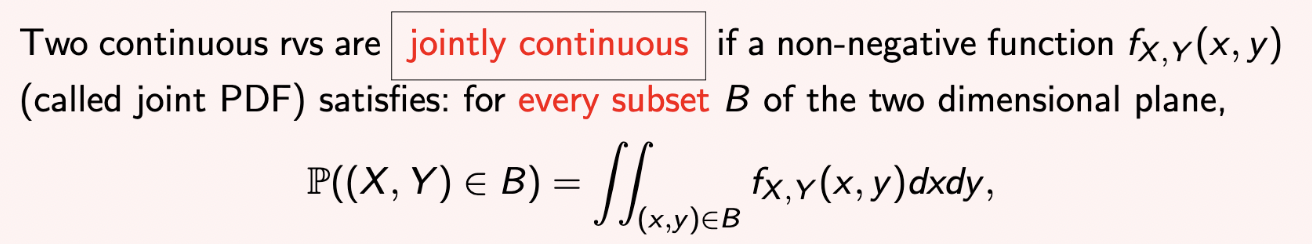
- B는 subset이고, two dimensional plane은 쉽게 생각하면 바둑판이라고 생각할 수있다.
→ B = { (x, y) | a <= x <= b, c<= y <=d } - The Marginal PDFs of X and Y are from the joint PDF as :
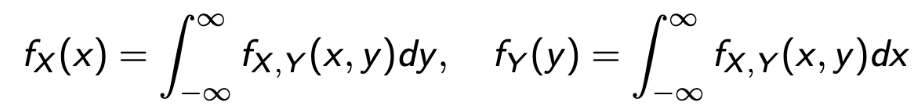
- The Joint CDF is defined by F_(X, Y)(x,y) = P(X <= x, Y <= y) and determines the Joint CDF as :
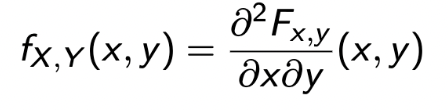
→ CDF와 PDF의 연관성은 미분과 적분이였음을 기억하자💩 - A function g(X, Y) of X and Y defines a new random variable, and
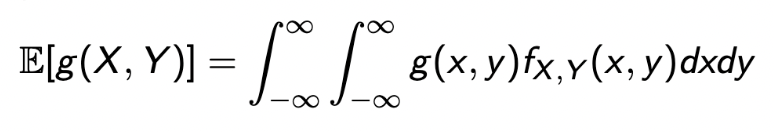
-
Event가 주어졌을 때, PDF를 구해보자. 즉, Conditional PDF, given an event A를 생각해보자.
✣ 여기서 사용하는 A 는 event를 의미하고, B와 C는 subset을 의미한다.
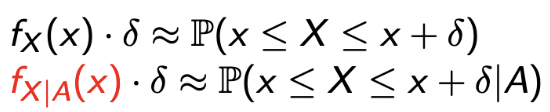
- PDF의 정의를 통해서 첫 번째 줄이 어떻게 나오는지 알 수 있고, conditional PDF는 두 번째 줄과 같이 나온다는 것을 이해하자.
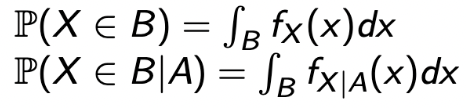
- 어떠한 subset 안에서의 PDF는 첫 번째 줄과 같이 나올 것이고, 여기서 subset에 이벤트가 주어졌을 때, 두 번째 줄과 같이 나온다.
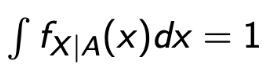
- 그리고, 당연히 event 내에서의 PDF는 1이 된다. 💩
- PDF의 정의를 통해서 첫 번째 줄이 어떻게 나오는지 알 수 있고, conditional PDF는 두 번째 줄과 같이 나온다는 것을 이해하자.
-
Event가 아닌, subset 에 포함된다는 event가 주어졌을 때, conditional PDF는 어떻게 될까?
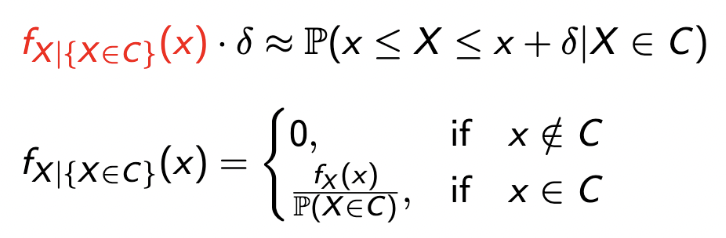
💩 이렇게 된다~!
-
추가로, Conditional Expectation을 구해보자.
→ 먼저, 그림을 통해 일반 PDF를 통해 Conditional PDF를 구하는 방법을 확인해 보자.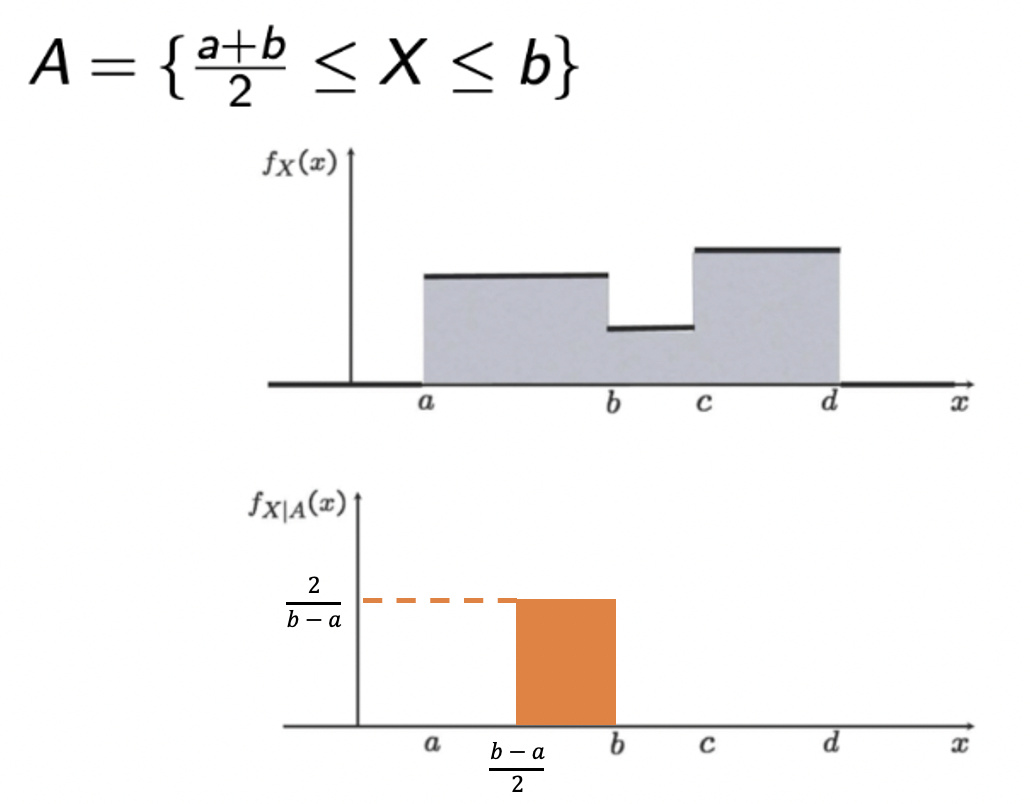
→ Conditional로 떨어진 부분의 넓이는 1이 되어야 하기 때문에 높이가 2/(b-a)가 됨을 확인합시다~🐯-
이렇게 되면, Conditional Expectation은 쉽게 구해질 수 있고,
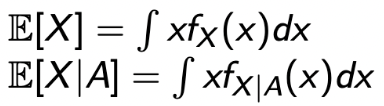
-
rv X를 통해 만들어지는 새로운 rv g(X)에 대해서도 확장해서 적용할 수 있다.
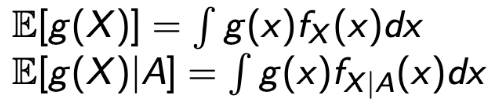
-
그럼, 그림에서 나온 Conditional PDF의 Expectation은 어떻게 구할 수 있을까?
→ 위 공식을 사용하면 쉽게 구할 수 있다.
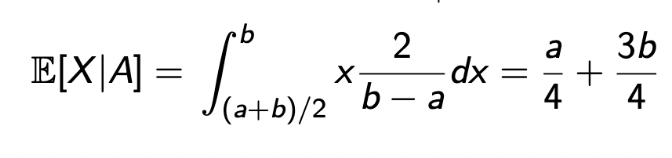
-
-
Example : Train Arrival
-
예제에 들어가기 앞서, 이전에 배웠던 두 가지에 대해 다시 살펴보자
-
Exponential RV : Memoryless
-
Exponential RV는 geometric RV의 continuous counterpart이다.
-
그래서, geometric의 memoryless를 exponential도 가질 것이라 기대할 수 있다.

-
Exponential RV의 CCDF를 사용하고, CCDF P(X > x) = e^(-λx)라 하면,
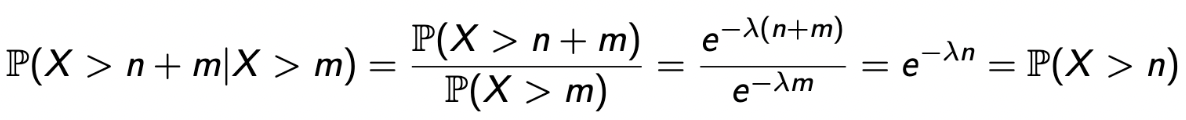
→ 이니까, 나의 기대를 충족시켰다.
-
-
Total Probability / Expectation Theorem
Discrete Case Continuous Case Total Probability Theorem 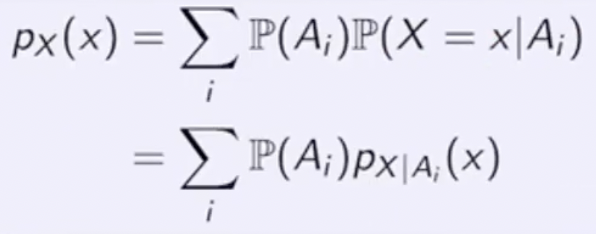
Total Expectation Theorem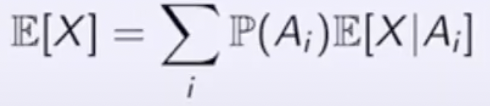
Total Probability Theorem 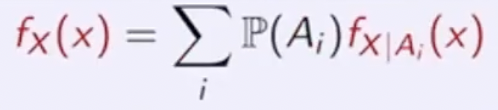
Total Expectation Theorem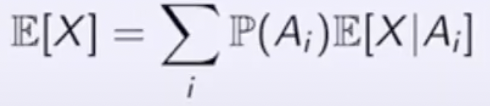
-
예제 설명 시작.
- 어떤 기차🚃는 15분에 한 번 씩 도착을 한다. (every quater hour, 0min - 15min - 30min - 45min - 60min)
- 나는 7:10~7:30에 도착할 것이라 예상되고, 10분에서 30분 사이의 확률은 Uniform하다.
- 기차가 도착할 때까지 기다려야하는 시간의 PDF는 어떻게 계산해야 할까?
- X : your arrival time, Y : waiting time
-
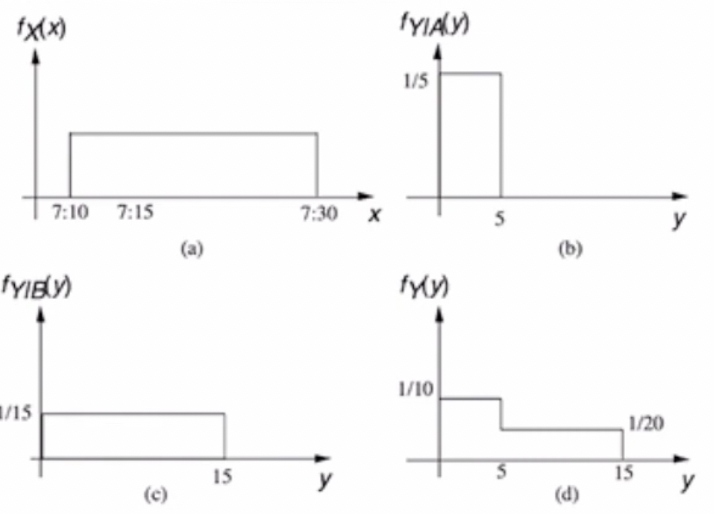
먼저, X에 따라 waiting time이 달라지니까 두 개의 유형으로 분류를 하자.
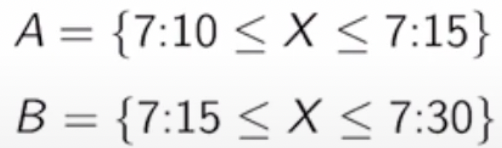
-
그러면, Y에게 A 또는 B 이벤트가 발생했을 때의 condition을 부여하고, Total Probability Theorem을 적용하면 구할 수 있다. (물론, Continuous이다💩)
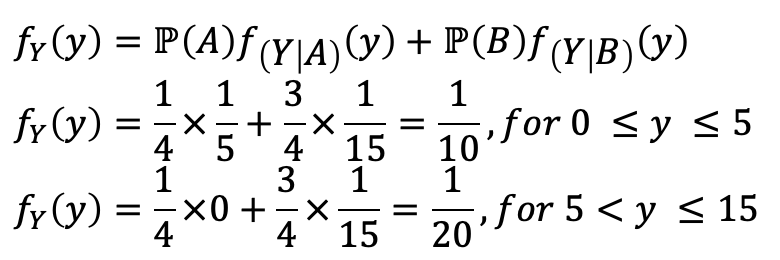
- 15분에 도착했을 때, 30분 기차를 타야한다!!
- 15분에 도착했을 때, 30분 기차를 타야한다!!
-
Conditional PDF given a RV
- 이전에 했던 내용의 반복이고, 단순히 PDF로 치환만 하면 된다.
- 이건 첨부를 그냥 하겠다…이전 내용을 다시 복습해야할 필요성도 많이 느껴진다.😢

-
이를 활용한 예제를 하나 살펴보자.
-
Stick-breaking
-
길이가 l인 막대를 반으로 쪼개버렸다..
-
두개로 나뉘어진 막대 중 첫번째 막대는 길이가 Y이고, 이 막대를 다시 쪼갰다.
-
막대는 두 개로 쪼개졌고, 이 중 하나의 길이가 X이다.
-
Y와 X는 uniform한 형태로 나타나게 되며, Y ~ U[0, l]이고 X ~ U[0, Y]이다. (U는 Uniform을 의미한다.) 즉, Continuous하다.
first break at Y ~ U[0, l]
second break at X ~ U[0, Y]
- Joint PDF f_(X, Y) (x, y)를 구해보자.
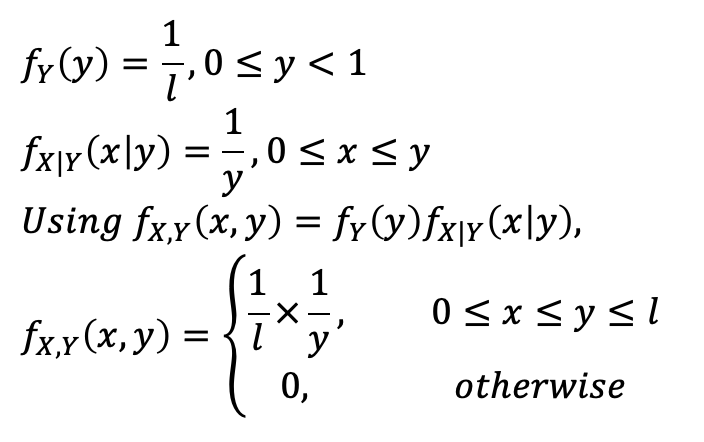
💩 앞서 내가 그림만 뚱땅 올린 내용을 통해서 쉽게 구해질 수 있다. discrete에서 continuous로 생각만 하면 된다! - Marginal PDF f_X(x)를 구해보자.
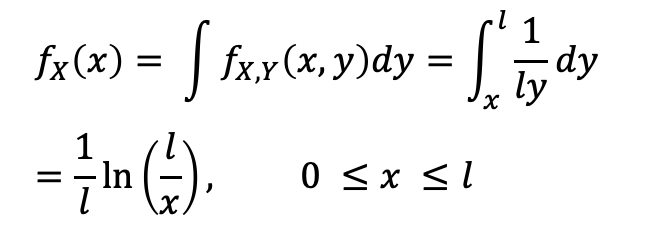
- Evaluate E(X), using f_X(x)
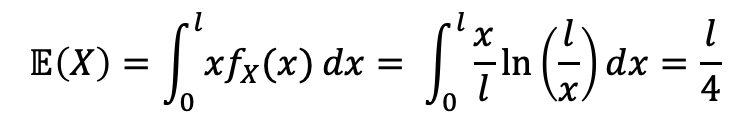
- Evaluate E(X), using X=Y*(X/Y)
→ if X ㅛ X/Y, it becomes easy, but true?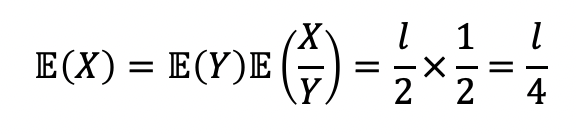
→ X 와 Y가 왜 독립적인지는 이해가 잘 가지 않는다… 수업에서는 처음 막대가 어떻게 잘리든 X의 분포가 달라지지 않기 때문이라고 한다.(uniform하기 때문) - Evaluate E(X), using TET
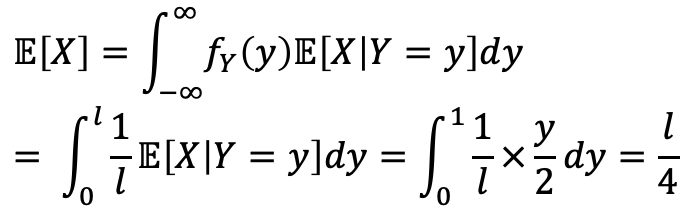
- Joint PDF f_(X, Y) (x, y)를 구해보자.
-
Expectation을 구하는 방식은 여러 개가 있음을 또한 확인할 수 있다.
-
-
-
Bayes Rule For Continuous
-
이전에 배웠던 discrete에서의 Bayes Rule은 원인(X)과 결과(Y)가 주어지고, 원인에 대한 확률(P(X)) 그리고 원인이 있을 때 이에 따른 결과가 나올 확률(P(Y | X))을 알고 있을 때, P(X | Y)를 구하는 문제였다.
-
이는 수식으로 다음과 같이 정의가 되었다.
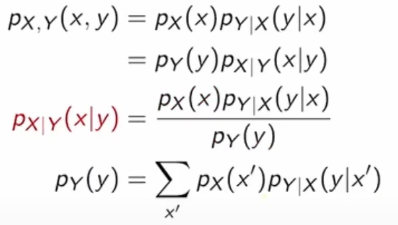
-
그럼, Continuous에선? 간단하다. 지금까지 했던 것과 같이 PDF로 바꿔치기만 하면 된다!💩
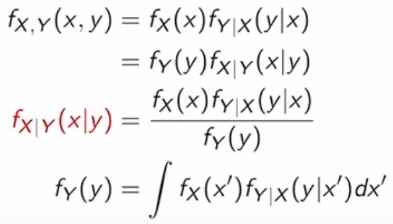
-
예제를 하나 살펴보자!
-
A light bulb Y ~ exp(λ). However, there are some quality control problems. So, the parameter λ of Y is actually a random variable, denoted by Λ, which is Λ ~ U[1, 3/2]. We test a light bulb and recored its lifetime.
-
Q. What can we say about the underlying parameter λ? In other words, what is f_(Λ | Y)(λ | y)?
→ y가 변함에 따라, 전구의 수명이 달라지게 될 것이고, 람다를 통해 정의되는 Y값에서 역으로 y의 변화에 따른 람다 값을 추정하는 것 -
Then, the inference about the parameter given the lifetime of a light bulb is :
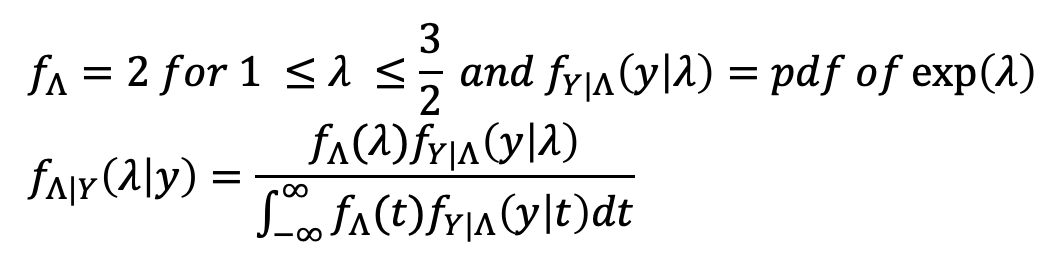
-
-
Using Bayes Rule for Parameter Learning

- Example.
- Light bulb’s lifetime Y ~ exp(λ). Given the lifetime y, the modified belief about λ ?
- Remeo and Juliet start dating, but Romeo will be late by a random variable Y ~ U[0, θ]. Given the time of being late y, the modified belief about θ?
- Example.
-
Bayes Rule for Mixed Case
-
K : discrete , Y : Continuous
A. Inference of K given Y B. Inference of Y given K 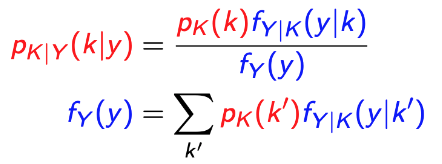
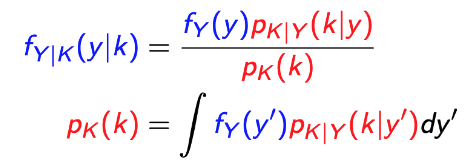
-
A에서, f_(Y|K)(y|k) = f_(Y|A)(y), where A = {K = k}
-
B에서, p_(K|Y)(k|y)가 과연 맞는 표현일까? 아래 수식을 보면 뭔가 이상하다…
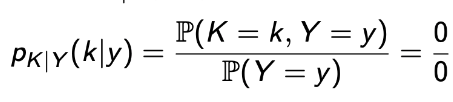
→ 그럼 이 친구를 어떻게 정의해야할까? P(Y=y) = 0이니까, 극한을 사용하자.-
For small δ (in other words, taking the limit as δ → 0)
-
Let A = {K = k}
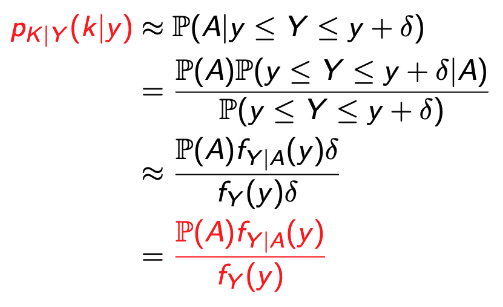
-
-
예제를 통해, 이를 이해해보자.
- 통신이다!
- 신호(K)를 -1과 1로 쏜다. 근데, 잡음이 Gaussian Noise로 끼고 있어 도착한 신호(Y)는 뭔가 다르다.
- K : -1, +1, original signal, equally likely. p_k(1) = 1/2, p_k(-1) = 1/2.
- Y : measured signal with Gaussian Noise, Y = K + W, W ~ N(0, 1) (N : normal)
- 자 그러면, 직관으로 확인해보자.
- 내가 신호 0.7을 받았다. 원 신호는 무엇일까?
→ 양수니까 원래 1로 보냈겠지. - 내가 신호 -0.2를 받았다. 원 신호는 무엇일까?
→ 음수니까 원래 -1로 보냈겠지.
- 내가 신호 0.7을 받았다. 원 신호는 무엇일까?
- 근데 이건 단순히 직관이다. 수학적으로 어떻게 정의를 해서 내 직관이 맞음을 증명할 수 있을까?
- Y | {K = 1} ~ N(1, 1) and Y | {K = -1} ~ N(-1, 1).
→ W가 Normal하니 linear transformation특성때문에 Y도 Normal함을 알 수 있다.
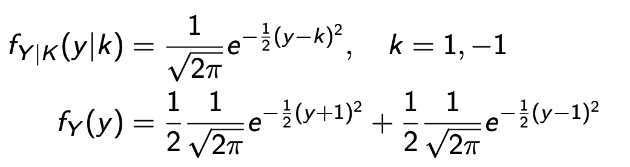
- 이를 통해, 결과(y)에 대한 확률과 원인이 있을 때 결과가 나올 확률을 구할 수 있게 되었다. 그럼 뭐? Bayes Rule💩
- 확률 수업이니 자세한 대수적 계산을 집어 치우고. 최종적으로 다음과 같은 결과가 나온다.
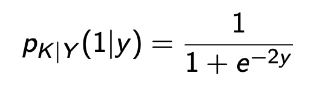
- 얘를 y에 대한 그래프로 그려본다면
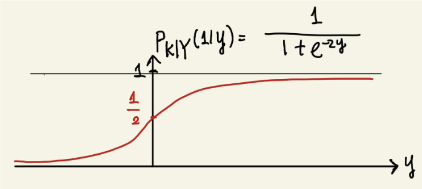
- 이렇게 나올 것이고, y가 양의 무한대로 가게 된다면 확률은 1이 나올 것이다.
→ 그리고 우리의 직관과 같이 양수일 때, 1/2 이상의 확률을 갖게 된다.
→ 이는 -1일 때도 비슷한 양상의 그래프가 나오며 우리의 직관과 같은 결과를 내게 된다.
- Y | {K = 1} ~ N(1, 1) and Y | {K = -1} ~ N(-1, 1).
-
또 다른 예제도 살펴보자.
-
평면에 서로 수평을 이루는 많은 선들이 존재한다. 그리고 이들은 각 d만큼 거리가 떨어져있다.
-
이 평면에 우리는 길이가 l인 바늘을 던진다. (l < d)
-
Q. What is the probability that the needle will intersect one of the lines?
-
간단하게 생각해보자.
- 바늘이 두 선을 교차할 수는 없다. l < d니까.
- 그럼 언제 교차를 하고 언제 하지 않을까?
→ 두 개의 랜덤 변수를 만들어 보자.
-
R1. How far is the needle from the nearest parallel line? → X : vertival distance from the midpoint of the needle to the nearest of the parallel lines.
-
R2. How does the needle meet the nearest parallel line? → Θ : acute angle formed by the axis of the needle and the parallel lines.
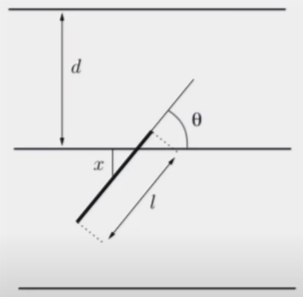
-
이 두 개가 적절한 조합을 가질 때, 바늘은 선을 교차할 것이다.
-
자, 그러면 언제 교차할까?
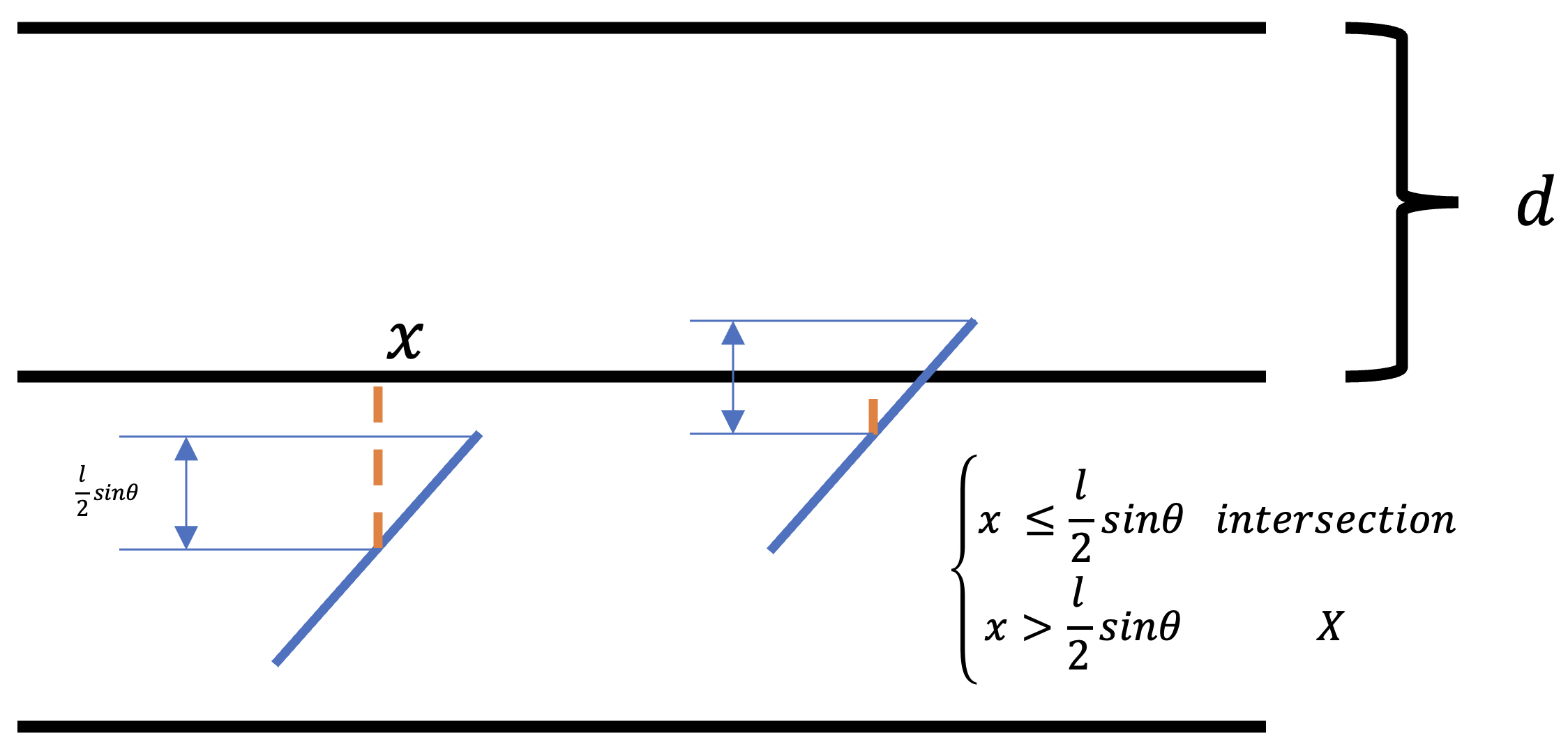
-
그런 다음, joint PDF를 구한 뒤 최종적으로 확률을 구해보자.
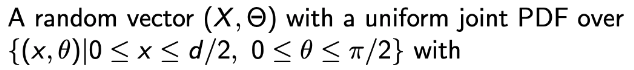
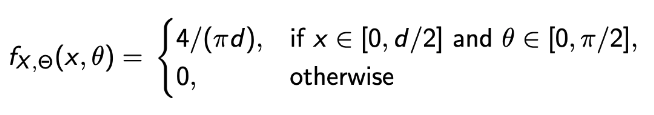
→ f_X 는 2/d이고 f_θ는 2/pi이다. 그리고 둘은 독립이기 때문에 joint PDF는 두 개의 곱으로 나타낼 수 있다. -
조건도 찾았으니 최종적으로 확률을 구해보면.
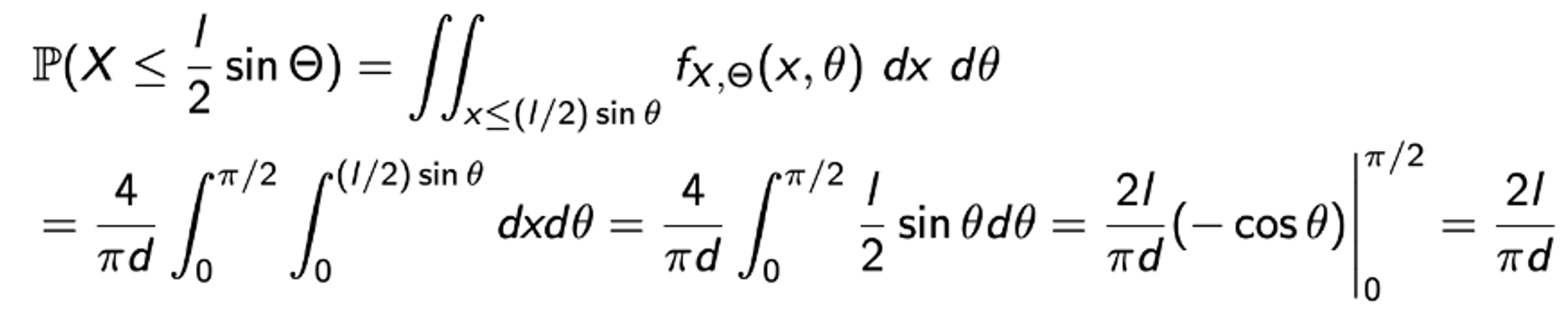
-
-