Random Variables (6)
Radnom Variable (6)
현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.
Derived Distribution: Y = g(X)
-
Given the PDF of X, What is the PDF of Y = g(X) 에 관한 문제이다.
→ g(X) 는 Y = X, Y = X + 1, Y = X^2 등 여러 경우가 있다. -
그럼 어떨 때 쉽고 어떨 때 어려울까?
-
Easy Case
-
Discrete
- 간단하게 case-by-case 로 생각하면 된다.
- 예시를 통해 한 번 알아보자.
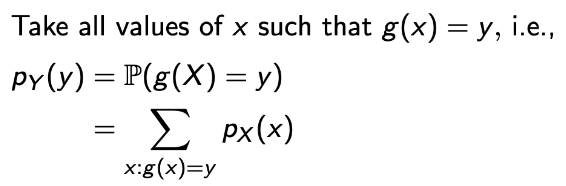
→ 어떤 함수 g로 인해서 Y = g(X) 일 때, Y의 확률 p_Y(y) = P(g(X) = y)일 것이고 이는 y에 값에 따른 x의 값을 모두 합해주면 된다.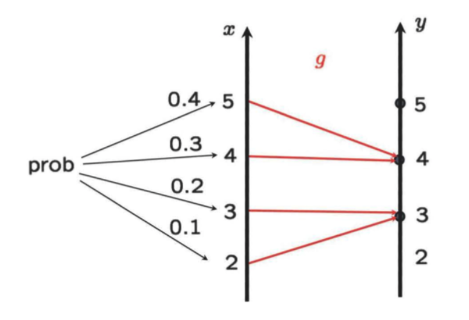
→ g(X)의 동작 과정이 다음과 같을 때, y값은 3과 4일 것이고, 앞서 말한 것과 같이 case-by-case로 생각한다면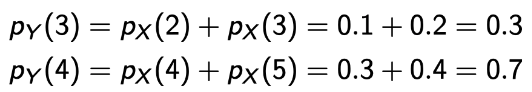
→ 확률은 다음과 같이 구할 수 있다.💩
-
Linear : Y = aX + b, a != 0, X : Continuous
-
a의 값이 양수인지 음수인지를 통해 쉽게 계산을 할 수 있다.
-
a > 0
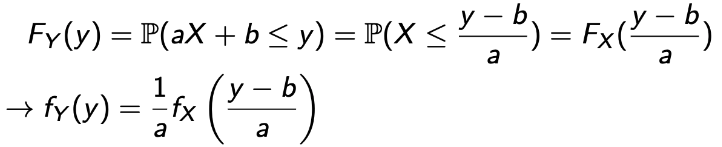 )
) -
a < 0
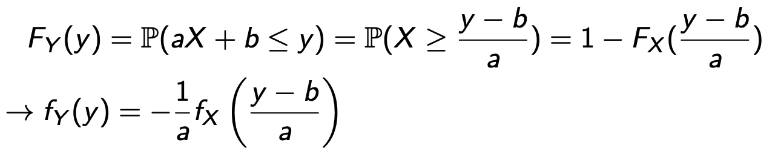 )
) -
그럼 이걸 합쳐보자.
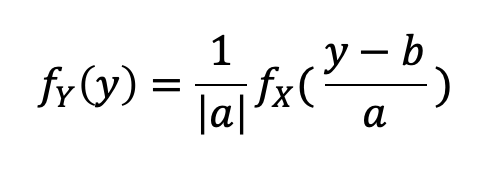
→ a는 0이 될 수 없기에 가능하다.
-
-
-
Linear : Y = aX + b, when X is exponential
- 앞서 구한 방식으로 쉽게 구해질 수 있다.
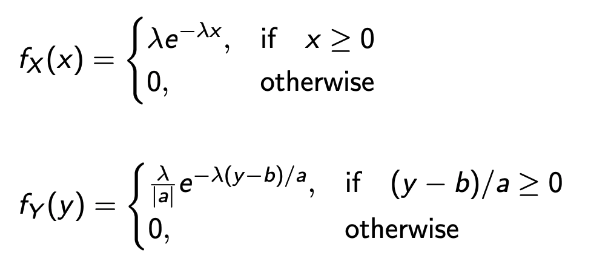
→ 그렇다면, Y 또한 Exponential일까?
→ 일반적으로 그렇지 않고, b = 0 and a >0일 때, Y는 λ/a를 파라미터로 갖는 Exponential RV가 된다.
- 앞서 구한 방식으로 쉽게 구해질 수 있다.
-
Linear : Y = aX + b, when X is normal
- Normal을 베웠을 때, 우리(나)는 Linear transform은 normality를 보존한다는 것을 배웠다.

- 근데, 증명은 안했다. 이제 해보자.
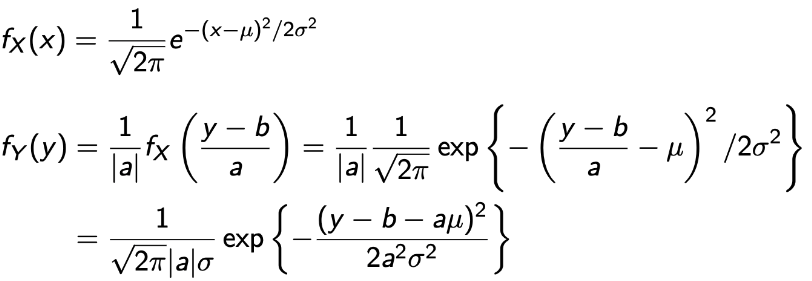
→ 최종적으로 나온 값에서 fX와 fY를 비교해보면, μ자리가 (b+aμ)로 σ는 aσ로 바뀐 것을 보면 된다.💩
→ 그럼 X를 Linear Transform한 Y의 결과는 N(aμ+b, (aσ)^2)이 된다!
- Normal을 베웠을 때, 우리(나)는 Linear transform은 normality를 보존한다는 것을 배웠다.
-
-
Sometimes Easy and Sometimes Difficult Case
-
Y = g(X), X : Continuous
-
말 그대로 쉽기도하고 어렵기도 하다. 하지만 일반적인 원리가 있으니 이 것을 알아보자.
- Step : Find the CDF of Y :
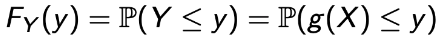
- Step : Differentiate :
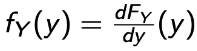
- Step : Find the CDF of Y :
-
예제 몇 개를 보면서 이 원리를 적용해보자.
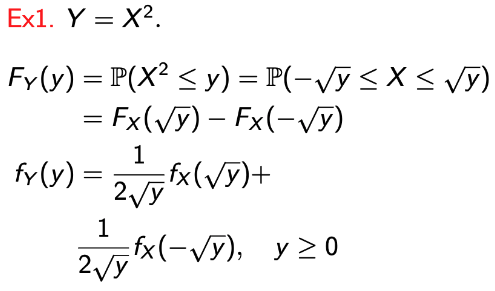
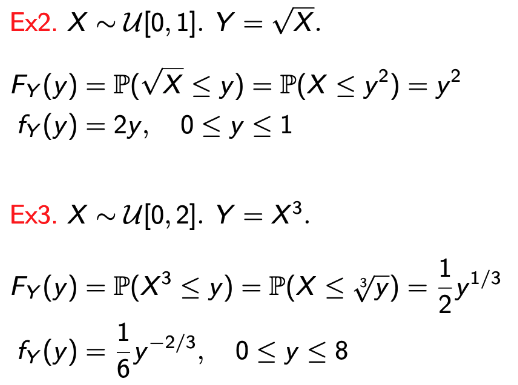
→ g(X)에 따라, Y의 범위가 한정됨을 확인하자.
-
-
-
Derived Distribution: Z = g(X, Y)
-
앞서 배운 원리를 사용하면 된다. 예제를 보자!
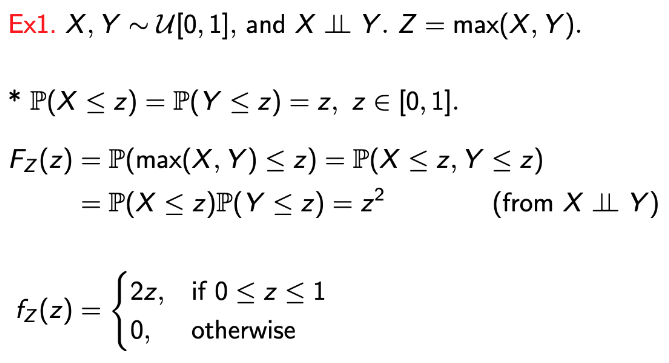
→ X와 Y가 uniform하기 때문에, P(X <= z) = P(Y <= z) = z임은 당연하다.
→ 또한, Z = max(X, Y)일 때는 P(X <= z) and P(Y <= z)이고, 이는 P(X <= z, Y <=z) = P(X <= z)P(Y <= z)이다.
→ 독립이니까!!!!!! -
다음 예제를 살펴보자.

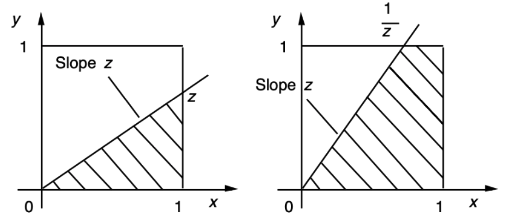
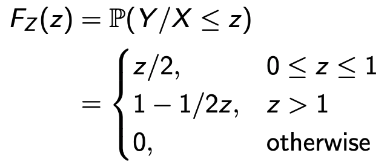
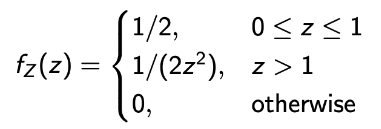
💩 Sometimes, the problem is tricky, which requires careful case-by-case handling!!
Derived distribution of Z = X + Y
Function of multiple RVs
- Z = X + Y, X ㅛ Y (1)
-
Sum of two independent RVs
-
매우 기본적인 예시이지만 사용되는 경우가 매우 많다.
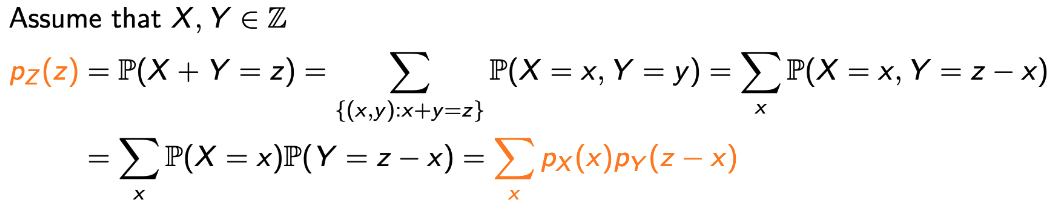
→ pZ(z)는 the PMFs of X and Y의 Convolution이라고 할 수 있고,
→ Convolution은 두 개의 인풋(pX, pY)이 마지막 항 이라는 함수를 통해 pZ가 됨을 의미한다.
→ 여기서 중요한 점은, 이 Convolution이 무엇을 의미하는지이다. 이제 알아보자.
- Z = X + Y, X ㅛ Y (2)
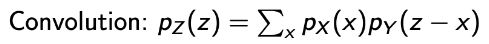
-
Interpretation for a given z :
- Horizontally Flip the PMF of Y → pY(-x)
- Put it underneath the PMF of X
- Right-shift the flipped PMF by z → pY(-x+z)
- Do convolution!
-
실제 예제를 통해 확인해보자.
-
pX와 pY가 다음과 같이 주어졌다.
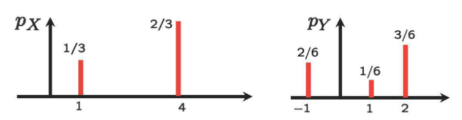
-
Horizontally Flip! And 2. Put it underneath the PMF of X
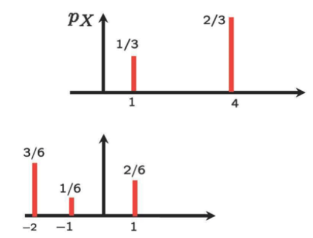
- Right-shift the flipped PMF by z(=3)
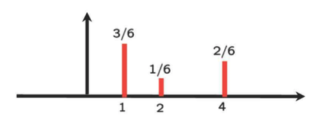
- Do convolution!
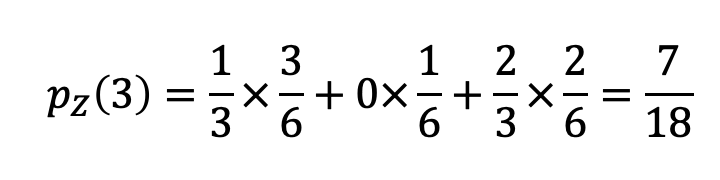
→ 이 과정을 원하는 모든 z에 대해서 수행하면 된다.
-
-
- Y = X + Y, X ㅛ Y, Continuous
- Same logic as the discrete case.
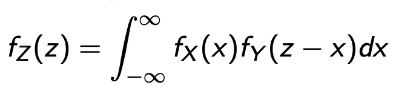
- 그림으로 보면 더 쉽게 이해가 간다. 그리고 계산 순서도 같다! 단지, 넓이를 구할 뿐!
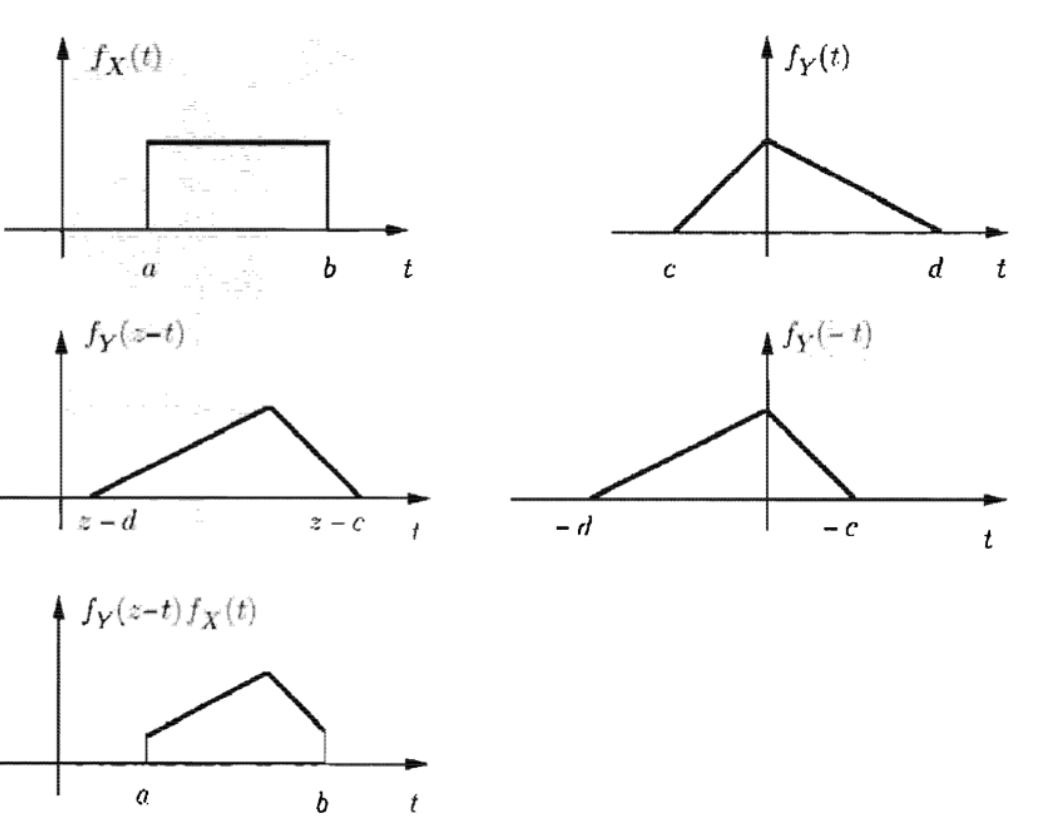
- 예제를 보자~
- X와 Y가 U[0, 1]이라고 하고, X ㅛ Y라고 헤보자.
- 그럼, the PDF of Z = X + Y는 어떠한 형태를 보일까?
- 쉽게 생각해보자. 💩
- Flip : Y는 0~1 값을 가졌으니, -1 ~ 0의 값을 갖게 된다.
- Put under X : 처음에는 겹치는 부분이 하나도 없을 것이다.
- PDF of Z는 0의 값을 가질 것이다.
- 조금씩 옮기다보면 점점 겹치는 영역이 많아지고
- 어느 순간 완전히 겹쳤다가 점점 겹치는 영역이 줄어들어 최종적으로는 완전히 벗어날 것이다.
- 그래서 형태는 다음과 같다.

- Z = X + Y, X ㅛ Y, Normal (1)
- 매우 특별하고 유용한 case.
- 두 개의 Normal RVs의 합(Z)은 다음과 같이 나타낼 수 있다.

→ Extension. The sum of finitely many independent normals is also normal .
- Z = X + Y, X ㅛ Y, Normal (2)
- 증명(?)을 해보자.
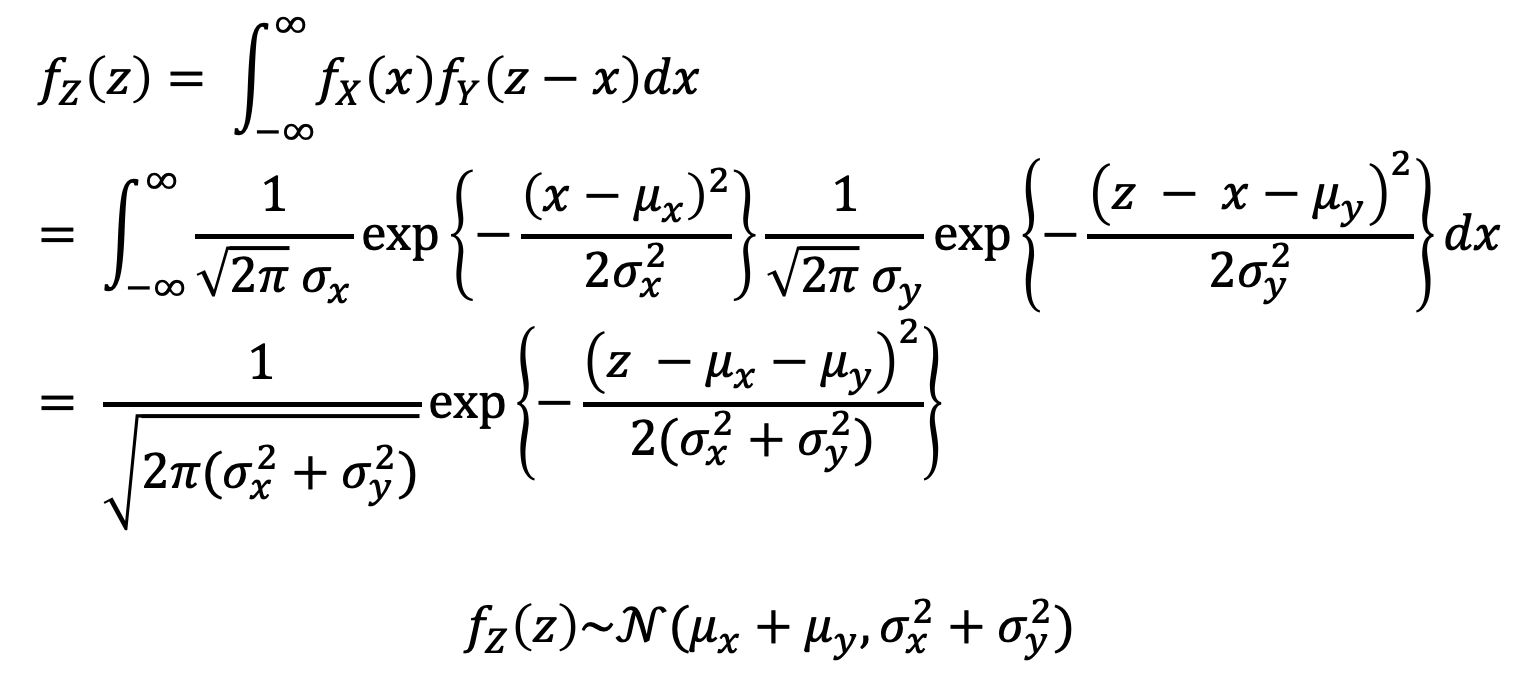
Covariance: Degree of dependence between two RVs
Making a Metric of Dependence Degree
- Goal : Given two RVs X and Y, assign some number that quantifies the degree of their dependence.
→ feeling😢 / weather⛈, university ranking / annual salary, etc…
→ Covariance : 두 개 또는 그 이상의 랜덤 변수에 대한 의존성을 의미 - Requirements
- Increase(reps. decrease) as they become more(resp. less) dependent. 0 when they are independent
- Shows the ‘direction’ of dependence by + and -.
- Always bounded by some bumber (i.e., dimensionless metric). For example, [-1, 1]
OK. Let’s design!
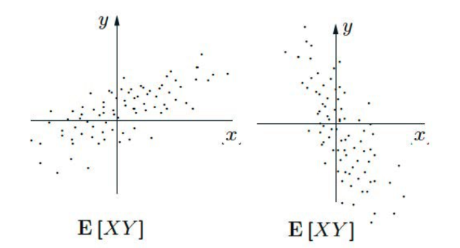
- Simple Example

- Dependent :
- Positive : if X ↑, Y ↑
- Negative : if X ↑, Y ↓
- 그럼, Covariance를 E[XY]로 표현해보자.
- E[XY] = E[X] E[Y] = 0 when X ㅛ Y
- More data points (thus increase) when xy > 0 (both positive or negative) → 서로 다르면 감소함, 즉 우리가 원하던 대로임
- | E[XY] | also quantifies the amount of spread.
What if μx != 0 and μy != 0
- Solution : Centering
→
- 이를 수식으로 사용해서 앞서 우리가 만든 공식에 대입해본다면
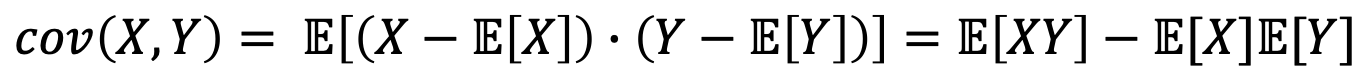
- X ㅛ Y일 때는 con(X, Y) = 0이 나온다. 즉, 독립이니까 상관이 없다는 뜻이다.
- 그럼 반대로, cov(X, Y) = 0이라해서 X ㅛ Y일까? → 항상 그렇지 않다.
- 그래서 우리는 cov(X, Y) = 0을 X와 Y가 uncorrelated하다고 부르기로 했다.
Example : cover(X, Y) = 0, but not independent.
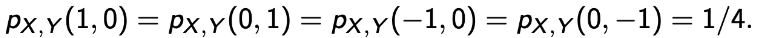
- 이렇게 된다면, E[X] = E[Y] = 0이 되고, 자연스럽게 E[XY] = 0이 되어 cov(X, Y) = 0이 된다.
- 그럼, X와 Y가 독립인가? 아니다. X(Y)가 주어졌을 때 Y(X)를 알 수 있다. 즉, 독립이 아니다.
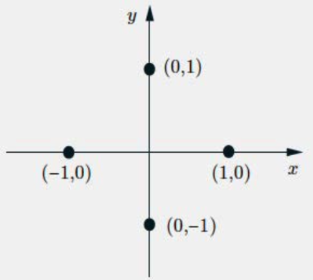
Some Properties of COV
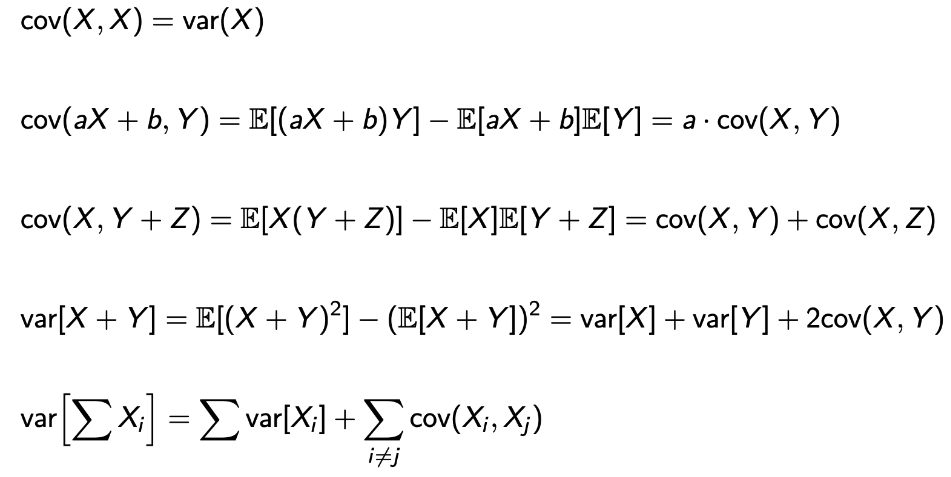
Example : The hat problem Using Bern RV
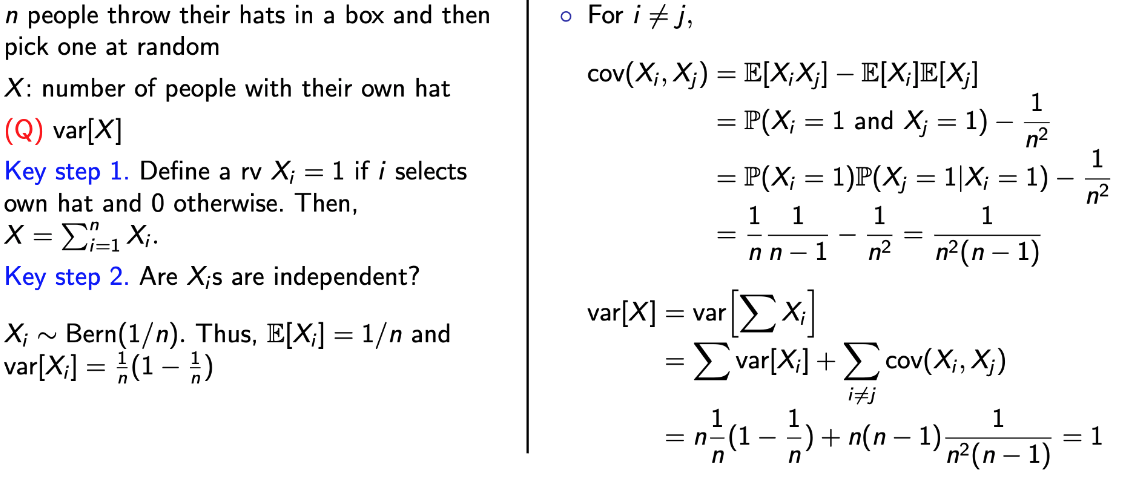
→ 앞에서 정리한 속성을 갖고 variance를 구할 수 있다.
Correlation Coefficient
-
앞서 배운 Covariance와 비슷한 내용이다. 그럼 무엇이 다를까?
-
Covariance를 만들기 위한 우리들의 요구사항#Making a Metric of Dependence Degree 을 보면 어디서 다른지 알 수 있다.
→ R1과 R2는 이미 만족을 하고 있다.
→ R3….이게 문제인데 어떻게 만족해야할까?
Bounding the metric : Correlation Coefficient
-
Normalization을 한다면 어떻게 펼쳐져있든, 일정 범위로 맞춰줄 수 있다.
-
그럼 무엇을 기준으로 해야할까?
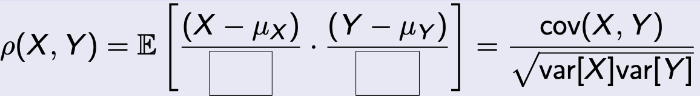
→ σ로 하면 된다.
→ 만약, 분자가 제곱의 형태를 갖는다면 → var로 하면 된다. -
식을 보자.
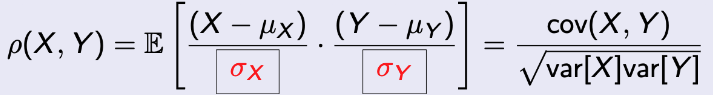
Theorem.
- 그럼, coef가 의미하는 것은 무엇일까?
- -1 <= ρ <= 1
- | ρ | = 1 ⇔ X - μX = c(Y - μY) for some constant c (c > 0 when ρ = 1 and c < 0 when ρ = -1)
→ In other words, Linear relation meaning VERY RELATED.
Proof. 1

Proof. 2
