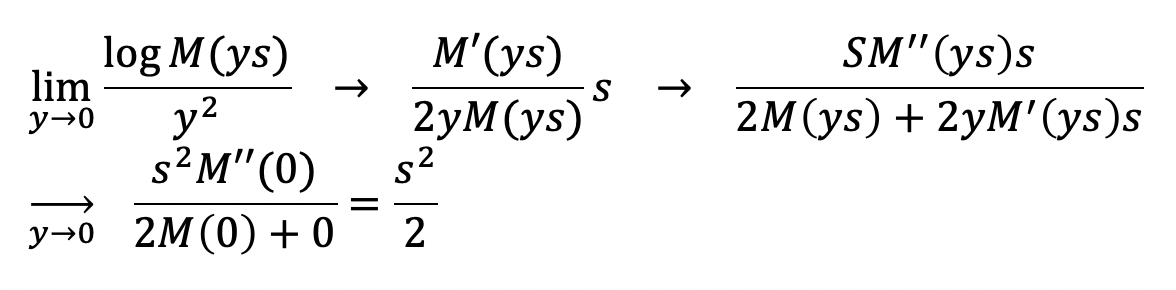Random Variables (9)
Random Variable (9)
현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.
Weak Law of Large Numbers : Proof
- WLLN을 증명하기 위해서 Inequality에 관한 두 가지 증명을 알아야 한다.
- Markov Inequality
- Chebyshev Inequality
- 하나씩 증명해보자.
Markov Inequality
- 이 증명이 궁금해 하는 질문은
→ Knowing E(X), Can we say something about the distribution of X? - E만 알고 있다고 해서, distribution을 정확히 알 수는 없지만 rough하게는 알 수 있다.
- 직관적으로 생각해보자.
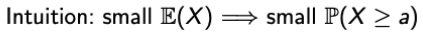
- 이를 활용한 것이 Markov Inequality이다.

- 이제 이를 증명해보자. 간단하다.
- a > 0일 때, Ya라는 RV를 하나 정의하자.
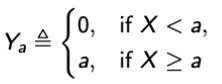
- 그러면, non-negativity of X를 사용해서 Ya <= X일 때, E[Ya] <= E[X]임을 알 수 있다.
- 이제 마지막 단계!
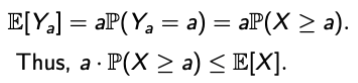
- a > 0일 때, Ya라는 RV를 하나 정의하자.
Chebyshev Inequality
- 이 증명도 궁금해하는 것이 있다.
→ Knowing both E(X) and var(X), Can we say something about the distribution of X? - Markov Inequality보다 주어진 정보가 더 많으니, 이보다 조금이라도 더 자세하게 distribution을 표현할 수 있을 것이다.
- 직관적으로 생각해보자.
→ 작은 분산은 무엇을 의미할까? 즉, small var(X)가 무엇을 의미할까?
→ 간단하게, X가 이것의 평균으로부터 멀지 않은 곳에 뭉쳐있음을 의미한다 (간단). - 자 그러면, Expectation이 μ, Var가 σ^2이라고 해보자.
→ 이러한 가정에서 Chebyshev Inequality는 다음을 정의한다.
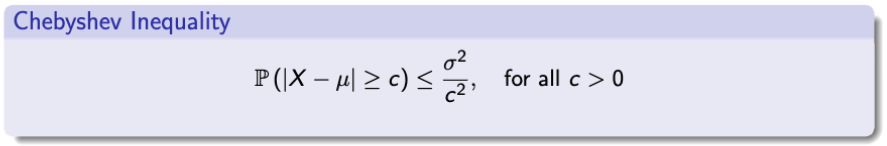
- 정의는 더 간단하다.
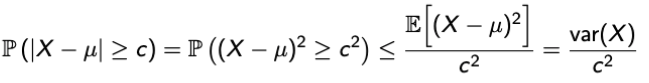
Example: MI vs CI
-
먼저 앞서 증명한 MI와 CI는 정확한 Distribution이 아닌, 여기 정도에 존재할 것 같다라는 bound를 제공한다.
- X ~ exp(1). Then, E[X] = 1/λ = 1, Var[X] = 1/(λ^2) = 1
- Exact CCDF : P(X >= a) = e^(-aλ) = e^(-a)
| Markov Inequality | Chebyshev Inequality |
|---|---|
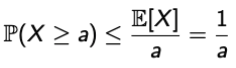 |
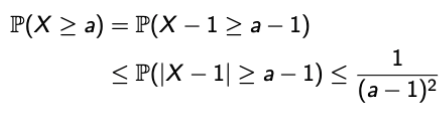 |
- 여기서 알아낼 수 있는 것은 무엇일까?
- For resonably large a, CI provides much better bound.
- Knowing the variance helps
- Both bounds are the ones that bound the probability of rare events.
Back to WLLN Proof
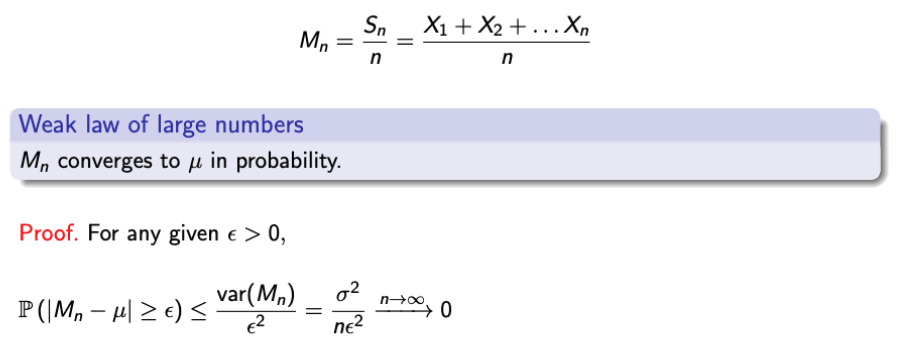
- CI를 적용하면 다음과 같이 정의할 수 있다.
Comparison : WLLN vs CLT
- 동일한 문제에 대해서 WLLN과 CLT로 풀었을 때의 차이점을 확인해보자.
Example : Polling using WLLN
-
p : fraction of voters who support someone
-
Interview n randomly selected voters and record the result in Mn = (X1 + … + Xn)/n which is a estimate of p, where Bern. rv Xi = 1 if i-th interviewee answers ‘yes’, and 0 otherwise.
-
그러면 다음과 같이 WLLN과 CI를 사용하여 식을 만들 수 있다.
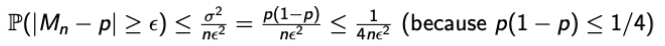
Q1. What is n so that the probability that our estimate is correct by more than 0.1 is no longer than 0.25?
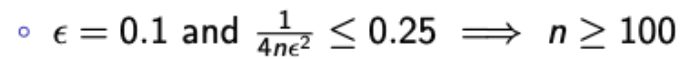
Q2. What is n so that the probability that our estimate is correct by more than 0.01 is no longer than 0.05?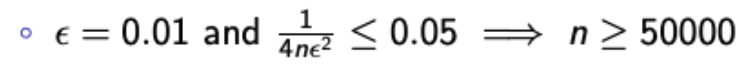
Example : Polling using CLT
-
조건은 이전에 푼 문제와 동일하다.
-
그러면, 이번엔 CLT를 적용해서 식을 만들어보자.
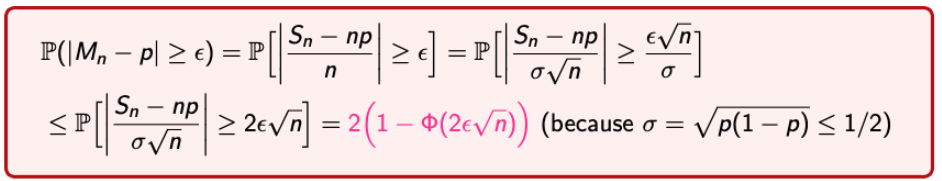
-
WLLN에서 풀었던 두번째 질문에 대해 CLT를 사용해서 답을 도출해보자.
Central Limit Theorem: Proof
Moment Generating Function (MGF)
- CLT에 대한 증명을 하기 전에 MGF라는 것을 알고 가보자
- 간단하게 Moment Generating Function은 s라는 파라미터를 갖는 X에 대한 함수이다.
→ The Moment Generating Function Mx(s) of a rv X is a function of a scaler parameter s - 수식으로는 다음과 같이 표현된다.
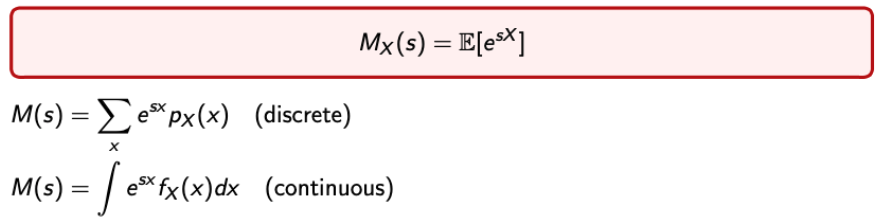
- 정리할 때는 편하게 M(s)라고 적겠다.
Examles
- 몇 가지의 예제를 통해 MGF를 만드는 법을 확인해보자.
- Discrete
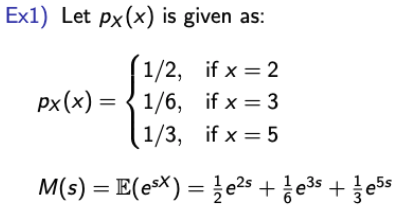
- Continuous
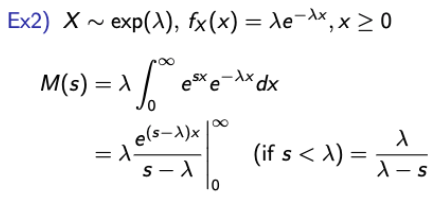
- Linear RVs
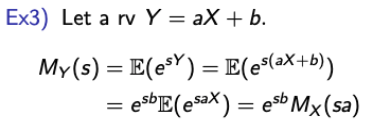
→ MY와 MX간의 관계를 표현하는 식으로도 해석이 가능하다. - Standard Noraml RV
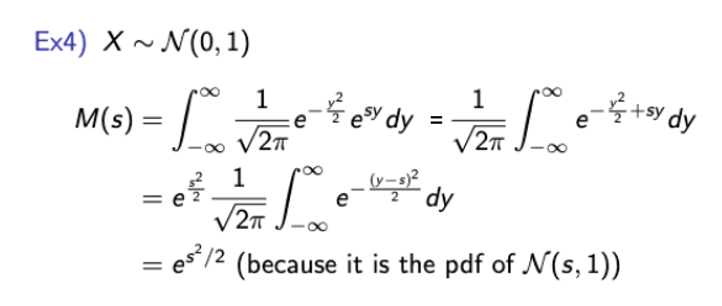
- Discrete
Useful Properties of MGF

Example
- 앞서 설명한 속성이 어떻게 활용되는지 간단한 Exp RV를 통해 이해해보자.
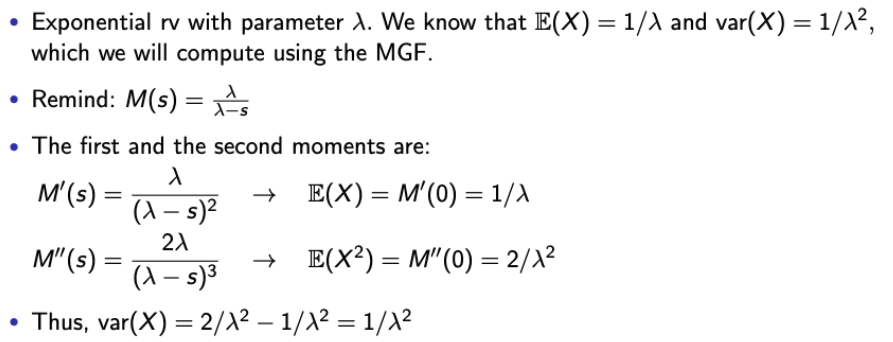
Inversion Property
- MGF에는 또 다른 중요한 특성이 있다.

- 이게 무슨 말일까?
→ 간단히 말하자면, MGF와 X는 일대일 관계이고, 만약 우리가 MGF를 안다면 distribution을 recover 할 수 있다는 것이다. - 어떨 떄는 복구하는 것이 어려울 수도 있고, 쉬울 수도 있다.
- 쉬운 예제와 어려운 예제를 하나씩 살펴보자.
Example 1.
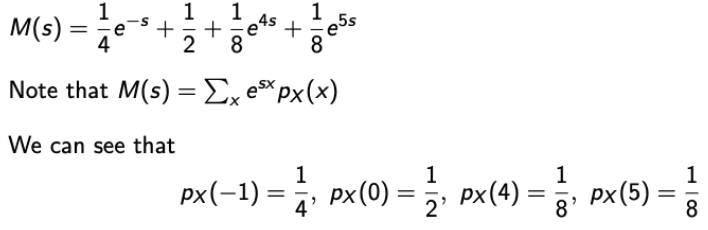
→ 쉽다 쉬워~~~ 이제 어려운거 해보자.
Example 2.

→ 식을 전개하면서 사용한 방법은 1 + a + a^2 + … = 1/(1-a) (when abs(a) < 1)
Back to CLT Proof
- Without loss of generality, assume E(Xi) = 0 and var(Xi) = 1.
- 그러면 Zn은 다음과 같이 정의가 될 것이다.
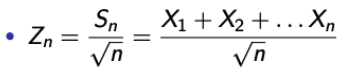
- 먼저, Zn의 MGF를 구해보자. (이는 Standard Normal Distribution이 될 것이다.)
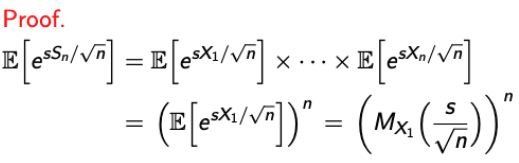
- 간단하게 수식을 전개하기 위해 M = M_X1이라고 하자.
- 그럼 우리가 배웠던 MGF의 첫번째 속성에 의해 다음을 알 수 있다.
→ M(0) = 1, M’(0) = 0, M’‘(0) = 1 - 그리고 우리가 CLT의 증명을 위해 원하는 것은 다음이다.
→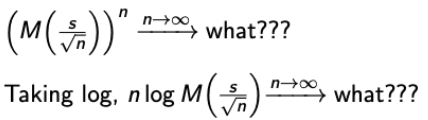
→ 증명을 위해 log도 취하겠다. (으 취한다) - 그리고 더 편리함을 위해 y = 1/sqrt(n)이라고 하면
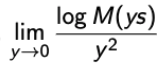
→ 분모가 0으로 수렴하니까, 로피탈 룰을 2번 적용하자.